Кинетическая энергия пружины

Механическая энергия

Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.

Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.

Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим ), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.

Кинетическая энергия

Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.

Кинетическая энергия Ек — кинетическая энергия m — масса тела v — скорость [м/с]

Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.

Задачка раз

Определить кинетическую энергию собаченьки массой 10 кг, если она бежала за мячом с постоянной скоростью 2 м/с.

Решение:

Формула кинетической энергии

Подставляем значения

Дж

Ответ: кинетическая энергия пёсы равна 20 Дж.

Задачка два

Найти скорость бегущего по опушке гнома, если его масса равна 20 кг, а его кинетическая энергия — 40 Дж

Решение:

Формула кинетической энергии

Выразим скорость:

Подставляем значения

Ответ: гном бежал со скоростью 2 м/с.

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

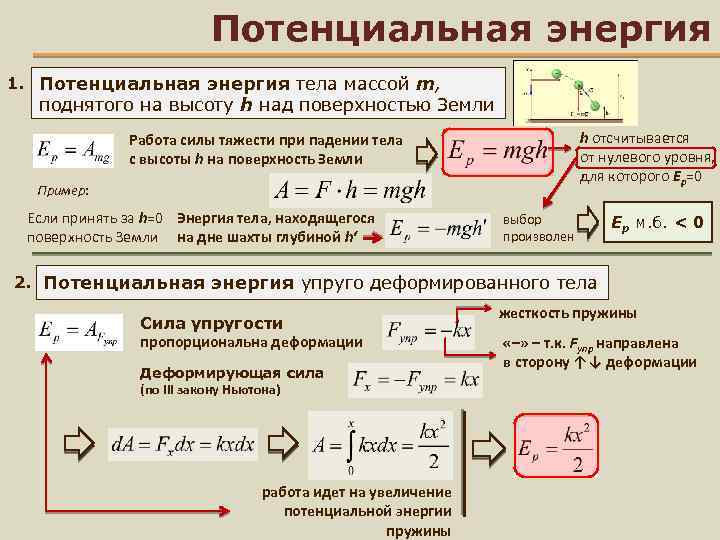
Потенциальная энергия

В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.

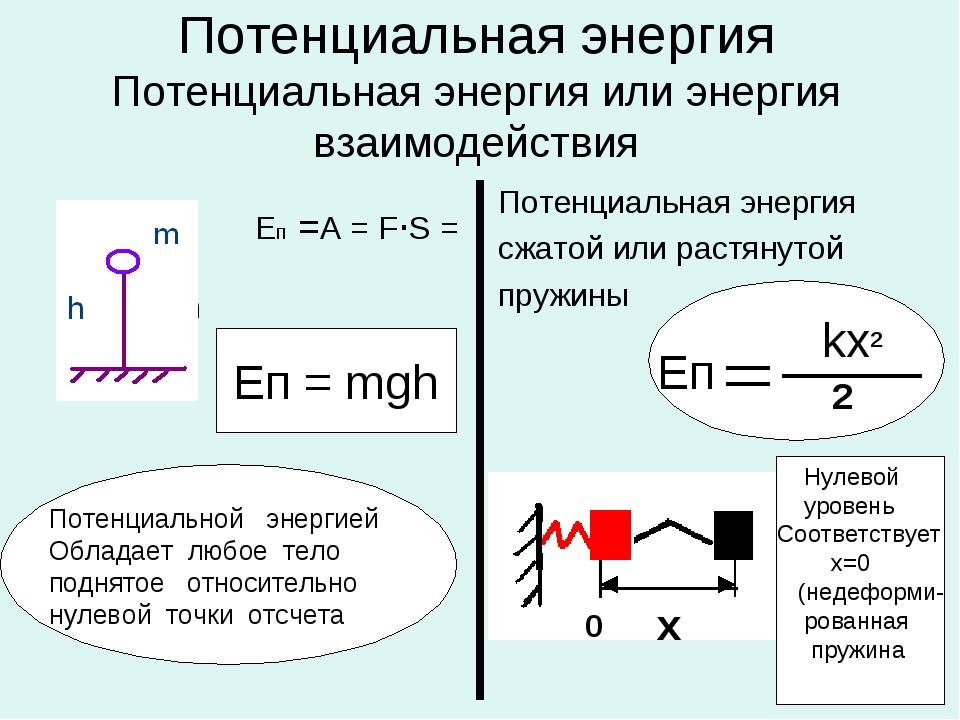
Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.

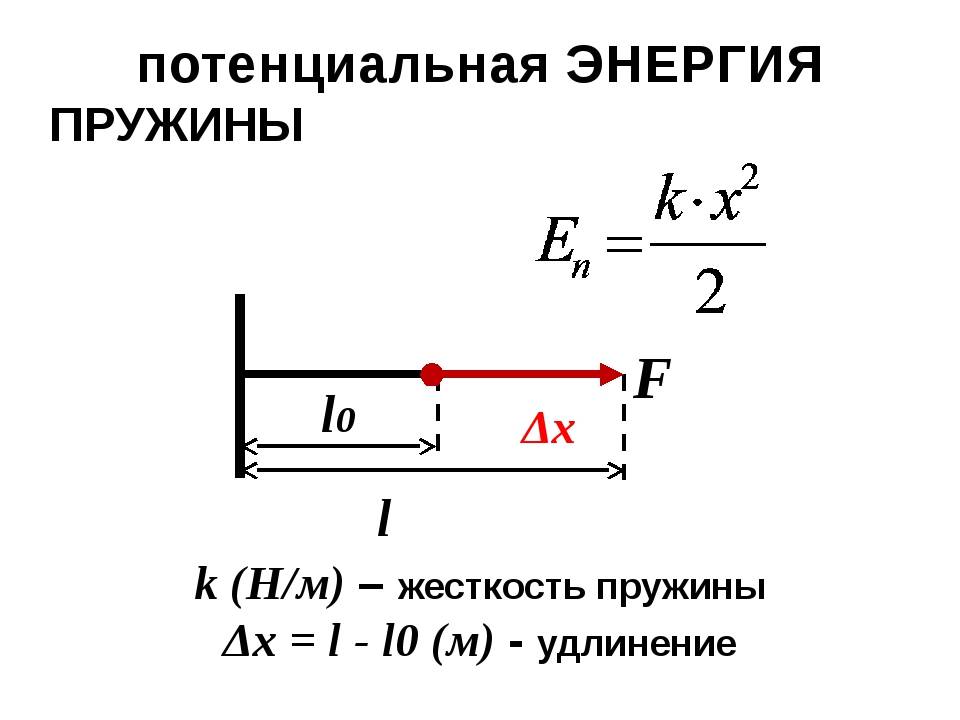
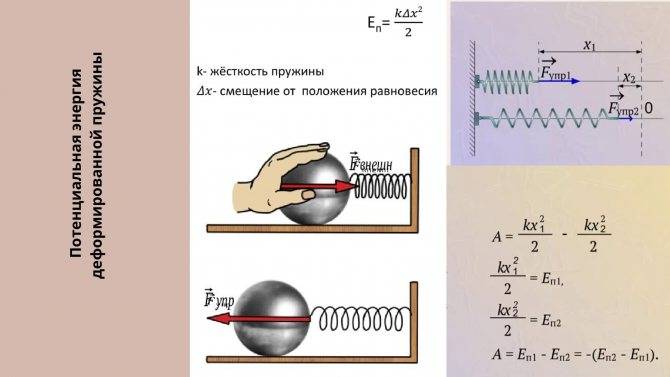
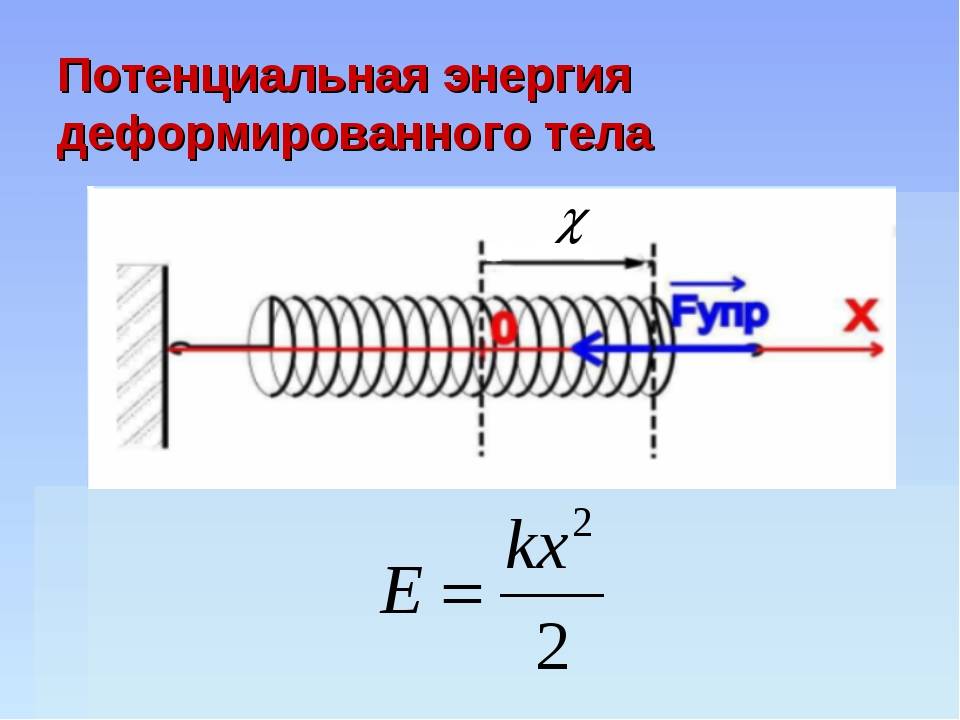
Потенциальная энергия деформированной пружины Еп — потенциальная энергия k — жесткость [Н/м] x — удлинение пружины

Потенциальная энергия в поле тяжести Еп = mgh Еп — потенциальная энергия m — масса тела g — ускорение свободного падения [м/с2] h — высота На планете Земля g ≃ 9,8 м/с2

Задачка раз

Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с2.

Решение:

Формула потенциальной энергии Е_п = mgh

Подставляем значения

E_п = 0,1 · 9,8 · 2500 = 2450 Дж

Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.

Задачка два

Найти высоту горки, с которой собирается скатиться лыжник массой 65 кг, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с2.

Решение:

Формула потенциальной энергии Е_п = mgh

Выразим высоту:

Переведем 637 кДж в Джоули.

637 кДж = 637000 Дж

Подставляем значения

м

Ответ: высота горы равна 1000 метров.

Задачка три

Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E₁ и E₂. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.

Решение:

Потенциальная энергия вычисляется по формуле: E = mgh

По условию задачи

m₁ = m

h₁ = 2h

m₂ = 2m

h₂ = h

Таким образом, получим, что

E₁ = mg2h = 2mgh,

а E₂ = 2mgh,

то есть E₁ = E₂.

Ответ: E₁ = E₂.

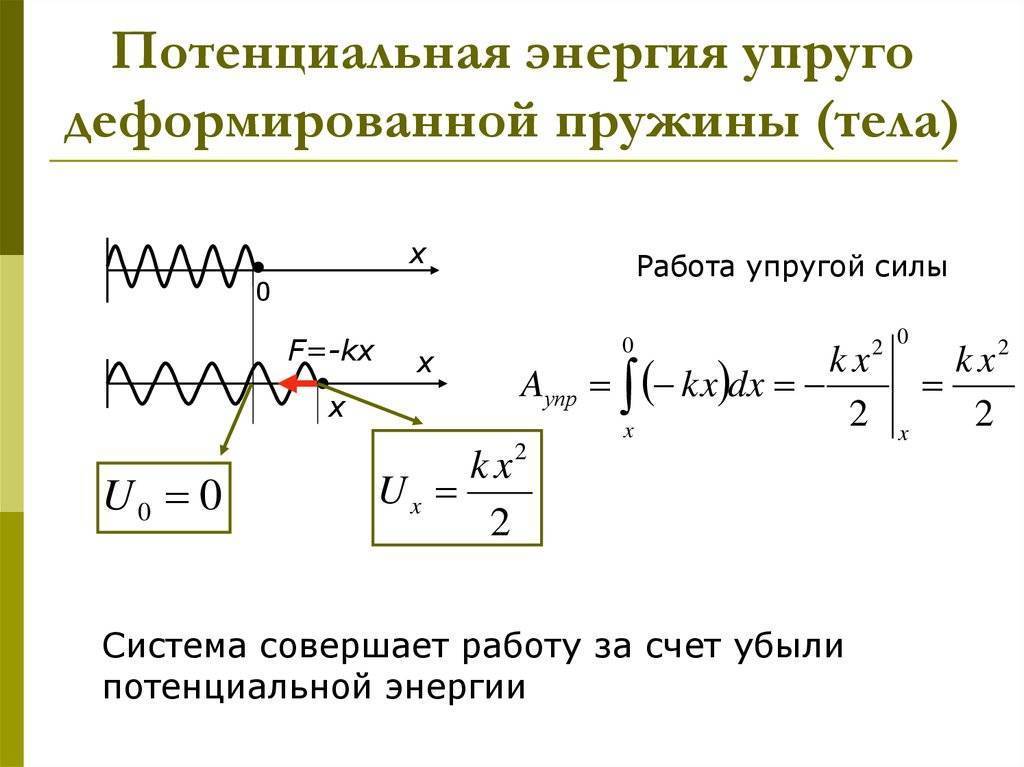
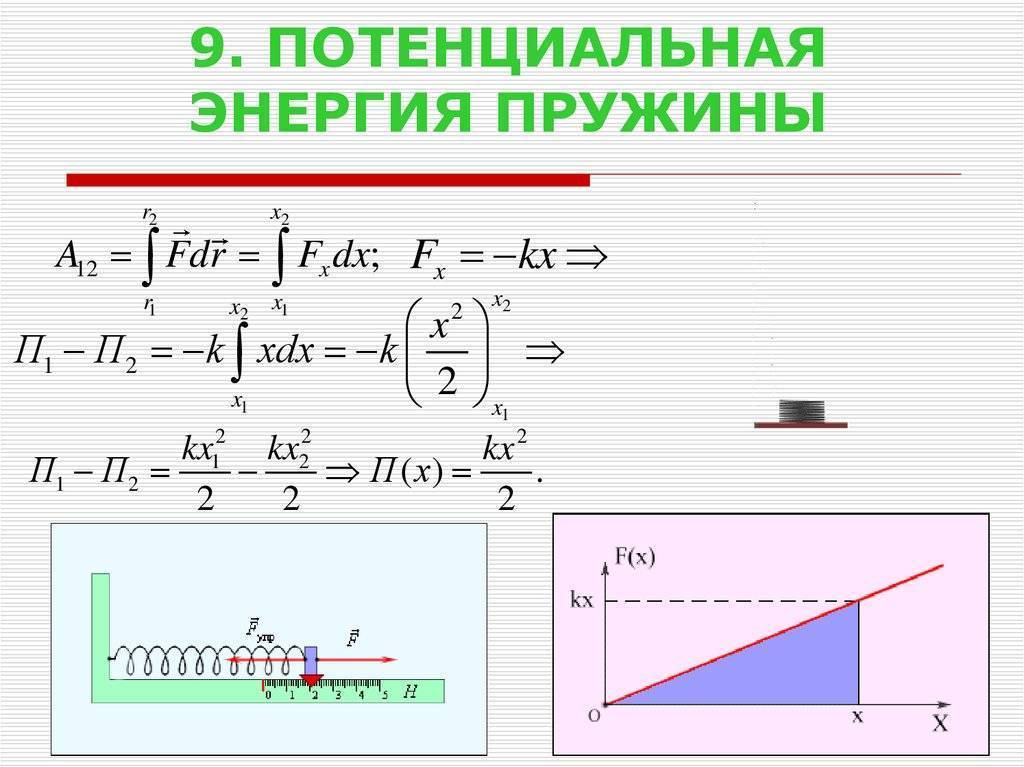
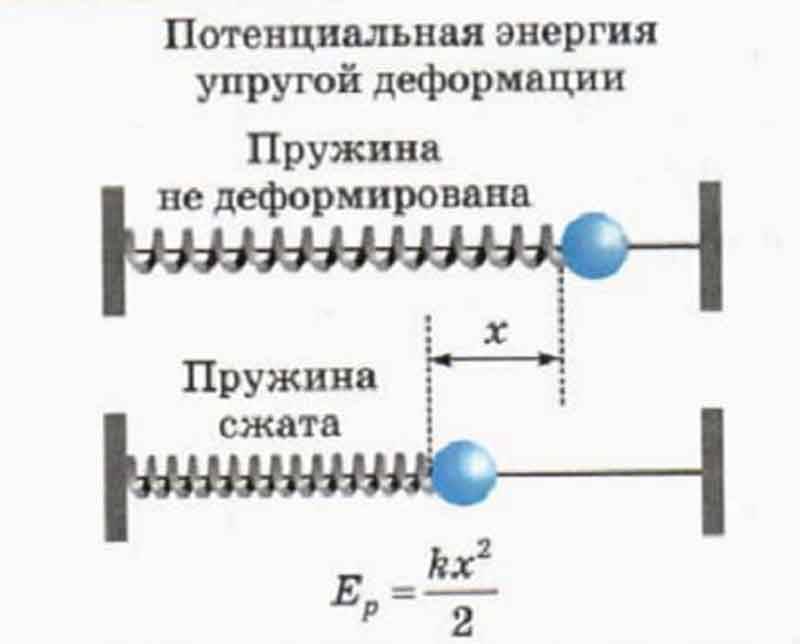
Потенциальная энергия сжатой или растянутой пружины

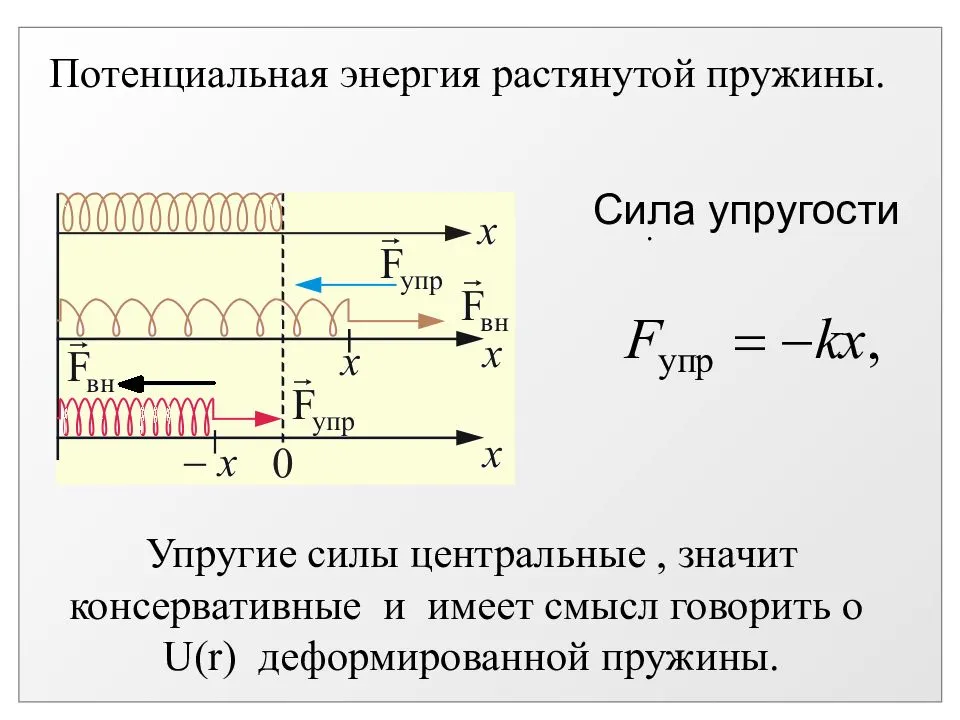
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) ) – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.

Сила упругости в пружинном маятнике

Следует учитывать тот момент, что до деформирования пружины она находится в положении равновесия. Приложенная сила может приводить к ее растягиванию и сжиманию. Сила упругости в пружинном маятнике рассчитывается в соответствии с тем, как воздействует закон сохранения энергии. Согласно принятым нормам возникающая упругость пропорциональна смещению тела. В этом случае кинетическая энергия рассчитывается по формуле: F=-kx. В данном случае применяется коэффициент жесткости пружины.

Выделяют довольно большое количество особенностей воздействия силы упругости в пружинном маятнике. Среди особенностей отметим:

1. Максимальная сила упругости возникает на момент, когда тело находится на максимальном расстоянии от положения равновесия. При этом в подобном положении отмечается максимальное значение ускорение тела. Не следует забывать о том, что может проводится растягивание и сжатие пружины, оба варианта несколько отличается. При сжатии минимальная длина изделия ограничивается. Как правило, она имеет длину, равную диаметру витка умноженное на количество. Слишком большое усилие может стать причиной смещения витков, а также деформации проволоки. При растяжении есть момент удлинения, после которого происходит деформация. Сильное удлинение приводит к тому, что возникающей силы упругости недостаточно для возврата изделия в первоначальное состояние.
2. При сближении тела к месту равновесия происходит существенное уменьшение длины пружины. За счет этого наблюдается постоянное снижение показателя ускорения. Все это происходит за счет воздействия усилия упругости, которая связано с типом применяемого материала при изготовлении пружины и ее особенностями. Длина уменьшается за счет того, что расстояние между витками снижается. Особенностью можно назвать равномерное распределение витков, лишь только в случае дефектов есть вероятность нарушения подобного правила.
3. На момент достижения точки равновесия сила упругости снижается до нуля. Однако, скорость не снижается, так как тело движется по инерции. Точка равновесия характеризуется тем, что длина изделия в ней сохраняется на протяжении длительного периода при условии отсутствия внешнего деформирующего усилия. Точка равновесия определяется в случае построения схемы.
4. После достижения точки равновесия возникающая упругость начинает снижать скорость перемещения тела. Она действует в противоположном направлении. При этом возникает усилие, которое направлено в обратную сторону.
5. Дойдя крайней точки тело начинает двигаться в противоположную сторону. В зависимости от жесткости установленной пружины подобное действие будет повторятся неоднократно. Протяженность этого цикла зависит от самых различных моментов. Примером можно назвать массу тела, а также максимальное приложенное усилие для возникновения деформации. В некоторых случаях колебательные движения практически незаметны, но они все же возникают.

Приведенная выше информация указывает на то, что колебательные движения совершаются за счет воздействия упругости. Деформация происходит за счет приложенного усилия, которое может варьировать в достаточно большом диапазоне, все зависит от конкретного случая.

Средняя кинетическая энергия

В большинстве случаев проводится высчитывание среднего значения. Этот показатель не учитывает то, в каких положениях сила упругости высокая и низкая. Для расчета применяется формула: F=kl/2.

В данном случае достаточно знать лишь удлинение, которое измеряется при использовании обычного инструмента. Что касается коэффициента, то он может варьировать в достаточно большом диапазоне, зависит от следующих моментов:

1. Диаметра витков. С увеличением этого показателя существенно повышается коэффициент жесткости, изделие часто используется для выполнения большой работы.
2. Толщины применяемой проволоки. Рассматриваемое изделие представлено проволокой, которая накручивается вокруг установленной оси.
3. Расстояния между отдельными витками. Как правило, они расположены относительно друг друга на определенном расстоянии, которое одинаковое. По этому признаку выделяют варианты исполнения, предназначенные для сжатия и растяжения.
4. Типа применяемого материала при изготовлении. Некоторые сплавы характеризуются достаточно высокой жесткостью, могут переносить незначительную деформацию.

Коэффициент самостоятельно рассчитать не нужно, он берется с определенных таблиц. Среднее значение часто высчитывается в случае решения математических задач, при проектировании применяются другие формулы.

Потенциальная энергия

Кинетическая энергия — это энергия движения. Наряду с кинетической энергией есть еще потенциальная энергия, то есть энергия взаимодействия тел, которая зависит от их положения.

Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциальная энергия. Когда тело падает вниз под действием силы тяжести, эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.

Вообще о потенциальной энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными (или диссипативными).

Примеры диссипативных сил: сила тяжести, сила упругости.

Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.

Рассмотрим пример, когда шар переместился из точки с высотой h 1 в точку с высотой h 2 .

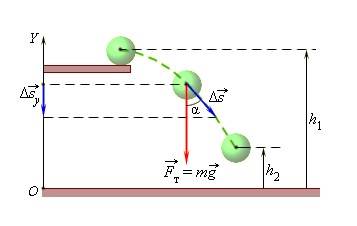
При этом сила тяжести совершила работу, равную

A = — m g ( h 2 — h 1 ) = — ( m g h 2 — m g h 1 ) .

Эта работа равна изменению величины m g h , взятому с противоположным знаком.

Величина Е П = m g h — потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальная энергия тела равна нулю.

Определение. Потенциальная энергия

Потенциальная энергия — часть полной механической энергии системы, находящейся в поле диссипативных(консервативных) сил. Потенциальная энергия зависит от положения точек, составляющих систему.

Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины и т.д.

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

A = — ( E П 2 — E П 1 ) .

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела

Здесь G — гравитационная постоянная, M — масса Земли.

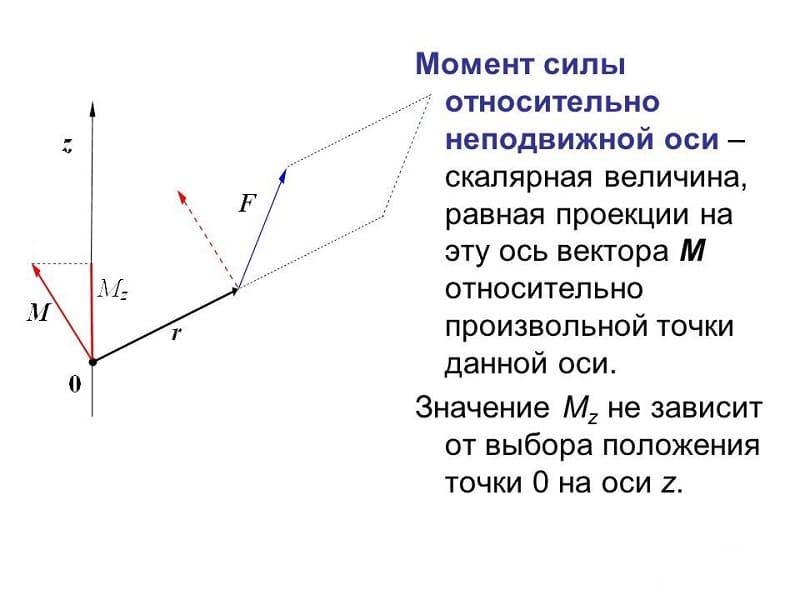
Момент силы и момент импульса относительно оси

Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.

Момент импульса – величина, которая применяется для определения количества вращательного движения.

Среди особенностей подобного показателя можно отметить следующее:

1. Масса вращения. Объект может характеризоваться различной массой.
2. Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
3. Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.

Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.

Максимальная кинетическая энергия груза на пружине

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

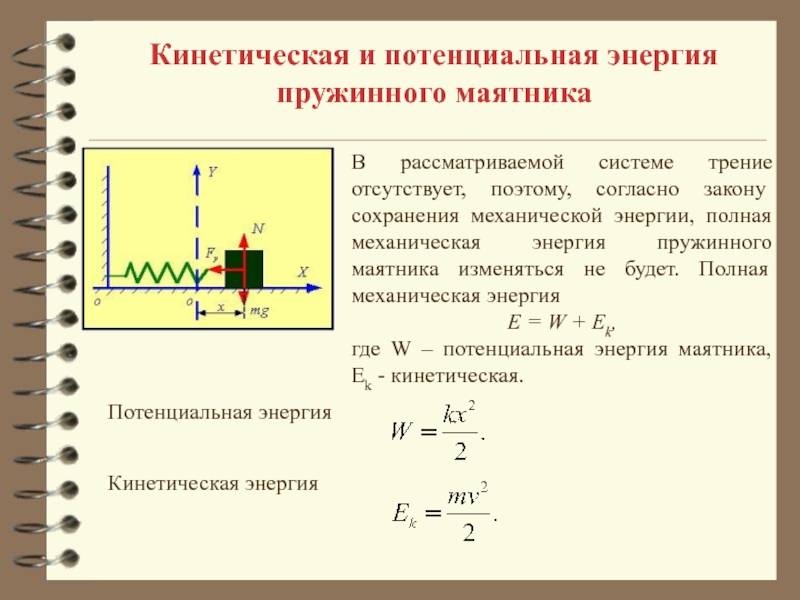
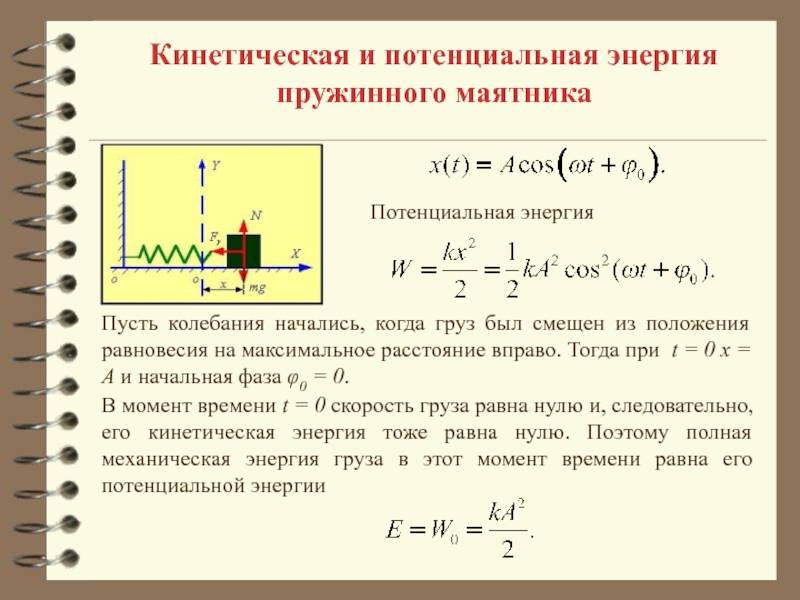
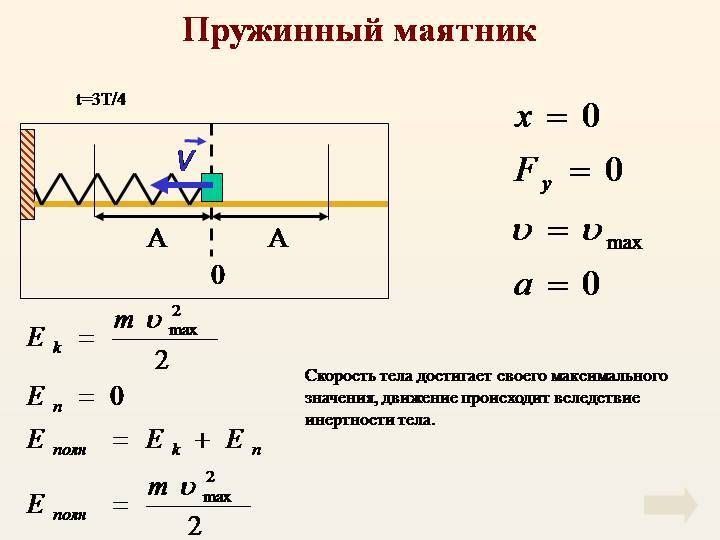
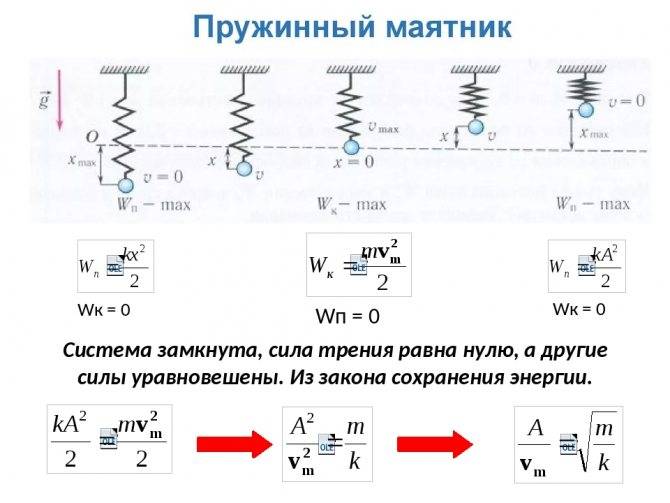
При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени

Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле

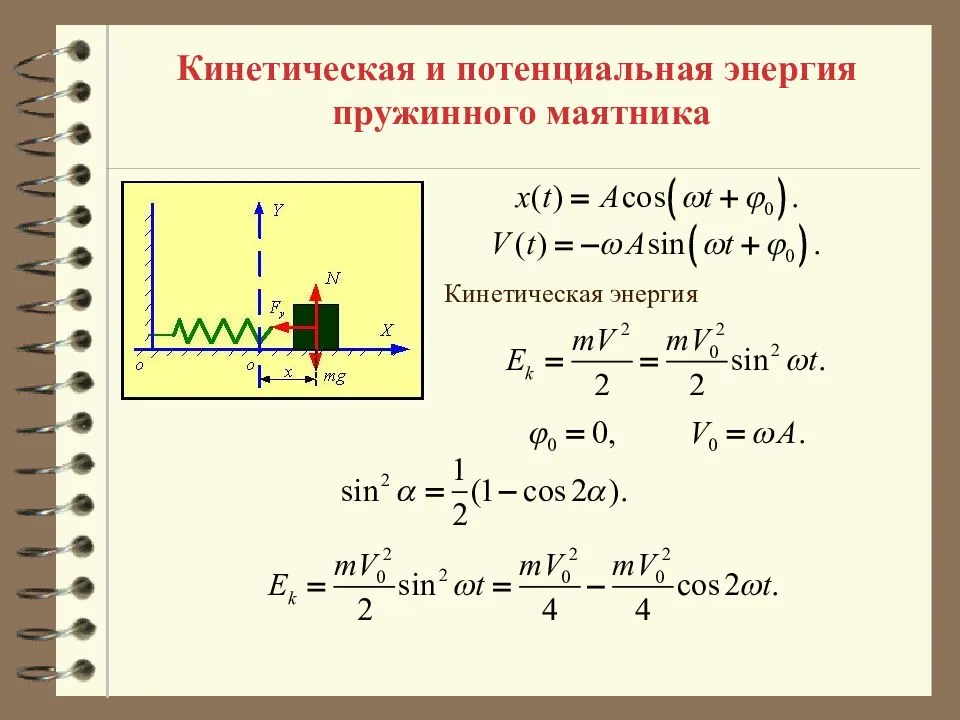
Б) Для пружинного маятника известны формулы кинетической энергии

Пру­жин­ный ма­ят­ник, со­сто­я­щий из груза и лёгкой пру­жи­ны, со­вер­ша­ет ко­ле­ба­ния. В мо­мент, когда груз на­хо­дит­ся в край­нем по­ло­же­нии, его не­мно­го под­тал­ки­ва­ют вдоль оси пру­жи­ны в на­прав­ле­нии от по­ло­же­ния

рав­но­ве­сия. Как в ре­зуль­та­те этого из­ме­ня­ют­ся мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка и ча­сто­та его ко­ле­ба­ний?

Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

3) не из­ме­ня­ет­ся

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

Мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка

Ча­сто­та ко­ле­ба­ний ма­ят­ни­ка

Груз под­толк­ну­ли от по­ло­же­ния рав­но­ве­сия, от­ку­да сле­ду­ет, что ам­пли­ту­да ко­ле­ба­ний груза уве­ли­чит­ся. При этом уве­ли­чит­ся также и мак­си­маль­ная по­тен­ци­аль­ная энер­гия пру­жи­ны. По за­ко­ну со­хра­не­ния энер­гии, это при­ве­дет к уве­ли­че­нию мак­си­маль­ной ки­не­ти­че­ской энер­гии груза ма­ят­ни­ка.

Пе­ри­од и ча­сто­та пру­жин­но­го ма­ят­ни­ка за­ви­сят толь­ко от массы груза и жест­ко­сти пру­жи­ны. Таким об­ра­зом, при уве­ли­че­нии ам­пли­ту­ды ко­ле­ба­ний груза, ча­сто­та ко­ле­ба­ний ма­ят­ни­ка не из­ме­нит­ся.

Формула потенциальной энергии

О потенциальной энергии деформированной механической системы мы обязательно поговорим. Но как-нибудь далее в курсе физики. Для начала нужен ряд определений для механики деформации. Так что пока остановимся на потенциальной энергии под действием знакомой нам силы — силы тяжести.

Если взять за ноль потенциальную энергию точки, находящейся на земле, то потенциальная энергия точки, находящейся на некотором расстоянии от земли, определяется работой, которая выполнится гравитационной силой при падении.

Договоримся обозначать такую потенциальную энергию как $E_П$

Далее вспомним важное условие:. Следовательно $A=\Delta{E_п}$

Помним, что работа равна произведению значения силы на пройденный путь, $A=F\cdot s$. Теперь формула потенциальной энергии в шаге от готовности, если вспомнить, что $F=ma$. Под силой сейчас понимается конкретная сила — сила тяжести $mg$. Тогда заметим, что:

Следовательно $A=\Delta{E_п}$. Помним, что работа равна произведению значения силы на пройденный путь, $A=F\cdot s$. Теперь формула потенциальной энергии в шаге от готовности, если вспомнить, что $F=ma$. Под силой сейчас понимается конкретная сила — сила тяжести $mg$. Тогда заметим, что:

$A=mg\cdot s$.

Но это еще не конечный вариант того, как выглядит формула потенциальной энергии. Пройденный путь $s$ имеет немного другое прочтение, когда речь идет о гравитационном притяжении. Раз мы говорим прежде всего о падении, путь такой работы — высота, на которую было поднято тело.

Получается, что формула потенциальной энергии, с учетом всех моментов, выглядит так:

$$A=\Delta{E_п}=mgh,$$

где $m$ — масса тела, $h$ — высота подъема, $g$ — ускорение свободного падения.

Как найти высоту потенциальной энергии

«Высота подъема» — формулировка условная. Еще ее часто определяют в справочной литературе как «высота от центра тяжести до Земли». Дадим этому разъяснение.

Для примера рассмотрим следующую конструкцию. Пусть есть стол, на котором лежит коробка, на верху которой, в свою очередь, расположен предмет — кастрюля. Итого, как найти высоту потенциальной энергии кастрюли?

Высота потенциальной энергии может быть определена относительно стола. Или относительно пола. Может быть, уровня земли, если стол расположен внутри здания. Относительно подвала? Иными словами, подъем тела рассчитывается относительно чего угодно. Выходит, нужно всегда заранее условиться, относительно какого уровня производится замер.

Однако помните, что именно «условиться» — выбрать точку отсчета можно произвольно. Чтобы она была максимально удобная для расчетов. Намного важнее — величина изменения потенциальной энергии, а совсем не то, как найти высоту потенциальной энергии. Очевидно, вне зависимости от выбранной точки отсчета, изменение потенциальной энергии будет одним и тем же.

Еще немаловажен фактор центра тяжести. Если тело маленькое и располагается на поверхности «земли», говорят, что его потенциальная энергия равна нулю. Расстоянием от центра тяжести до нулевого уровня можно пренебречь. Другое дело, когда тело габаритное.

Обратите внимание на изображение. Несмотря на то, что крупный предмет находится на нулевом уровне, его потенциальная энергия больше нуля

В общей сложности, важнее не вопрос «как найти высоту потенциальной энергии», ибо он не конкретен. Важнее вопрос — какую точку отсчета выбрать?

Физическая размерность

В системе физических величин LMT энергия имеет размерность M L 2 T − 2 {\displaystyle ML^{2}T^{-2}} . Соотношения между единицами энергии.

Единица	Эквивалент
в	в эрг	в межд. кал	в
1	1	107	0,238846	0,624146·1019
1 эрг	10−7	1	2,38846·10−8	0,624146·1012
1 межд. Дж	1,00020	1,00020·107	0,238891	0,624332·1019
1 кгс·м	9,80665	9,80665·107	2,34227	6,12078·1019
1 кВт·ч	3,60000·106	3,60000·1013	8,5985·105	2,24693·1025
1 ·атм	101,3278	1,013278·109	24,2017	63,24333·1019
1 межд. кал (calIT)	4,1868	4,1868·107	1	2,58287·1019
1 термохим. кал (калТХ)	4,18400	4,18400·107	0,99933	2,58143·1019
1 электронвольт (эВ)	1,60219·10−19	1,60219·10−12	3,92677·10−20	1

Формула для расчета периода колебаний пружинного маятника

• Механика (56)
  • Кинематика (19)
  • Динамика и статика (32)
  • Гидростатика (5)
• Молекулярная физика (25)
  • Уравнение состояния (3)
  • Термодинамика (15)
  • Броуновское движение (6)
  • Прочие формулы по молекулярной физике (1)
• Колебания и волны (22)
• Оптика (9)
  • Геометрическая оптика (3)
  • Физическая оптика (5)
  • Волновая оптика (1)
• Электричество (39)
• Атомная физика (15)
• Ядерная физика (3)

• Квадратный корень, рациональные переходы (1)
• Квадратный трехчлен (1)
• Координатный метод в стереометрии (1)
• Логарифмы (1)
• Логарифмы, рациональные переходы (1)
• Модуль (1)
• Модуль, рациональные переходы (1)
• Планиметрия (1)
• Прогрессии (1)
• Производная функции (1)
• Степени и корни (1)
• Стереометрия (1)
• Тригонометрия (1)
• Формулы сокращенного умножения (1)

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке! Жмите СЮДА

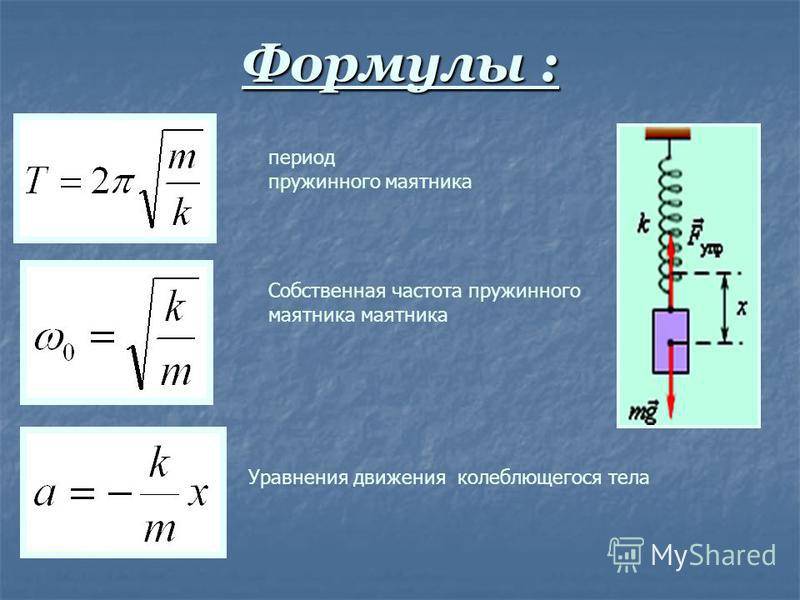
Период пружинного маятника — зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается

Пружинный маятник — это груз, колеблющийся на пружине. Он совершает возвратно-поступательное движение. Пружинный маятник подчиняется законам движения, по которым можно определить период его колебаний, зная массу груза и жесткость пружины. Период колебаний пружинного маятника не зависит от места его расположения и амплитуды колебаний.

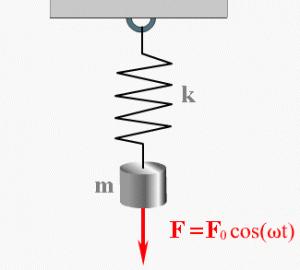
Давайте выведем формулу периода пружинного маятника.

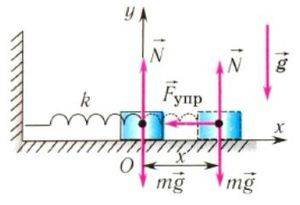
На груз m горизонтального пружинного маятника действуют сила тяжести (mg), сила реакции опоры (N) и сила упругости пружины (Fynp). Запишем второй закон Ньютона для данного случая :

Все проецируем на ось ОХ:

Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора:

Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:

Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:

Тогда период колебаний пружинного маятника будет равен:

• Период физического маятника
• Период крутильного маятника
• В Формуле мы использовали :
• — Период пружинного маятника маятника
• — Масса груза
• — Изменение длины пружины
• — Коэффициент упругости пружины
• — Ускорение свободного падения
• — Циклическая частота пружинного маятника
• — Сила реакции опоры
• — Сила упругости

Формула периода колебаний пружинного маятника

1. Период — это минимальное время, за которое совершается одно полное колебательное движение.
2. Обозначают период буквой $T$.
3. где $Delta t$ — время колебаний; $N$ — число полных колебаний.

Уравнение колебаний пружинного маятника

Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k $(рис.1).

Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести.

Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:

• Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:
• Ускорение груза запишем, помня, что движение происходит по оси X, как:
• Второй закон Ньютона для груза принимает вид:
• Учтем равенство (2), формулу (5) преобразуем к виду:
• Если ввести обозначение: $^2_0=frac$, то уравнение колебаний запишем как:
• где $^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:
• где $_0=sqrt>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; $_0t+varphi )$ — фаза колебаний; $varphi $ и $_1$ — начальные фазы колебаний.

Энергия кинетическая: формула и определение

Механическая система, которая связана со скоростью перемещения объекта, применяется крайне часто. Стоит учитывать, что она может делиться на поступательную и вращательную. В качестве единицы измерения используется джоуль.

https://youtube.com/watch?v=xrK08SCiXTQ

Среди особенностей отметим нижеприведенные моменты:

1. Рассматриваемый тип усилия также представлен разностью между исходным состоянием тела и его положением в полном спокойствии.
2. Обуславливается возникновение определенного усилия, за счет которого обеспечивается перемещение тела и совершение работы.

Пружина за счет силы упругости приводит в движение различные объекты. При этом жесткость пружины растянутой может быть различной, все зависит от особенностей конкретного изделия.

Рассматриваемая формулу следует уделить внимание достаточно большому количеству различных моментов. Особенностями назовем следующее:

Упругость зависит от количества витков, толщины применяемой проволоки и типа применяемого материала при изготовлении

Кроме этого, уделяется внимание взаимному расположению витков.
Работа, которая может совершаться пружиной, зависит от взаимного положения частей тела. Начальное и конечное растяжение может существенно отличаться.
Рассматриваемое изделие в растянутом положении может совершать различную работу

Расчеты позволяют определить то, каково ее значение, а также величину потенциальной.

Расчеты могут проводится исключительно после создания схемы. Примером назовем следующее:

1. Один конец витков закреплен за основание, второй предназначен для совершения работы.
2. Не стоит забывать о том, что показатель изменяется, он не остается постоянным. Изменения пропорционально растяжению.
3. Изначальное растяжение обозначается буквой l, для определения первоначального значение силу упругости применяется формула F=kl. В данной формуле используется коэффициент k, который обозначает жесткость.

Приведенная выше информация указывает на то, что провести расчет требуемого показателя проводится следующим образом: E=kl 2 /2. В этом случае величина во многом зависит от удлинения и коэффициента жесткости.

Контрольные вопросы

Что называется деформацией? Какие деформации называются упругими? Приведите примеры упругих деформаций.

Какова физическая сущность упругих сил?

Сформулируйте закон Гука? Когда он справедлив?

Дайте объяснение качественной диаграмме напряжений. Что такое предел пропорциональности, упругости и прочности?

Что такое упругий гистерезис и упругое последействие?

Каков физический смысл модуля Юнга и модуля сдвига?

Что такое упругое последействие?

Выведите выражения для деформаций при всестороннем растяжении.

Что называется коэффициентом Пуассона?

Определите энергию деформированного тела.

Что называется плотностью упругой энергии? Получите формулы этой энергии при растяжении и сдвиге.

А. mv²/2 Б.mv В.mgh Г. kx²/2 2. Каково наименование единицы кинетической энергии, выраженное через основные единицы Международной системы? А.1кг·м Б.1 кг·м/с В.1кг·м²/с Г.1кг·м²/с² 3. Чему равна кинетическая энергия тела массой 3 кг, движущегося со скоростью 4 м/с?

Читать также: Почему стиральная машинка сильно вибрирует при отжиме

А. 6 Дж. Б. 12 Дж. В.24Дж. Г.48Дж.

4. Как изменится потенциальная энергия упруго деформированного тела при увеличении его деформации в три раза?

À. Не изменится. Б. Увеличится в 3 раза. . Увеличится в 9 раз. Г. Увеличится в 27 раз.

Два автомобиля с одинаковыми массами m движутся со скоростями v и 3v относительно Земли в одном направлении. Чему равна кинетическая энергия второго автомобиля в системе отсчета, связанной с первым автомобилем?

А.mv² Б.2mv² В.3mv² Г.4mv² 6.Каково наименование единицы работы, выраженное через основные единицы Международной системы? А.1кг Б.1кг·м/с В.1кг·м/с² Г.1кг·м²/с² 7.По какой формуле следует рассчитывать работу си­лы F, если между направлением силы и перемещения S угол a ? А.(F/S)·cosα Б.F·S·sinα В.F·S·cosα Г.(F·S)·sinα

9. Тело массой 1 кг силой 30 Н поднимается на высо­ту 5 м. Чему равна работа этой силы?

А .0 Дж. Б. 50 Дж. В. 100 Дж. Г. 150 Дж.

Кинетическая энергия тела в момент бросания равна 200 Дж. Определите, до какой высоты от поверхности земли может подняться тело, если его масса равна 500 г.

Башенный кран поднимает бетонную плиту массой 2 т на высоту 15 м. Чему равна работа силы тяжести, действующей на плиту?

11-б. Нитяной и пружинный маятники

§ 11-б. Нитяной и пружинный маятники

Познакомимся с физической моделью нитяной маятник.

Взгляните на рисунок. Вы видите кирпич, подвешенный на широкой ленте, и тяжёлый шарик, подвешенный на нити. Толкнём их рукой, и оба тела начнут совершать колебания – станутмаятниками. Изучить колебания – значит найти способы описания колебаний и выявить их закономерности. Удобен ли для этого кирпичный маятник? Конечно, нет.

Во-первых, потому, что он большой, и при его качаниях будет велика сила сопротивления воздуха.

Во-вторых, лента подвешена за два конца, и при качаниях её половины будут натягиваться неодинаково, из-за чего кирпич будет двигаться зигзагами. Тяжёлый шарик на нити более удобен для изучения колебаний.

Нитяным маятником

называют тело на невесомой нерастяжимой нити, совершающее колебания

Для этой модели важно, чтобы размеры тела были малы по сравнению с длиной нити

В таком случае говорят: формой и размерами тела можно пренебречь (то есть в данных условиях не принимать их во внимание). Опыты показывают: если на тело нитяного маятника действуют только сила тяжести и сила упругости, он совершает колебания с постоянным периодом

При этом, если амплитуда колебаний невелика по сравнению с длиной нити (говорят: маятник совершает малые колебания), то период колебаний нитяного маятника можно подсчитать по формуле, которая помещена в рамке.

Вы видите, что период малых колебаний нитяного маятника не зависит от его массы, а определяется лишь длиной нити l и коэффициентом g.

Например, при увеличении длины нити в 4 раза, период колебаний маятника возрастёт в 2 раза (что равно √4 раз).

Рассмотрим вторую модель: пружинный маятник

– тело на пружине, совершающее колебания

При этом важно, чтобы один конец пружины был закреплён, а её масса была мала по сравнению с массой тела (то есть массой пружины можно было бы пренебречь). Опыты показывают: если на тело пружинного маятника действуют только сила тяжести и сила упругости, он совершает колебания с постоянным периодом

При этом, если амплитуда колебаний невелика по сравнению с длиной пружины (то есть она деформируется упруго), то период колебаний пружинного маятника можно подсчитать по формуле, которая помещена в рамке.

Итак, период малых колебаний пружинного маятника не зависит от коэффициента силы тяжести, а определяется лишь массой тела m и коэффициентом k, характеризующим жёсткость пружины.

Например, при увеличении массы груза в 9 раз, период колебаний маятника возрастёт в 3 раза (что равно √9 раз).

Наряду со свободными колебаниями,

когда маятник выведен из положения равновесия и предоставлен самому себе, существуют такжевынужденные колебания иавтоколебания. Обратимся к рисунку.

Под гирей, висящей на пружине, расположен электромагнит.

Если мы будем попеременно включать и выключать ток, то гиря начнёт совершать вынужденные колебания,

частота которых зависит от частоты внешнего воздействия.

Однако маятник может сам регулировать поступление энергии, совершая автоколебания.

Взгляните: средний провод зажат прищепкой и касается гири, пока она вверху.

Ток, проходя через пружину, гирю, средний провод и электромагнит, намагничивает его сердечник. Притягиваясь, гиря движется вниз. Вскоре она отсоединяется от среднего провода, ток прекращается, и магнитное поле исчезает.

Под действием пружины гиря поднимается вверх и снова замыкает цепь.

Колебательные и волновые явленияФормулы Физика Теория 8 класс

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.

стоимость заказа

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!