Что такое скорость вращения шпинделя и подача?
Скорость вращения — один из основных параметров шпинделя. Он выражается в оборотах в минуту (об/мин) или герцах (Гц). В портальных станках с ЧПУ не используется сложных по конструкции механических коробок передач и скорость регулируется электронными компонентами. С увеличением скорости вращения растет производительность станка и снижается ресурс режущего инструмента. Последнее связано с выделением избыточного количества тепла, которое не успевает рассеиваться. В результате перегрева падает твердость режущих кромок, и они теряют свою остроту.
Скорость подачи, или линейного перемещения, измеряется в миллиметрах в минуту (мм/мин) и влияет на объем снимаемого материала в единицу времени. На портальных станках без механизма вращения заготовки регулируются скорости перемещения портала, каретки и вертикального движения шпинделя. При составлении управляющих программ стараются задать максимально возможные подачи, при этом должно выполняться условие сохранения целостности фрезы. Избыточная скорость приводит к появлению сколов на режущих кромках поломка или деформация хвостовика.
Векторные величины, характеризующие вращательное движение тела
| Угловая скорость и угловое ускорение тела являются векторными величинами. Эти векторы направлены вдоль оси вращения (аксиальные векторы), а их длина определяет величину соответствующих характеристик вращательного движения. Направление векторов определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения буравчика, рукоятка которого движется в том же направлении, что и тело. |
Определение:Если тело участвует одновременно в нескольких вращательных движениях, то результирующая угловая скорость определяется по правилу векторного (геометрического) сложения:
Величина результирующей угловой скорости определяется по аналогии с формулой (Сложение движений):
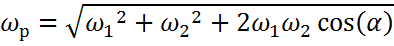
или, если оси вращения перпендикулярны друг другу
Примечание: Результирующее угловое ускорение определяется аналогичным образом. Графически результирующую можно найти как диагональ параллелограмма скоростей или ускорений.
Расчет скорости вращения шпинделя токарного или фрезерного станка
Зачастую происходит так, что по паспорту известно номинальное количество оборотов, но непонятно, насколько быстро лезвие оборудования проходит свой путь по заготовке. В таких случаях нужно лишь воспользоваться обратным соотношением:
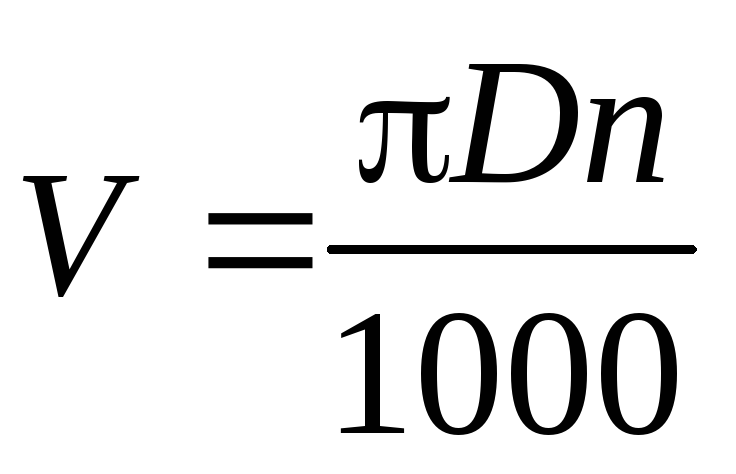
Отсюда ясно, что два этих параметра взаимосвязаны, и один выражает собой другой, а значит влияет на:
- Производительность труда – повышается, если деталь получается слишком дорогой в изготовлении; однако существенно увеличить его на практике можно далеко не всегда, даже если возможности спецтехники позволяют это сделать; вы помните – эксплуатация инструмента в слишком жестком режиме приводит к его перегреву и преждевременному износу.
- Итоговую степень шероховатости поверхности – чем быстрее движется вал, тем более гладкой становится плоскость, но и тем сильнее нагрузка на лезвие, поэтому высокие обороты на практике используются не постоянно, а лишь при проведении отдельных операций, чаще всего чистовой обработки.
Вращательное движение тела, формулы
При вращательном движении твердого тела все элементы его массы, не лежащие на оси вращения, совершают движение по окружности. Аналогично и материальная точка, находящаяся на расстоянии r > 0 от оси вращения, также совершает движение по окружности, как и любое тело, достаточно удаленное от оси вращения. Линейное перемещение Sл, линейная скорость uл и линейное ускорение aл при таком движении связаны между собой обычными для поступательного движения соотношениями. |
Кроме того, эти величины связаны определенным образом с угловым перемещением ?, угловой скоростью ? и угловым ускорением ?.
| Sл | перемещение тела по траектории, | метр |
|---|---|---|
| Uл | скорость тела при движении по траектории, | метр / секунда |
| aл | ускорение данного тела при движении по траектории, | метр / секунда2 |
| r | радиус траектории, | метр |
| d | диаметр траектории, | метр |
| ? | угловое перемещение тела, | радиан |
| ? | угловая скорость тела, | радиан / секунда |
| ? | угловое ускорение тела, | радиан / секунда2 |
| f | частота, | Герц |
Примечание:Формулы справедливы для постоянных, мгновенных и средних величин, во всех случаях движения тела по окружности.
Распространенные ошибки при выборе режимов резания
Очень часто начинающие токари и фрезеровщики не согласовывают скорости – это оборачивается концентрацией напряжений на кромке, а значит повышает вероятность поломки инструмента в таких «критических» точках и вызывает другие проблемы.
Есть две классические ситуации:
- Максимальные обороты при медленной подаче – при этом серьезно падает качество обработки. Кроме того, резец будет не снимать стружку, а лишь давить на поверхность, сначала лишь шлифуя ее, а потом уже вызывая прижог; при этом не просто действуя вхолостую, а даже теряя в прочности, ведь будет наблюдаться отгибание кромки.
- Обратная ситуация приводит к тому, что лезвие убирает слишком много материала и вместе с тем испытывает чрезмерную нагрузку, в результате чего скалывается и оставляет царапины и другие дефекты на той плоскости, которая должна быть гладкой.
Поэтому на практике нужно проводить расчет частоты вращения шпинделя для каждой технологической операции и, на основе полученных результатов, соотносить подачу, чтобы обеспечивать не только скорость, но и точность, и безопасность процесса. Тем более что все величины можно принимать в некотором диапазоне – всегда есть место для допусков. Помните, что длительная эксплуатация инструмента – следствие правильного подхода, тогда как неожиданная поломка – результат допущенных ошибок.
И универсальный совет – проводите обработку в несколько этапов: сначала черновую, по максимуму снимая ненужный металл, потом чистовую, более медленно, и, наконец, финишную – для шлифовки мельчайших неровностей.
Расчет модуля зубчатых передач
Расчёт модуля цилиндрических передач по допускаемым контактным напряжениям и напряжениям изгиба
Расчетный модуль по контактным напряжениям
Расчетный модуль по напряжениям изгиба
где Сk = 3530,9 и Си = 84,87 — коэффициенты, зависящие от материала зубчатой пары, для стальной шестерни и стального колеса
U — передаточное число зубчатой пары;
— коэффициент ширины колеса;
— число зубьев шестерни;
=310 МПа и — допускаемые контактные напряжения и напряжения изгиба,
N — номинальная передаваемая мощность, кВт, определяется по формуле:
где Nэ = 8 кВт — мощность электродвигателя, — КПД кинематической цепи от двигателя до рассчитываемой шестерни
Y — коэффициент формы зуба, зависит от числа зубьев;
и — коэффициенты долговечности колес, рассчитываются по формулам:
станок привод муфта подшипник
где и -коэффициенты, учитывающие изменение мощности.
и — коэффициенты, учитывающие переменность частот вращения шестерни;
— долговечность зубчатой пары, ч
— минимальная частота вращения в группе, мин-1
— скоростной коэффициент, определяется по формуле
Где: C — коэффициент, зависящий от материала и точности обработки шестерен; для закаленных С = 9
V- допускаемая окружная линейная скорость в зубчатой передаче; для закаленных V = 9
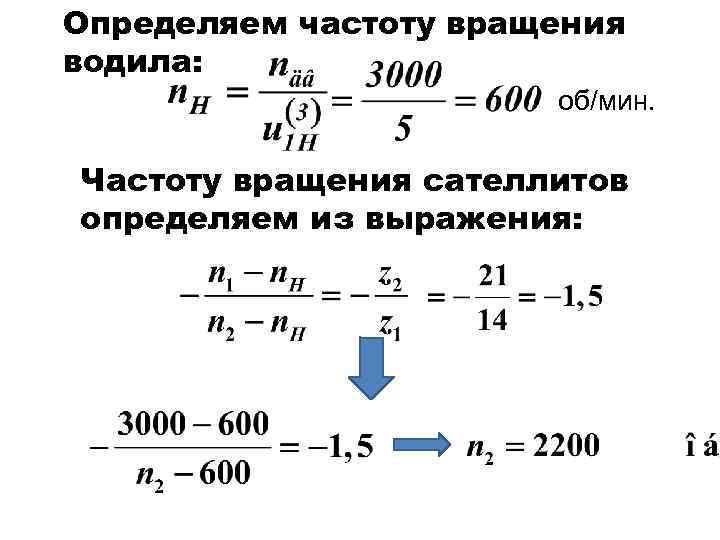
об/мин. — частота вращения шестерни
об/мин. — минимальная частота в группе
— число зубьев шестерни
Y=0,108 — коэффициент формы зуба
Стандартное значение модуля по ГОСТ 9563 — 60: 5
об/мин. — частота вращения шестерни
об/мин. — минимальная частота в группе
— число зубьев шестерни
Y=0,107 — коэффициент формы зуба
Стандартное значение модуля по ГОСТ 9563 — 60: 5
об/мин. — частота вращения шестерни
об/мин. — минимальная частота в группе
— число зубьев шестерни
Y=0,04 — коэффициент формы зуба
Стандартное значение модуля по ГОСТ 9563 — 60: 6
об/мин. — частота вращения шестерни
об/мин. — минимальная частота в группе
— число зубьев шестерни
Y=0,134 — коэффициент формы зуба
Стандартное значение модуля по ГОСТ 9563 — 60: 6
Определяем модули зубчатых зацеплений с помощью ЭВМ по программе кафедры ОАМ ModLZubCos и сводим все рассчитанные значения в таблицу
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Циклическая частота вращения (обращения)
Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.
Циклическая частота вращения – это количество оборотов тела за 2*π секунды.
У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.
Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.
При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:
Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Что такое шпиндель
Шпиндель — единая ось в жестком диске, на которой установлено несколько магнитных пластин. Эти пластины закреплены на шпинделе на строго определенном расстоянии. Расстояние должно быть таким, чтобы при вращении пластин считывающие головки могли читать и записывать на диск, но при этом не касались поверхности пластин.
Чтобы диск нормально функционировал, двигатель шпинделя должен обеспечивать стабильное вращение магнитных пластин на протяжении тысяч часов. Поэтому неудивительно, что иногда проблемы с диском связаны именно с заклиниванием шпинделя, а вовсе не с ошибками в файловой системе.
Двигатель отвечает за вращение пластин, и это позволяет работать жесткому диску.
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
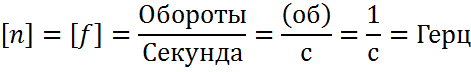
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если n — число оборотов, f — частота, T — продолжительность одного оборота, период, ? — угловое перемещение, N — полное число оборотов, t — время, продолжительность вращения, ? — угловая частота,
то
Угловое перемещение равно произведению полного числа оборотов на 2?:
Угловая скорость
Из формулы для одного оборота следует:
Обратите внимание:• формулы справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.• вопреки своему названию число оборотов n — это не число, а физическая величина.• следует различать число оборотов n и полное число оборотов N
Скорость вращения шпинделя
При рассмотрении формулы, которая применяется для расчетов частоты вращения шпинделя, уделяется внимание скорости. Она также должна выбираться в зависимости от определенных условий эксплуатации оборудования
Для расчета скорости вращения -шпинделя станка может применяться формула: v=пdn/1000.
Скорость вращения токарного станка по металлу используется в качестве показателя скорости резания. От него зависит следующее:
- Производительность труда. Стоимость изделия во многом зависит от того, сколько времени было потрачено на его получение. Для повышений производительности труда следует существенно повысить значение скорости резания. Однако это не всегда можно провести, так как слишком высокий показатель может привести к серьезным проблемам, к примеру, нагреву инструмента или износу основной части.
- Шероховатость получаемой поверхности также варьирует в большом диапазоне. С увеличением скорости резания можно существенно повысить качество готового изделия. Поэтому высокие значения применяются в большинстве случаев при чистовом точении.
Выбор определенного показателя скорости вращения шпинделя проводится в зависимости от возможностей применяемого оборудования. Слишком высокий показатель нельзя устанавливать по причине того, что подобная эксплуатация оборудования приводит к сильному износу.
В заключение отметим, что неправильный расчет частоты вращения может привести к весьма тяжелым последствиям. Это связано с возможностью износа привода, а также других элементов. Не рекомендуется выбирать максимальные показателе частоты вращения и скорости резания, так как это может привести к повышенному износу и возможности износа применяемого инструмента.
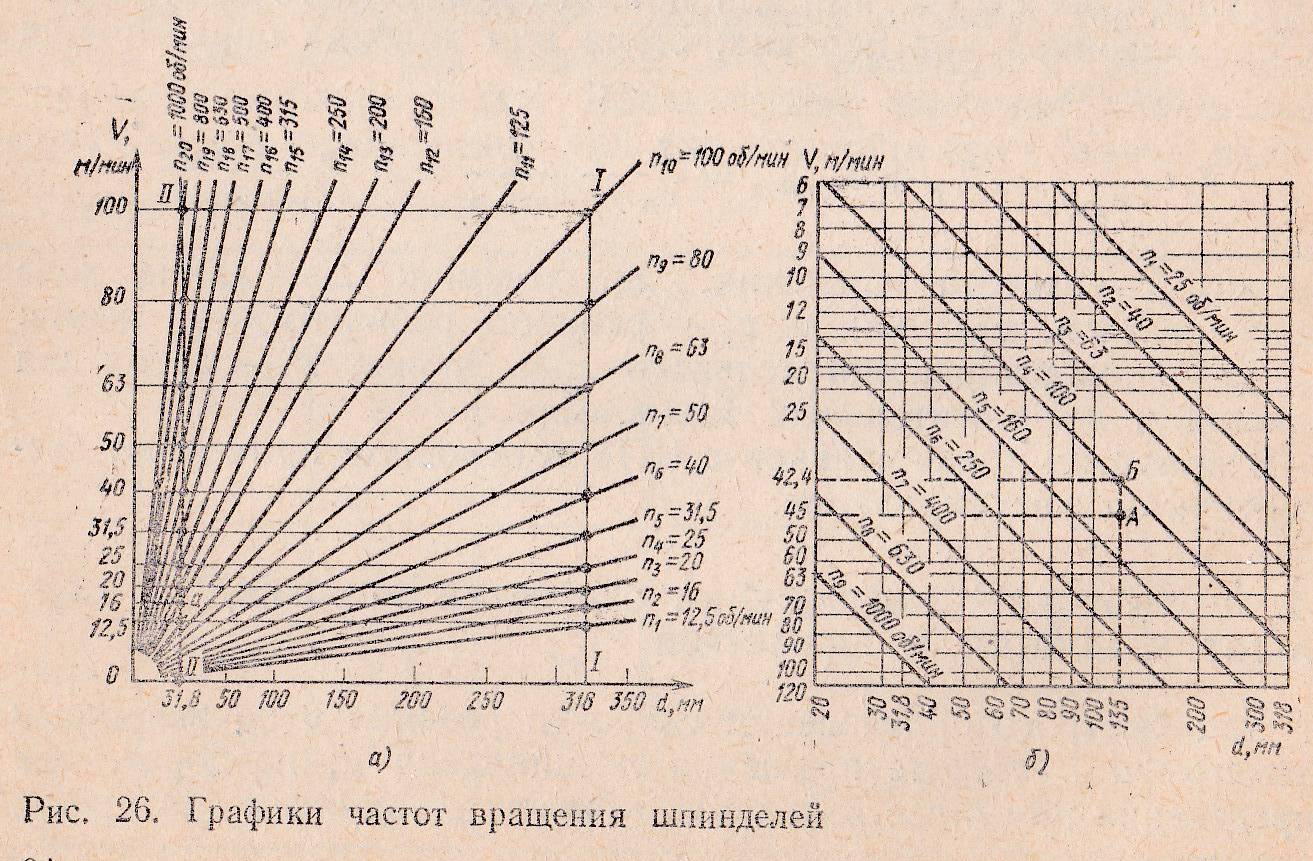
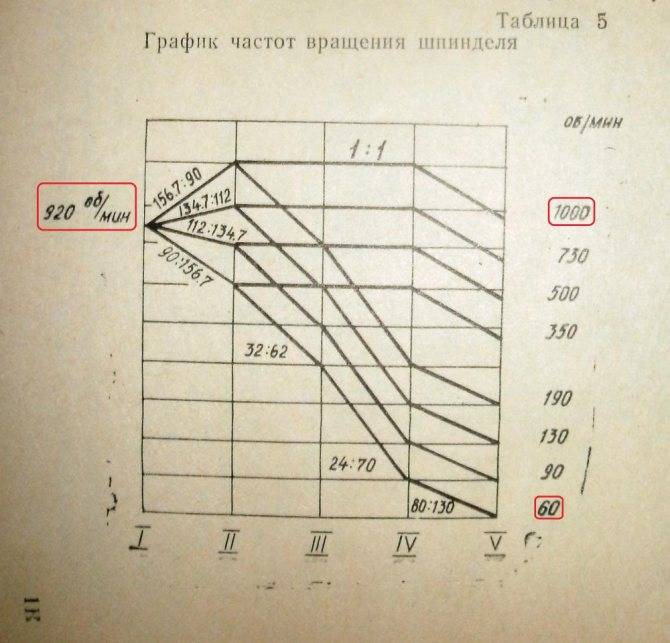
График – частота – вращение
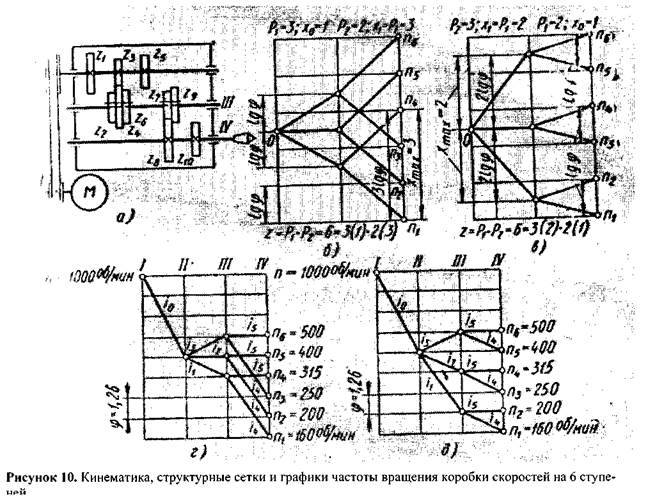
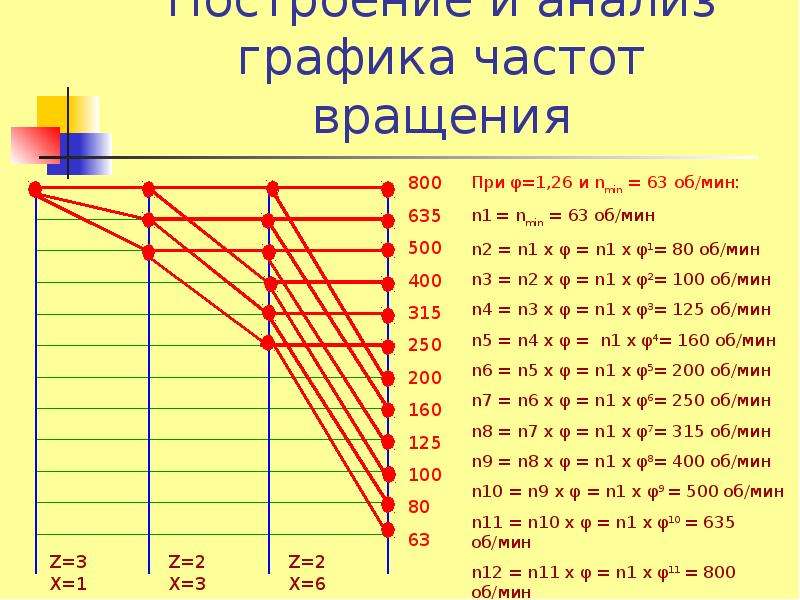
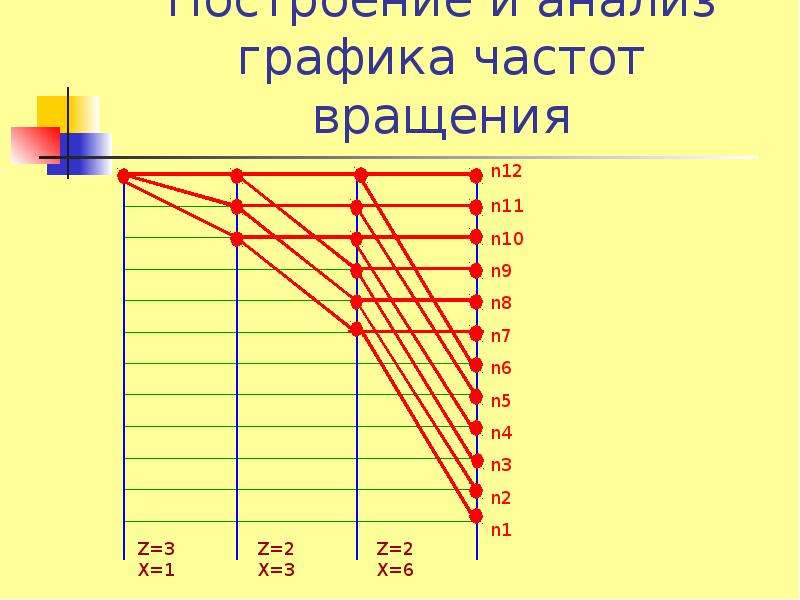
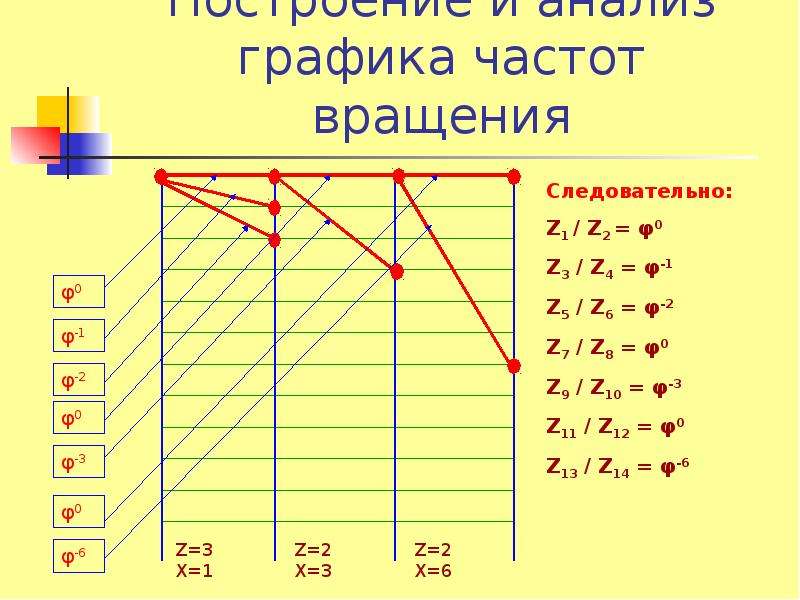
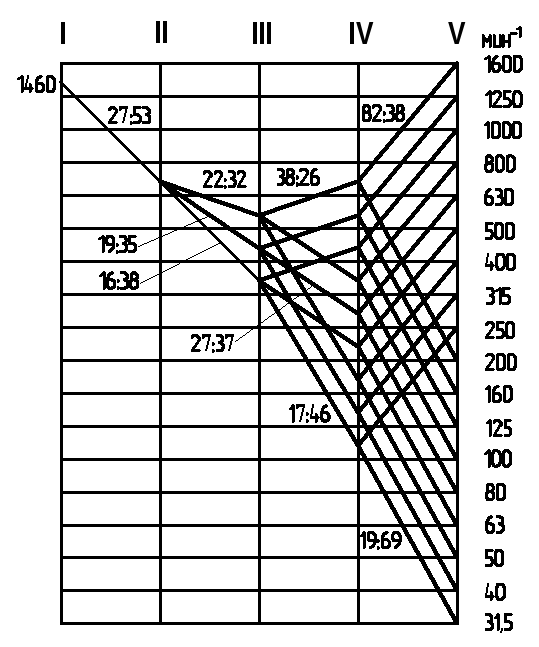
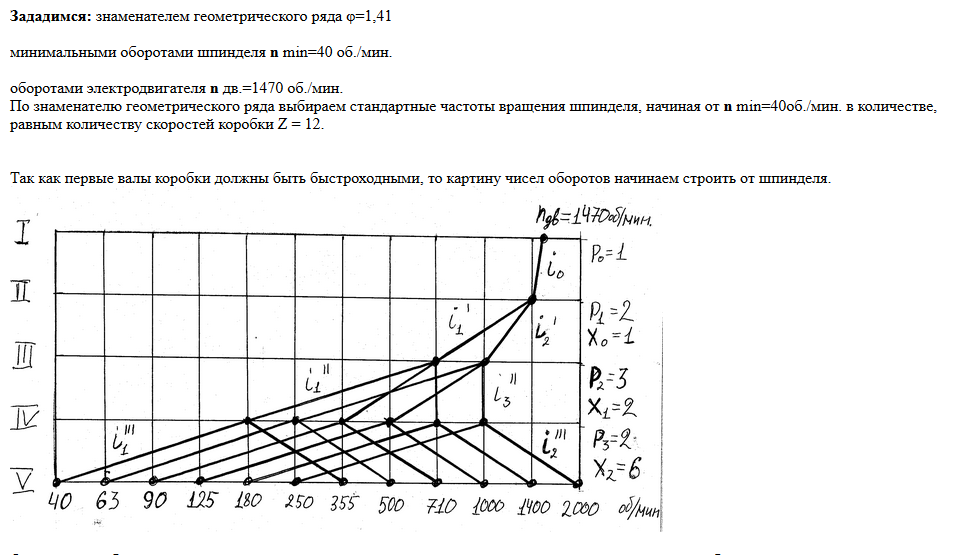
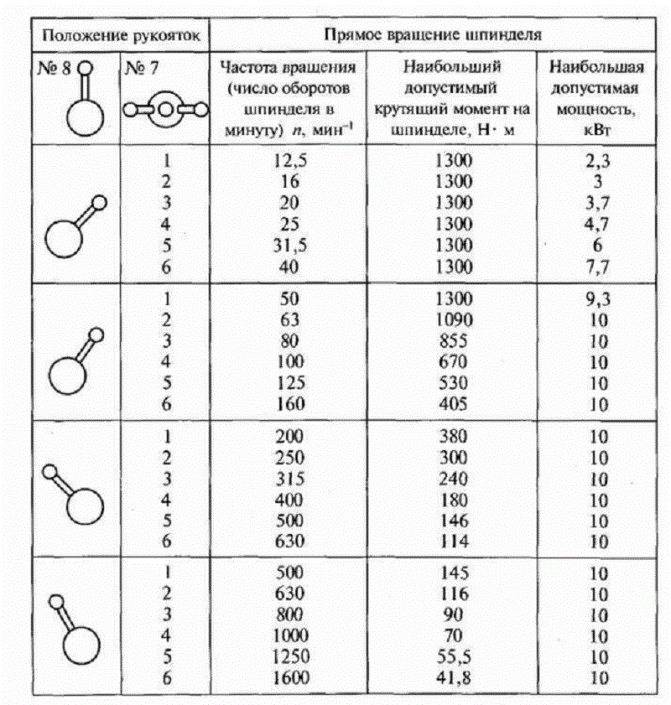
Получение требуемого геометрического ряда частот вращения шпинделя может быть осуществлено несколькими вариантами графиков частот вращения с различными передаточными отношениями промежуточных пар зубчатых колес. Перед построением графика частот вращения скачала строят структурные сетки.
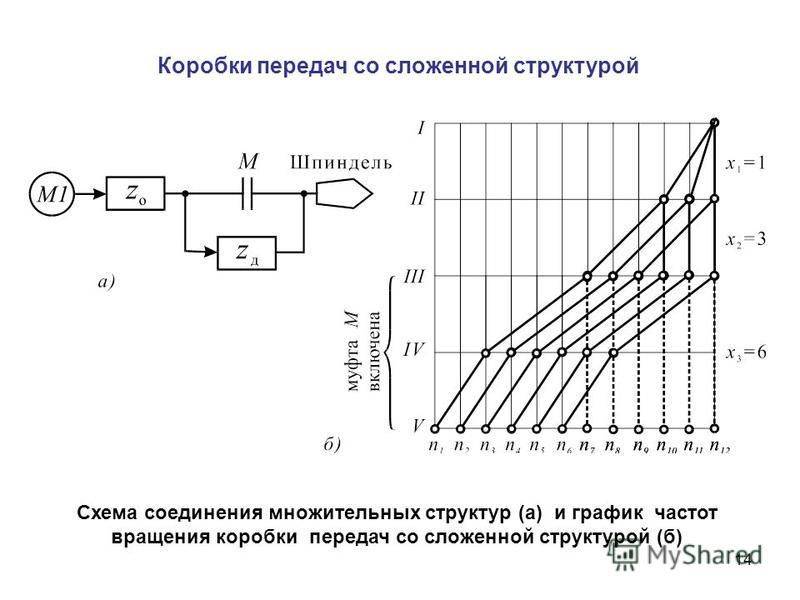
На основе принятого варианта структурной сетки возможны различные варианты графика частот вращений ( см. рис. 48) в зависимости от дополнительных одиночных передач и выбранных окончательно передаточных отношений. При построении графика частот вращений обычно достаточно быстроходный электродвигатель на 1500 или 3000 об / мин необходимо использовать для получения более низких частот вращений шпинделя. Осуществление общей редукции при этом желательно проводить таким образом, чтобы промежуточные валы сохраняли быстроходность.
Получение требуемого геометрического ряда частот вращения шпинделя может быть осуществлено несколькими вариантами графиков частот вращения с различными передаточными отношениями промежуточных пар зубчатых колес. Перед построением графика частот вращения скачала строят структурные сетки.
Однако, как правило, используют только графоаналитический метод. При графоаналитическом методе последовательно строят структурную сетку и график частоты вращения.
| Варианты структурных сеток коробок передач для двенадцати ступеней частот вращения. |
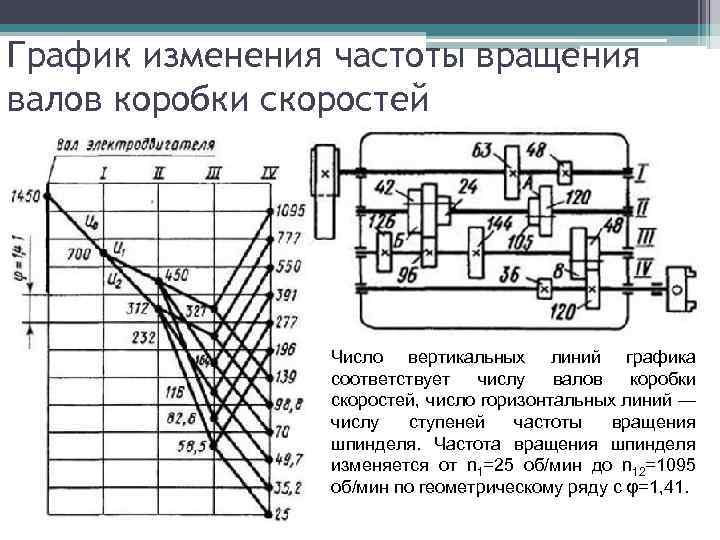
Структурная сетка позволяет определить количество ступеней частот вращения на валах; количество групповых передач и порядок их конструктивного расположения; число передач в каждой группе; диапазоны регулирования групповых передач, которые равны ср в степени, равной числу интервалов Igcp, заключенному между крайними лучами, выходящими из одной точки; диапазоны регулирования на промежуточных валах. Структурная сетка не дает фактических значений частот вращения и передаточных отношений передач в группах. Для определения этих параметров строят график частот вращения. Для его построения должны быть известны: а) знаменатель ряда ср.
Такое распределение характеристик передач обеспечивает минимальные крутящие моменты, так как соответствует более высоким частотам вращения первых групп передач из всех возможных вариантов. Структурная сетка позволяет определить передаточные отношения в группах и построить график частот вращения. Для понижающих коробок необходимо найти минимальные передаточные отношения.
Основными вопросами, которые необходимо решить при выборе электродвигателя для аппаратуры, являются выбор типа двигателя с электромеханическими свойствами, отвечающими характеру нагрузки, и определение номинальной мощности электродвигателя. Мощность электродвигателя выбирают, исходя из необходимости обеспечить выполнение заданной работы электропривода при соблюдений нормального теплового режима и допустимой механической перегрузки двигателя. При этом следует учитывать нагрузку привода не только в установившемся режиме работы, но и во время переход-ных режимов
Важное значение имеет также цикличность работы привода, которая характеризуется графиком частоты вращения при заданном графике статического момента приводимого механизма. По графику частоты вращения определяют ускорение для любого момента времени, затем момент инерции всех вращающихся частей механизма, приведенный к валу двигателя, и вычисляют значения динамических моментов
Алгебраическое сложение статических и динамических моментов нагрузки позволяет получить график полного момента, по которому и рассчитывают мощность двигателя.
Что такое скорость и частота вращения шпинделя
Начнем с определений. В случае с подачей это динамика линейного перемещения – вала, каретки, портала – за единицу времени. Оказывает прямое влияние на объем снятия материала, поэтому ее стараются максимизировать, но так, чтобы целостность резца не подвергалась риску. Если задать избыточное значение характеристики, такое, какое инструмент не сможет выдержать на практике, это обернется сколами на лезвии или деформацией хвостовика. Также нужно учитывать чрезмерный нагрев: в погоне за производительностью не стоит жертвовать остротой и ресурсом кромок.
В свою очередь, частота вращения шпинделя – это то количество оборотов, которое он совершает за определенный срок. Чем она выше, тем большее количество деталей можно обработать за единицу времени, но и тем быстрее резец выходит из строя. Почему? Потому что выделяемое в процессе гравировки или расточки тепло просто не рассеивается до конца и негативно влияет на все элементы системы в принципе. На практике величина данного параметра автоматически регулируется встроенной электроникой – в портальном оборудовании, в том числе и с ЧПУ, в составе которого нет конструкционно сложных механических узлов (например, коробок передач).

Типы шпинделей по числу оборотов
По данному показателю все валы разделяют на 3 категории:
- Маломощные – до 0,8 кВт включительно – устанавливаются на негабаритной технике, использующейся в небольших частных мастерских для решения упрощенных бытовых задач; развивают от 3 до 9 тысяч об/мин.
- Средние – от 1,5 до 5 кВт – применимы в стандартных условиях, для обработки заготовок из дерева, пластика, мягких металлов, а также для нанесения гравировки; поддерживают от 12 до 18 тысяч об/мин.
- Высокопроизводительные – от 5 кВт и выше – предназначены для промышленного оборудования, призванного решать самые масштабные и серьезные задачи; в общем случае доходят до 24 тысяч об/мин, хотя данный показатель не всегда является безусловным плюсом – те же твердосплавные или тонкие фрезы на такой скорости изнашиваются очень быстро.
Угловая частота, период и угловая скорость
Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:
T = 2*pi/ω
Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:
f = 2*pi/T
Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.
Сравнивая две последние формулы, приходим к следующему равенству:
f = ω
Это равенство означает следующее:
- формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
- так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.
Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.
Угол поворота и период обращения
Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.
Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать 1/2, 1/4 оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.
Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки
Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.
В этом случае находят применения такие характеристики, как:
Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.