Шкала измерений

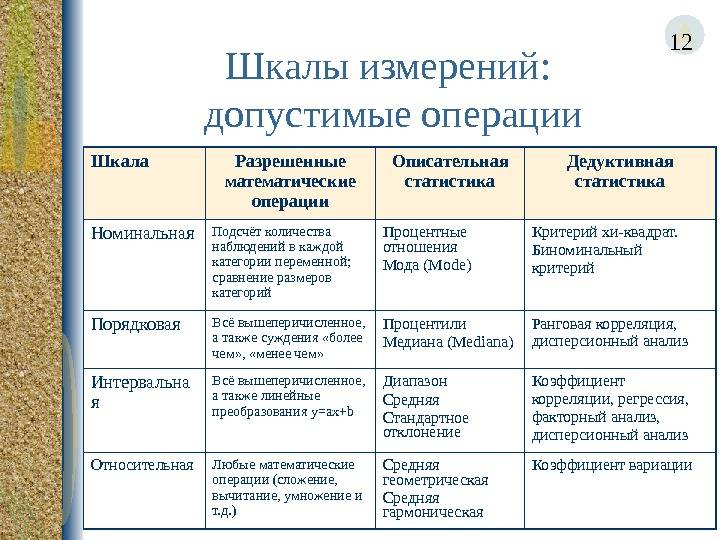
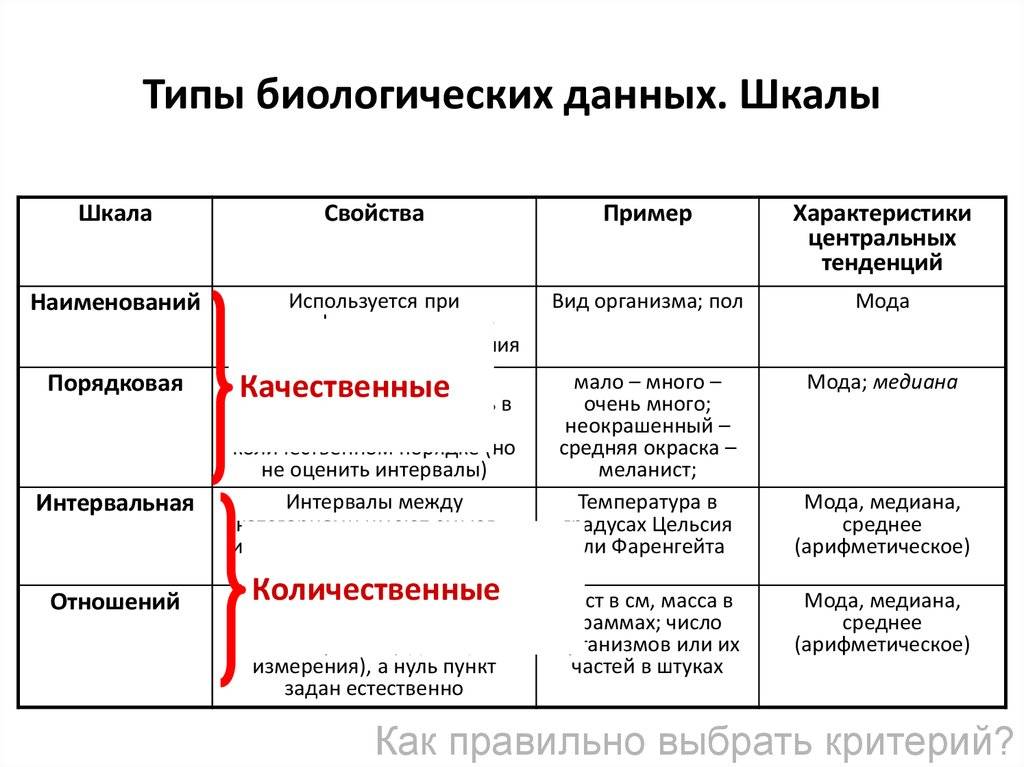
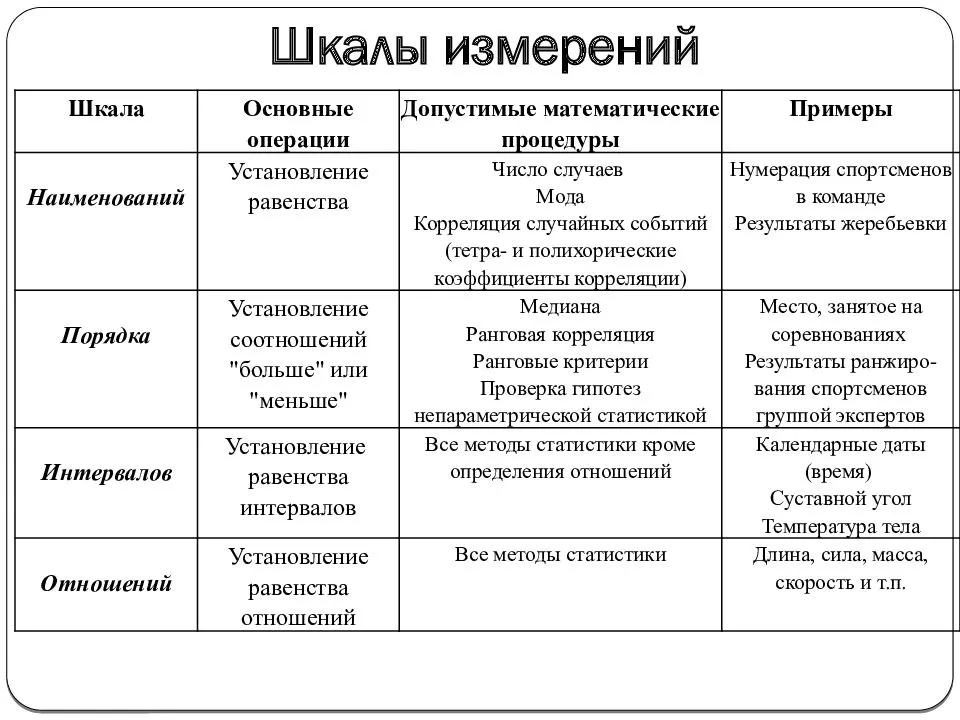
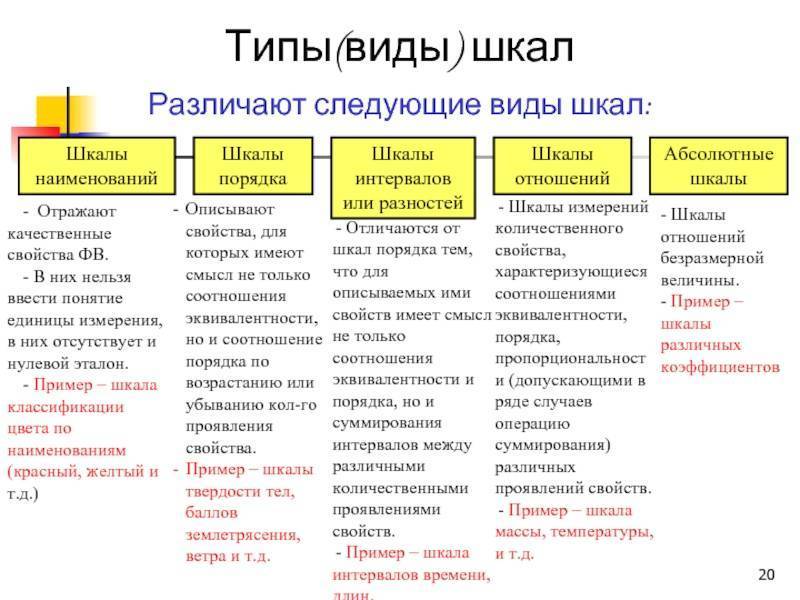
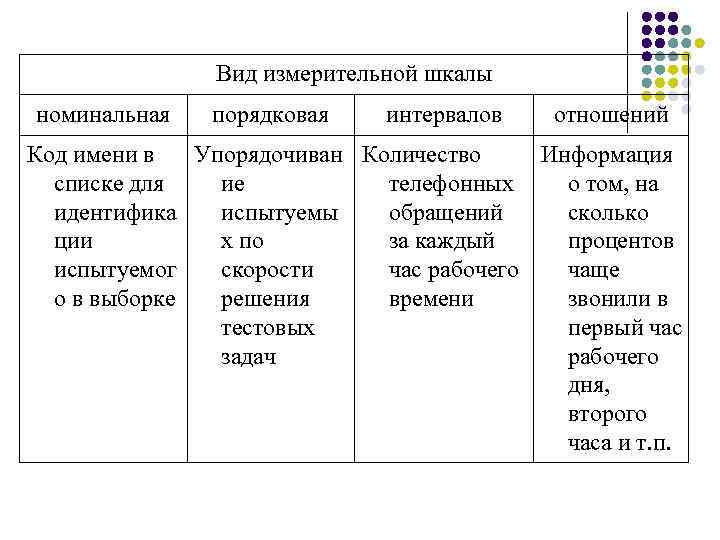
2.2. Условия упорядоченности

Номера так же, как и числа, упорядочены; первые — произвольные образом, вторые — на основании двух отношений, существующих между упорядоченными объектами, — отношений, специальное название которых транзитивность и антисимметричность.

Транзитивность — если А находится в некотором отношении к В, а В к С, то А находится в том же отношении к С.

Симметричность — если А находится в некотором отношения к В, то В находится в том же отношении к А.

Антисимметричность — если А больше В, то В меньше А.

Отношение порядка применимо к свойству твердости: все тела, к которым применимо это понятие, связаны между собой транзитивным и антисимметричным отношением „тверже, чем» или обратным отношением „мягче, чем»; каждое тело, твердость„которого мы хотим определить, либо тверже любого другого тела того же класса, либо мягче него.

Отношение „тверже, чем» является транзитивным и антисимметричным.

Оно транзитивно потому, что если Аоставляет царапину на В, а В — на С, то Аоставляет царапину на С.

Оно антисимметрично потому, что если Аоставляет царапину на В, то Вне оставляет царапину на А.

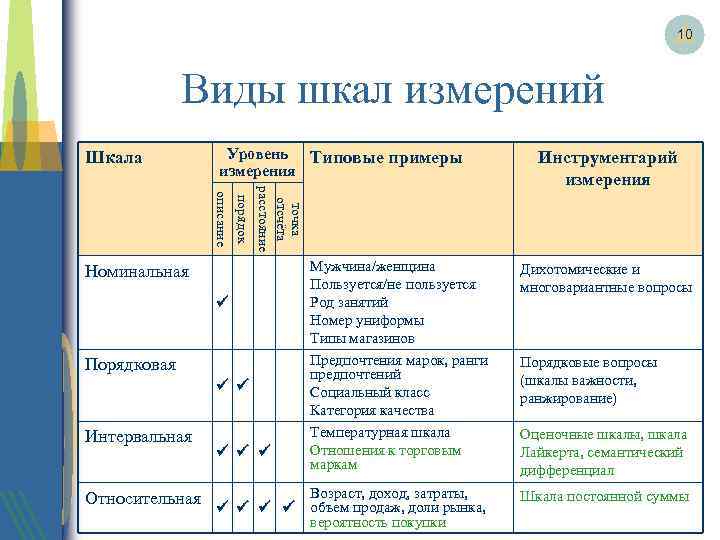
Типы шкал

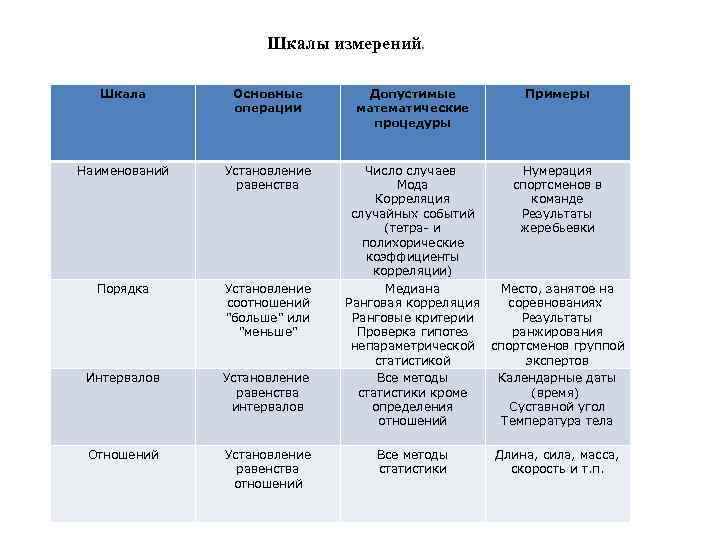
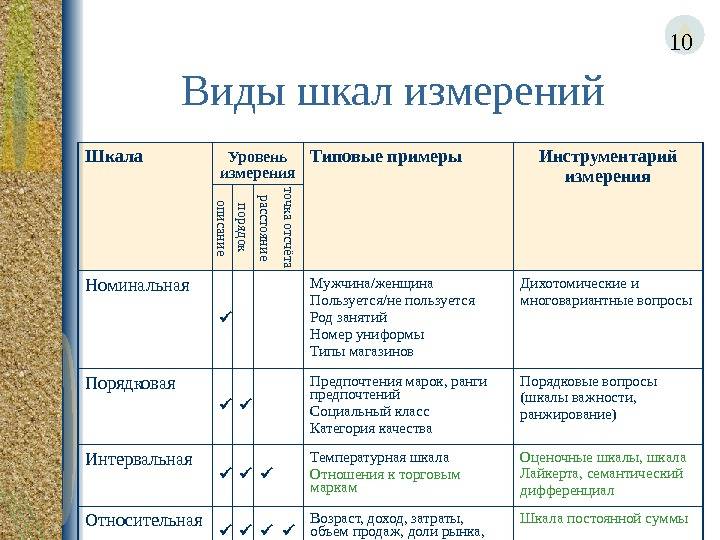
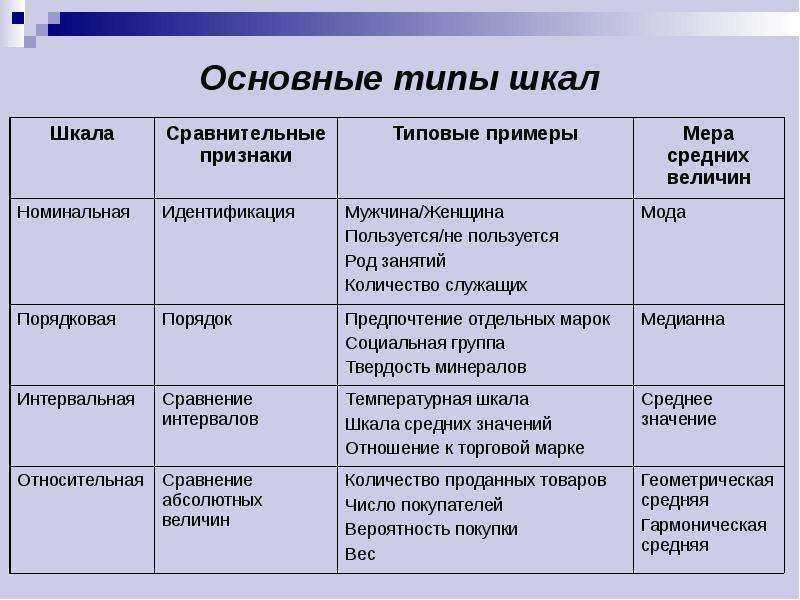
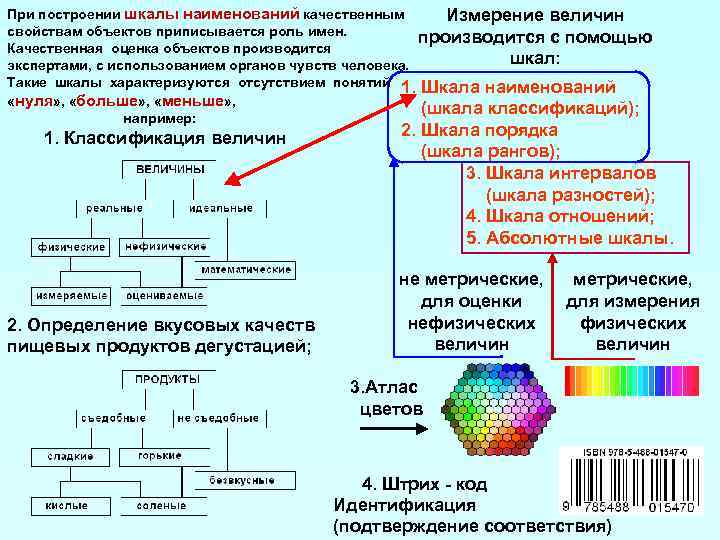
На сегодняшний день различают четыре основных типа шкал измерений: номинальная, порядковая, интервальная и относительная. Каждый тип шкалы обладает определенными признаками, которые рассматриваются ниже; сейчас же рассмотрим какую роль играет техника измерений в процессе классификации.

Часто при классификации исследователь не имеет возможности численно измерить исследуемый параметр. Например, отношение человека к чему-либо, степень его предпочтения и т.д. Способы измерения в данном случае отличаются от традиционных способов. Измерением в данном случае будет считаться любой способ приписывания числовых значений символам, которые отражают качественные характеристики объектов. При этом должны существовать устойчивые взаимосвязи между символами и качествами, которые они отражают. Иными словами, для осуществления кластеризации объекта с качественными характеристиками необходимо использовать приемы техники шкалирования.

В процессе использования техники шкал традиционно выделяют ряд стадий, качество выполнения которых оказывает непосредственное влияние на результат выделения кластеров. На первом этапе необходимо дать четкое определение тому, что собираются измерять. Далее следует указать, как измерение будет осуществлено на практике или что/кто конкретно подлежит измерению. После чего выбирают тип шкалы измерения, который предопределяет метод сбора информации. Любые измерения связаны с ошибками, но поскольку измерение в данном случае имеет специфику, то исследователь может самостоятельно оценить некоторые случайные отклонения исследуемого параметра и исключить его из кластера. Традиционно объекты наблюдения могут быть представлены в следующих типах шкал.

1 тип: номинальная или шкала наименований

Этот базовый и самый примитивный тип шкалы. При его использовании каждому объекту присваивается только идентификационный номер, как, например, номера игроков в спортивной команде, номера телефонов и т.д.

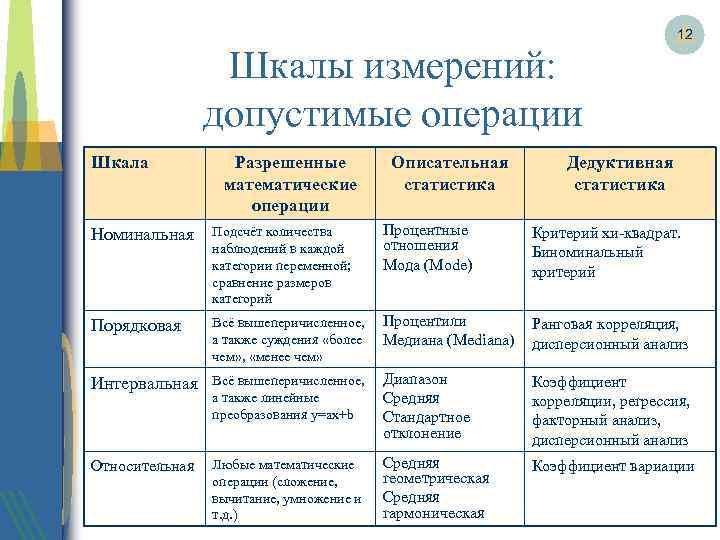
Операции в данной шкале:

2 тип: порядковая шкала

Этот тип шкалы определяет порядок или ранг объектов наблюдения. Расстояния между объектами, которые следуют друг за другом (по убыванию или по возрастанию) не являются равными. На основании результата ранжирования нельзя сказать, что расстояние между свойствами объектов и равны расстоянию между свойствами объектов и . Часто данный тип шкалы еще называют шкалой восприятия. Например, оценка качества вина по десятибалльной шкале – наиболее понравившееся качество 10 баллов, наименее – 1 балл.

Операции в данной шкале:

3 тип: интервальная шкала

В отличие от порядковой шкалы, здесь имеет значение не только порядок следования величин, но и величина интервала между ними. Пример для данного типа шкалы: температура воды в море утром – 18 градусов, вечером – 24, т.е. вечерняя на 5 градусов выше, но нельзя сказать, что она в 1.33 раз выше.

Операции, которые можно выполнять на базе этой шкалы:

4 тип: относительная или шкала отношений

В отличие от интервальной шкалы может отражать то, во сколько один показатель больше другого. Относительная шкала имеет нулевую точку, которая характеризует отсутствие измеряемого качества. Например: цена на товар. Здесь за точку отсчета можно взять «ноль» рублей. Отметим, что на практике не часто удается привести измерения к данному типу шкалы.

Операции для данной шкалы:

Медиана, мода, среднее, разброс

Рассмотрим пример: исследование охватило 200 человек с ожирением. Вес участников исследования колебался от 105 до 203 кг. Это разброс значений, или дисперсия. Средний вес составил 120 кг — это среднее значение веса в выборке. К примеру, 30 из 200 человек имели вес 115 кг. Остальные весили по‑разному, поэтому 115 — оказалось самым «популярным» значением веса в выборке, то есть модой ­веса.

Даже на базе этих данных мы можем составить представление о том, как выражен изучаемый признак: большинство участников исследования весило ближе к 100 кг, и только немногие весили около 200. Кроме определения «чистого» веса можно, например, ранжировать (разделить) пациентов по индексу массы тела — ИМТ. Например, 1 — ожирение первой степени (ИМТ 30–35), 2 — ожирение второй степени (ИМТ 35–40), 3 — ожирение третьей степени (ИМТ более 40). И тут мы плавно подходим к понятию шкал ­переменных.

Статистические шкалы

Введение

Грамотное применение статистических методов обработки данных во многом зависит от четкого понимания исследователем того, в какой статистической шкале они представлены. Непонимание этого может привести к тому, что исследователь получит результаты, которые не отражают действительное положение вещей и сделает неправильные выводы. Именно поэтому понимание того, в какой шкале представлены статистические данные является одним из необходимых условий успешной и грамотной статистической обработки.

Итак, приступим к тому, чтобы разобраться, что же такое статистические шкалы.

Определения и примеры

Шкала (от лат. «скале» — лестница) – элемент счетной системы, посредством которого происходит отнесение исследуемого объекта к определенной группе объектов.

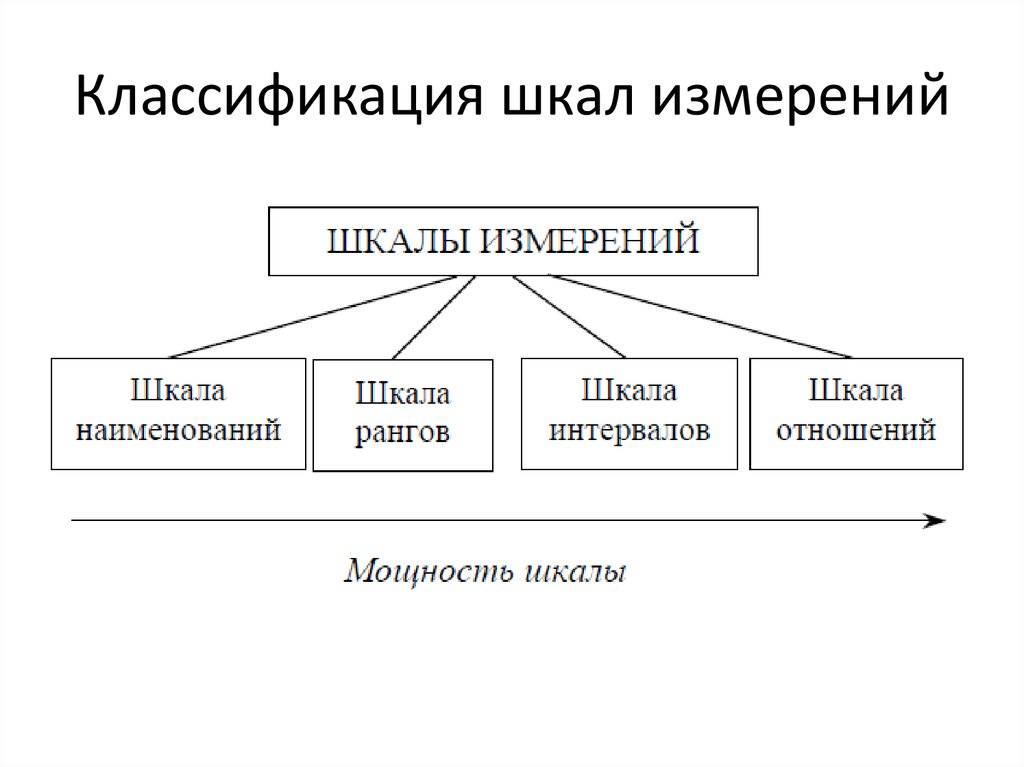
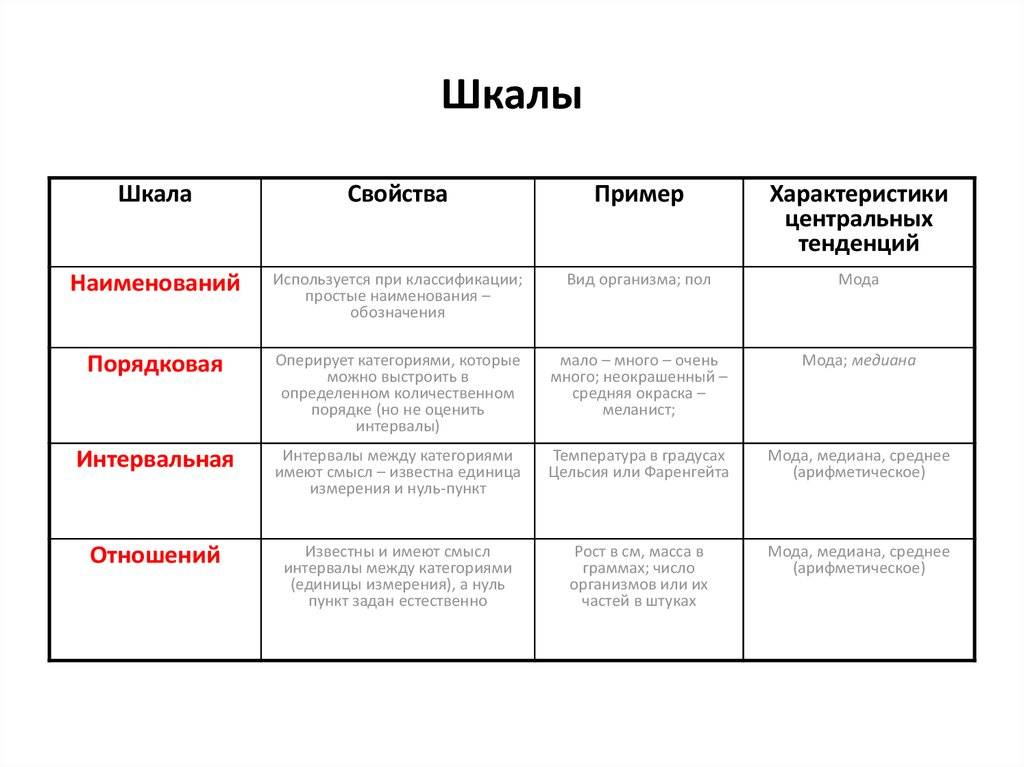
Статистические шкалы можно разделить на качественные и количественные. К качественным шкалам относится номинальная и порядковая шкалы. К количественным – интервальная шкала и шкала отношений.

Номинальная шкала – качественная шкала. Относится к самому элементарному типу измерения. В ней каждому оцениваемому объекту приписывается наименование или число.

Пример 1: Признак – пол. Цифрой «0» обозначаем женщин, цифрой «1» — мужчин. Очевидно, что расчет среднего арифметического не иимеет смысла.

Пример 2: Признак — Цвет волос: Цифрой «1» обозначаем брюнетов, цифрой «2» — шатенов, цифрой «3» –  блондинов, цифрой «4» – людей, имеющих рыжий цвет волос.

Пример 3: Номера на футболках спортсменов.

Более подробно о методах статистической обработки данных рассказано в книгах:

• Факторный анализ в педагогических исследованиях в области физической культуры и спорта
• Компьютерная обработка данных экспериментальных исследований
• Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта

Для области физической культуры и спорта использование номинальной шкалы очень важно, так как очень часто используется метод анкетного опроса. При этом результаты представлены в виде таблицы, в которой представлена абсолютная частота ответов на тот или иной вопрос (табл

1).

Таблица 1

Оценка мужчинами и женщинами своего психического состояния

Психическое состояние	Мужчины	Женщины	Всего
Крайне неустойчивое	3	16	19
Неустойчивое	22	18	40
Устойчивое	32	9	41
Очень устойчивое	5	1	6
Всего	62	44	100

Порядковая шкала (ранговая) – качественная шкала, использующая свойство чисел отражать отношение «больше – меньше».

В порядковой шкале нельзя сказать насколько или во сколько одно значение больше другого, но можно сказать какое больше, какое меньше. Очень часто статистические данные, представленные в порядковой шкале, измеряются в баллах.

Интервальная шкала – количественная шкала. В этой шкале устанавливается единица измерения.

В интервальной шкале, например, измеряется температура (по Цельсию или по Фаренгейту).

Шкала отношений. Для признаков, измеренных в шкале отношений можно дополнительно сказать: во сколько одно значение больше другого. Шкала отношений в отличие от интервальной шкалы обладает точкой нулевого отсчета.

Примерами статистических данных, представленных в шкале отношений являются признаки: рост, вес, температура по Кельвину.

Более подробное эта тема рассмотрена в литературе, ссылки на которую приведены ниже.

Литература

1. Барникова, И.Э. Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта: учеб. пособие / И.Э. Барникова; А.В. Самсонова; Национальный государственный университет физической культуры, спорта и здоровья им. П.Ф. Лесгафта, Санкт–Петербург. – СПб.: , 2017. – 103 с.
2. Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.

Замечания (описание)

Выбор шкал измерения не является проектным методом в общепринятом смысле» однако, не прибегая к измерениям, невозможно применять четкую методологию проектирования. Принципы измерения имеют следующее отношение к проектированию:

а) Важнейшие измерения при проектировании те, которые непосредственно связаны с задачами и критериями проекта

Поскольку задачи и критерии лишь редко можно измерить с помощью привычной пропорциональной шкалы, очень важно уметь пользоваться менее широко известными шкалами низшего порядка. В книгах Холла, Кофмана и Зигеля подробно рассматриваются такие шкалы

б) Для того чтобы понять некоторые из описанных в этой книге методов, требуется хотя бы элементарное знакомство с измерительными шкалами

Поэтому при обсуждении этих методов даются ссылки на манный раздел.

в) Инженеры, архитекторы и другие специалисты, для которых измерения имеют важное значение, как правило, не знают никаких измерительных шкал, кроме пропорциональных. В какой-то мере это объясняется тем, что задачи более высокого уровня, к которым применимы шкалы низшего порядка, традиционно решались на основании слыл и здравого смысла

В будущем их, однако, часто придется решать с помощью измерения и вычислений.

Зависимость вычислений от измерений и отношение точности к стоимости и величине штрафа редко освещаются в литературе, посвященной методам проектирования. Следует иметь в виду, что на тщательные размышления и действия, связанные с выполнением точных и полезных для практики измерений, требуется значительно больше времени и сил, чем для проектирования «сидя в кресле» Поэтому приведенный выше пример следует рассматривать лишь как беглый набросок тех размышлений, которые необходимы для полного планирования соответствующих измерений. Подробное рассмотрение этих вопросов наняло бы добрую половину книги и явилось бы бесполезным описанием принципов, которые гораздо лучше описаны в книгах по математике и другим наукам

Единственный новый аспект описанной здесь методики — это объединение естественнонаучных, математических и экономических принципов в единую процедуру планирования измерении, которая связывает эти принципы с существенно важными вопросами проектирования.

Изложенная методика может показаться чересчур осторожной инженерам и всем, кому часто приходится применять вычисления по пропорциональным шкалам к ситуациям, которые могут быть точнее представлены более простыми или более сложными шкалами измерения, примером чему может служить использование интервальной шкалы для измерения многомерных показателей теплового комфорта (метод «Морфологические карты»). Конечно, результирующие ошибки, вызванные неправильным выбором шкалы, могут оказаться и небольшими. Однако трудно узнать заранее, так ли это на самом деле, и возможны случаи, когда погрешности будут велики

Например, при подаче небольшого количества тепла затраты на отопление комнаты слабо зависят от погрешностей при выборе шкалы комфорта, но при неограниченной подаче тепла эта зависимость может быть очень сильной

Однако трудно узнать заранее, так ли это на самом деле, и возможны случаи, когда погрешности будут велики. Например, при подаче небольшого количества тепла затраты на отопление комнаты слабо зависят от погрешностей при выборе шкалы комфорта, но при неограниченной подаче тепла эта зависимость может быть очень сильной.

Эта дилемма возникает также и при попытке определить порядок приоритетов при загрузке различных типов столовой посуды на этапе 4 приведенного примера. Этот вопрос рассматривается в методах «Ранжирование и взвешивание» и «Составление технического задания».

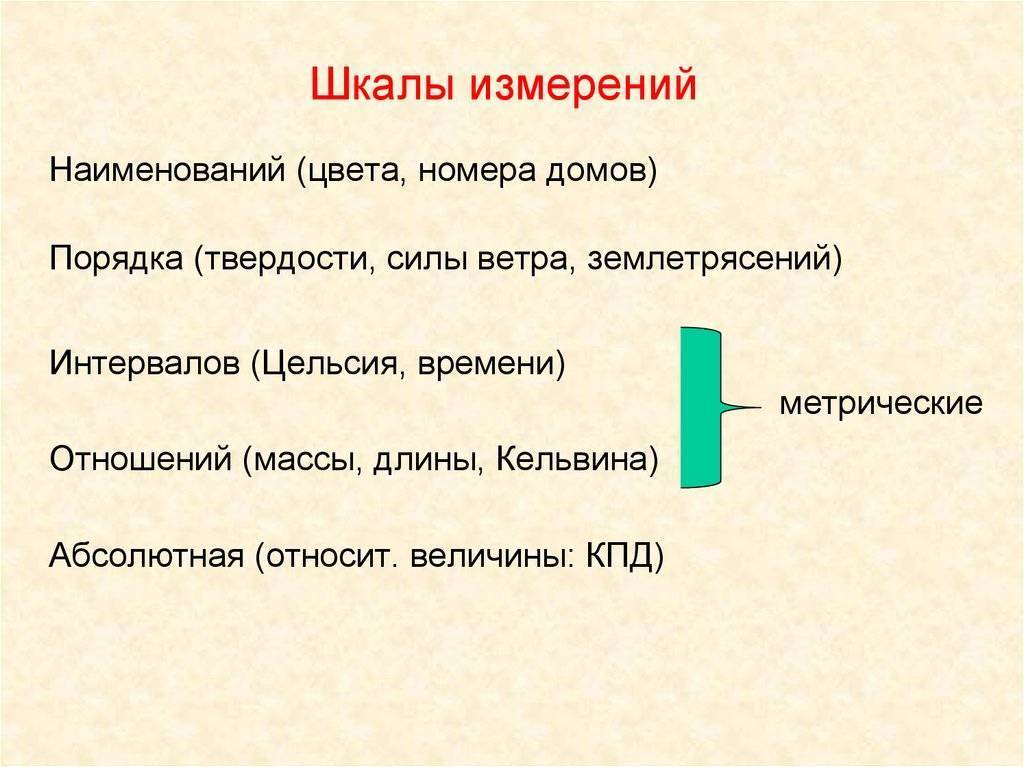
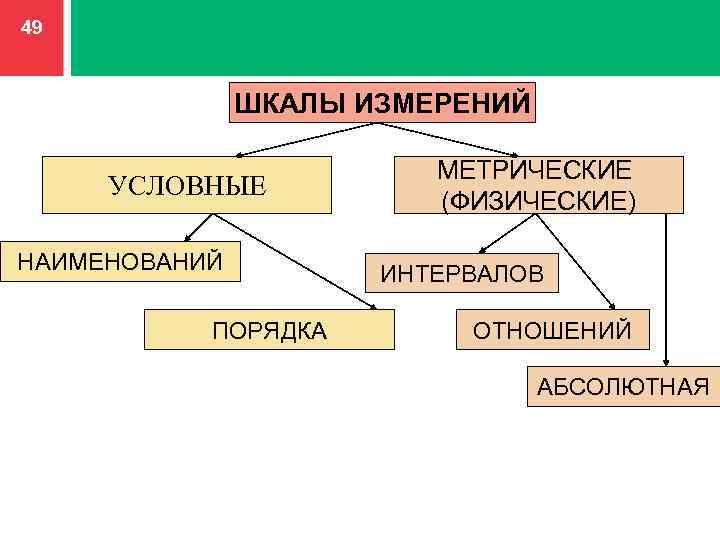
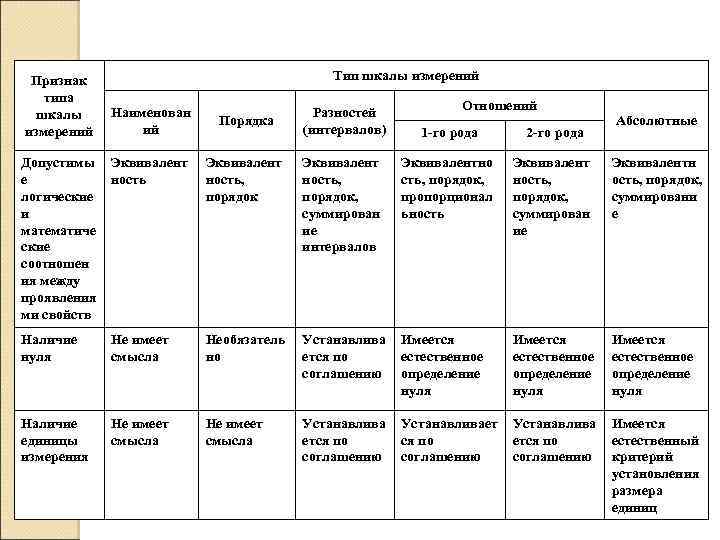
Шкалы измерений

Номинальная шкала

В шкале наименований допустимыми являются все взаимно-однозначные преобразования. В этой шкале числа используются как метки, только для различения объектов. В шкале наименований измерены, например, номера телефонов, автомашин, паспортов, студенческих билетов. Пол людей тоже измерен в шкале наименований, результат измерения принимает два значения – мужской, женский. Очевидно, что не имеет смысла складывать номера телефонов или умножать серии паспортов.

КДП: биективные преобразования.

Порядковая шкала

В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между объектами. Простейшим примером являются оценки знаний учащихся. Заметим, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе ровно тот же смысл выражается словесно – неудовлетворительно, удовлетворительно, хорошо, отлично. Этим подчеркивается “нечисловой” характер оценок знаний учащихся. В порядковой шкале допустимыми являются все строго монотонные преобразования.

КДП: все строго монотонные преобразования.

Шкала интервалов

По шкале интервалов измеряют величину потенциальной энергии или координату точки на прямой. В этих случаях на шкале нельзя отметить ни естественное начало отсчета, ни естественную единицу измерения. Исследователь должен сам задать точку отсчета и сам выбрать единицу измерения. Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования, т.е. линейные функции. Температурные шкалы Цельсия и Фаренгейта связаны именно такой зависимостью: °C = 5/9 (°F – 32), где °C – температура (в градусах) по шкале Цельсия, а °F – температура по шкале Фаренгейта.

КДП: все преобразования вида

Шкала отношений

В шкалах отношений есть естественное начало отсчета – нуль, но нет естественной единицы измерения. По шкале отношений измерены большинство физических единиц: масса тела, длина, заряд, а также цены в экономике. Допустимыми преобразованиями шкале отношений являются подобные (изменяющие только масштаб). Другими словами, линейные возрастающие преобразования без свободного члена. Примеры использования таких преобразований: пересчет цен из одной валюты в другую по фиксированному курсу, перевод массы из килограмм в фунты.

КДП: все преобразования вида

Шкала разностей

В шкале разностей есть естественная единица измерения, но нет естественного начала отсчета. Время измеряется по шкале разностей, если год (или сутки – от полудня до полудня) принимаем естественной единицей измерения, и по шкале интервалов в общем случае. На современном уровне знаний естественного начала отсчета времени указать нельзя. Допустимыми преобразованиями шкале разностей являются сдвиги.

КДП: все преобразования вида

Абсолютная шкала

Только для абсолютной шкалы результаты измерений – числа в обычном смысле слова. Примером является число людей в комнате. Для абсолютной шкалы допустимым является только тождественное преобразование.

КДП:

Измерение и качество продукции

Как уже было сказано ранее, если успешно решить вопросы, которые связаны с точностью измерения качественных параметров материалов и прочих изделий, а также поддержания режимов в технологии производства, качество продукции значительно улучшится. Если говорить простыми словами, контроль качества – это замеры всех параметров технологических процессов. Результаты их измерений нужны для управления процессом. Чем точнее результаты, тем лучше контроль.

У состояния измерений есть следующие основные свойства:

• Воспроизводимость измерительных результатов.
• Точность.
• Сходимость.
• Скорость получения.
• Единство измерений.

Воспроизводимость результатов – это близость измерительных результатов одной величины, которые были получены в различных местах, при помощи разных методов и средств, в разное время и разными людьми, но при одинаковых условиях (влажности, давлении, температуре).

Сходимость измерительных результатов – это когда результаты измерений одной величины, которые проводились повторно с помощью одних и тех же средств, тем же методом, в одних и тех же условиях, с одинаковой тщательностью, близки.

Любое измерение осуществляют с использованием соответствующих шкал.

Интервальная шкала

Интервальная шкала обладает метрическими свойствами — она характеризуется значением интервала и допускает арифметическое сложение.  

Интервальные шкалы часто называют шкалами высокого типа, количественными, числовыми. Смысл таких определений очевиден: числа, полученные с помощью шкал высокого типа, больше похожи на те числа, которые знакомы каждому из нас со школьной скамьи.  

Интервальная шкала обладает также характеристикой расстояния между отдельными градациями шкалы, измеряемого с помощью определенной единицы измерений. На этой шкале оцениваются разности между отдельными градациями шкалы и можно решить, равны они или нет, а если не равны, то какая из двух больше.  

Интервальная шкала обладает также характеристикой расстояния между отдельными градациями шкалы, измеряемого с помощью определенной единицы измерений, то есть используется количественная информация. На этой шкале уже не бессмысленны разности между отдельными градациями шкалы. В данном случае можно решить, равны они или нет, а если не равны, то какая из двух больше.  

Они представляют собой интервальные шкалы с естественным началом.  

Простейшим примером интервальной шкалы может служить шкала измерения температуры по Цельсию.  

При использовании интервальной шкалы адекватным является сравнение расстояний между парами одной и той же системы.  

Непрерывный континуум интервальной шкалы позволяет рассчитывать средневзвешенные величины, коэффициент дисперсии, характеризующий степень разбросанности признака. При этом средневзвешенные величины используются в качестве разного рода индексов, выполняющих функцию классификации, измерения и сравнения.  

Условием применения интервальной шкалы является регулярность классов интервалов.  

Если в интервальной шкале масштаб зафиксирован, то измерение происходит в шкале разностей. Шкала разностей допускает операции равенство-неравенство, больше-меньше, равенство-неравенство интервалов и операцию вычитания, на основе которой устанавливается величина интервала в фиксированном масштабе. К шкале разностей относятся логарифмические шкалы, а также процентные и аналогичные им шкалы измерений, задающие безразмерные величины.  

Измерения в интервальных шкалах в известном смысле более совершенны, чем в порядковых. Применение этих шкал дает возможность не только упорядочить объекты по количеству свойства, но и сравнить между собой разности количеств.  

Это справедливо для любых интервальных шкал.  

Если начало в интервальной шкале является абсолютной нулевой точкой, то возникает возможность отразить в шкале, во сколько раз одно измерение отличается от другого. Соответствующая шкала называется шкалой отношений.  

Частично-упорядоченное множество типов шкал, наиболее часто использующихся в социологических.

Наиболее типичные способы получения интервальной шкалы фактически описаны выше.  

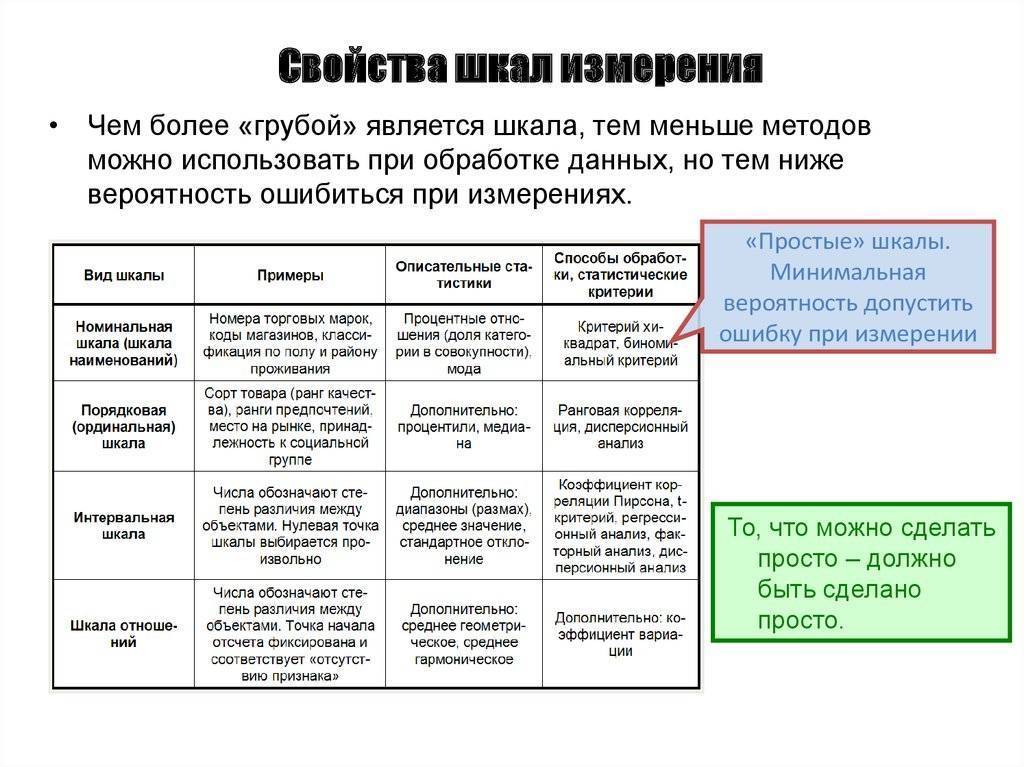
Свойства шкал

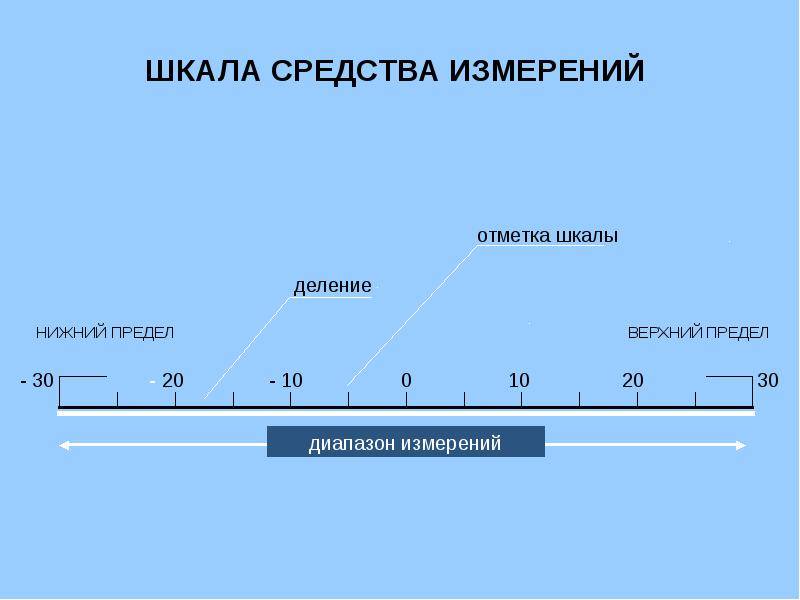
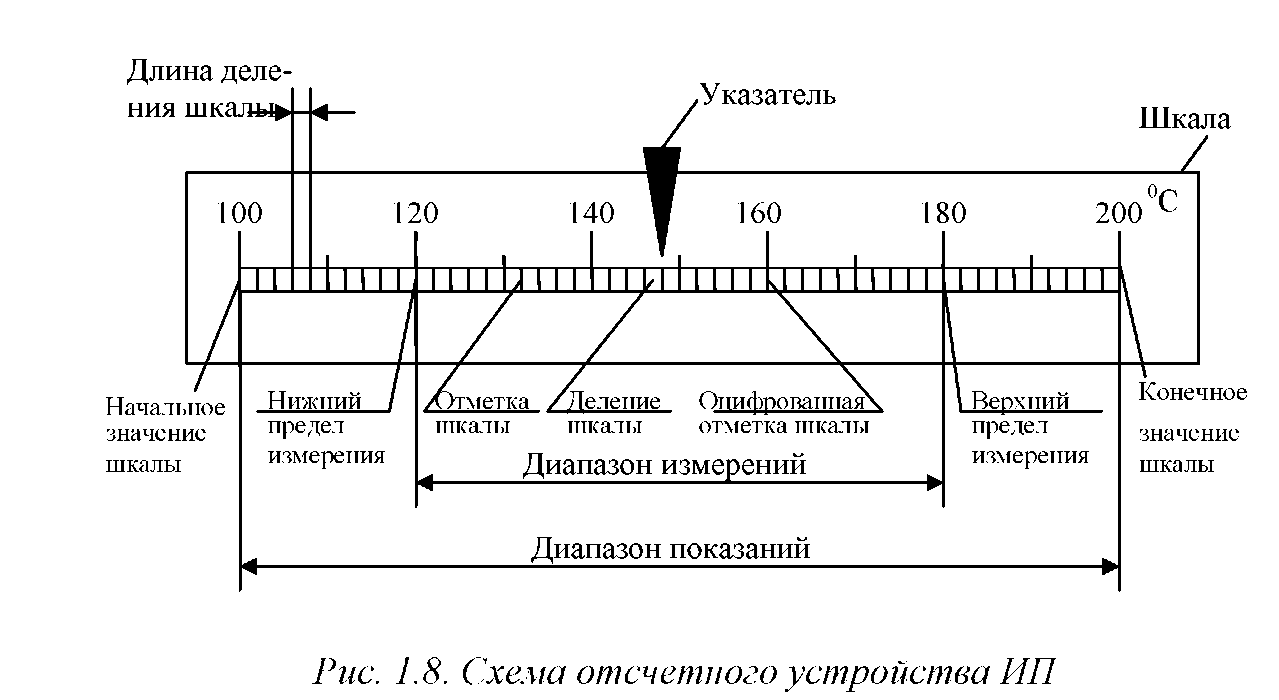
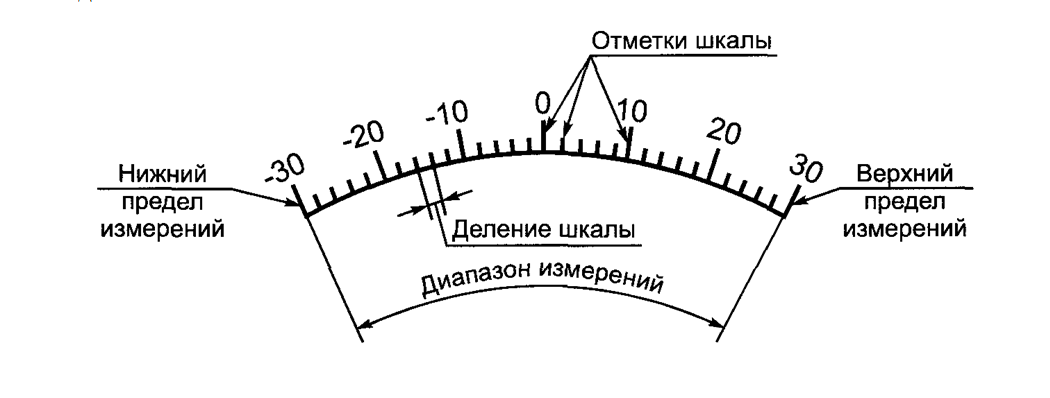
Неравномерная шкала омметра

• Начальное значение шкалы — наименьшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений. Во многих случаях шкала начинается с нулевой отметки, однако могут быть и другие значения — например, у медицинского термометра это 34,3 °C.
• Конечное значение шкалы — наибольшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений.
• Характер шкалы — функциональная зависимость a = f(x) между линейным (или угловым) расстоянием a какой-либо отметки от начальной отметки шкалы, выраженным в долях всей длины шкалы, и значением x измеряемой величины, соответствующим этой отметке:
  • Равномерная шкала — шкала, отметки на которой нанесены равномерно.
  • Неравномерная шкала — шкала, отметки на которой нанесены неравномерно.
  • Логарифмическая или гиперболическая шкала — шкала с сужающимися делениями, характеризуемыми тем, что отметка, соответствующая полусумме начального и конечного значений, расположена между 65 и 100 % длины шкалы. Следует заметить, что выражение «логарифмическая шкала» используется и по отношению к другому значению понятия «шкала» (см.: Шкала физической величины, Логарифмический масштаб).
  • Степенная шкала — шкала с расширяющимися или сужающимися делениями, но не подпадающая под определение логарифмической (гиперболической) шкалы.

Шкала интервалов (разностей)

Эти шкалы измерений в метрологии являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. Пример шкалы интервалов — летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.

Рисунок – Пример шкалы интервалов (Температурные шкалы Цельсия и Фаренгейта)

На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.

Шкала интервалов величины Q описывается уравнением Q = Qо + q, где q — числовое значение величины; Qо — начало отсчета шкалы;  — единица рассматриваемой величины. Такая шкала полностью определяется заданием начала отсчета Qо шкалы и единицы данной величины .

Задать шкалу практически можно двумя путями. При первом из них выбираются два значения Qо и Q1, величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q1 ~ Qо) — основным интервалом. Точка Qо принимается за начало отсчета, а величина (Q1 -Qо)/n= за единицу Q. При этом n выбирается таким, чтобы было целой величиной.

Рисунок – Пример шкалы отношений

При втором пути задания шкалы единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирают каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода — шкала времени, в которой 1с = 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.

Шкала отношений

Шкала отношений описывает свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода — аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). Пример шкалы отношений — шкала массы (второго рода), термодинамической температуры (первого рода).

В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения этот вид шкал измерений является шкалой интервалов с естественным началом отсчета

К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерений физических величин

Рисунок – Пример абсолютной шкалы (шкала температур Кельвина)

Шкалы отношений — самые совершенные. Они описываются уравнением Q = q, где Q — ФВ, для которой строится шкала, — ее единица измерения, q — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1/.

Соотношение

Шкалы коэффициентов являются конечной нирваной, когда речь заходит о шкалах измерения данных, потому что они говорят нам о порядке, они говорят нам точное значение между единицами, И они также имеют абсолютный нуль, который позволяет применять широкий спектр как описательных, так и предпочтительных статистических данных.  Рискуя повториться, все, что было сказано выше о интервальных данных, относится к шкалам коэффициентов, плюс шкалы коэффициентов имеют четкое определение нуля.  Хорошими примерами переменных коэффициентов являются рост, вес и продолжительность.

Шкалы коэффициентов предоставляют массу возможностей, когда речь заходит о статистическом анализе. Эти переменные можно осмысленно добавлять, вычитать, умножать, делить (соотношения). Центральная тенденция может быть измерена по режиму, медиане или среднему значению; меры дисперсии, такие как стандартное отклонение и коэффициент вариации, также могут быть рассчитаны по шкалам коэффициентов.

Шкалы коэффициентов являются определяющей нирваной в отношении шкал оценки информации, поскольку они просветляют нас в отношении запроса, раскрывают нам точный стимул между единицами, и они также имеют прямой нуль, который принимает во внимание широкий спектр как графических, так и преимущественных представлений, которые должны быть применены. При опасности перефразировать себя, все вышеперечисленное о промежуточной информации относится к пропорционным шкалам, в дополнение к пропорционным шкалам, которые имеют безошибочное значение “ноль”. Подлинные примеры факторов пропорций включают в себя рост, вес и продолжительность

Подлинные примеры факторов пропорций включают в себя рост, вес и продолжительность.

Пропорциональные шкалы дают обилие потенциальных результатов в отношении поддающегося измерению расследования. Эти переменные могут быть значимо добавлены, вычтены, умножены, разделены (соотношения). Очаговое наклонение можно оценить по способу, середине или среднему значению; пропорции рассеяния, например, стандартное отклонение и коэффициент разнообразия также могут быть определены по шкалам пропорций.

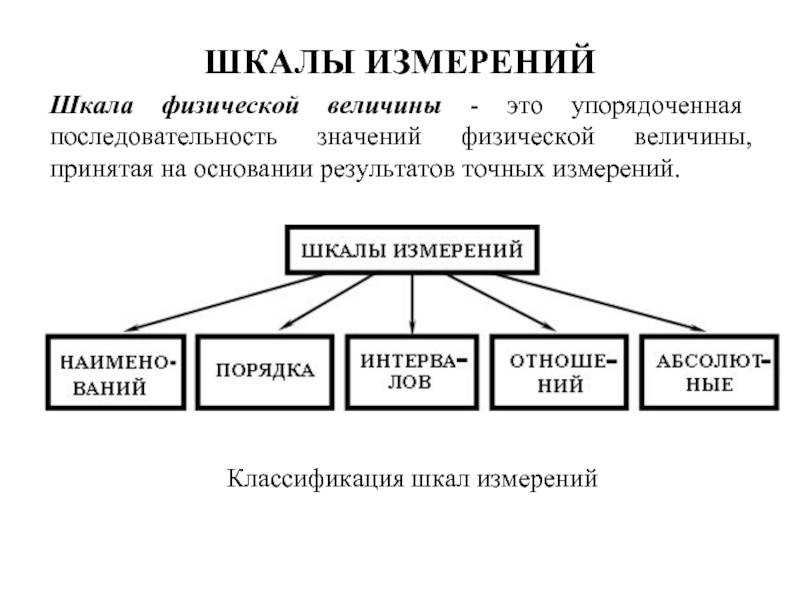
Шкалы и их классификации

Шкалы используются как для первичных измерений, так и для перевода разных измерений (в нашем случае — различных показателей) в единую шкалу. Как выбрать единую шкалу? Начнём с трёх определений.

Шкалой называют систему чисел или иных элементов и отношений между ними, принятых для измерения или оценки каких-либо величин (объектов, качеств и т. д.).

Шкалирование — это:

• выбор шкалы для первичных измерений;
• перевод измерения из одной шкалы в другую.

Нормирование (или единообразное шкалирование) — это перевод всех переменных, показателей, отражающих разные объекты измерений, в одну шкалу.

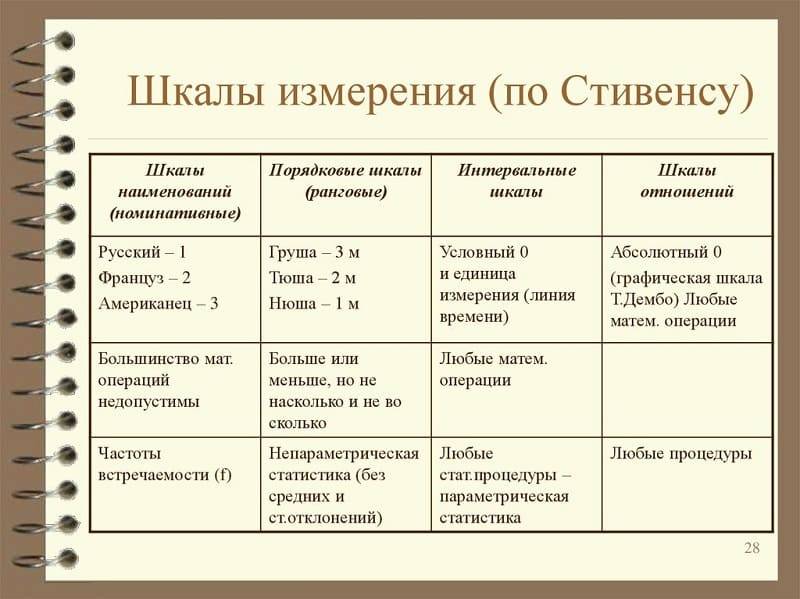
Первая классификация шкал была предложена С. Стивенсом в 1946 г. и от современной общепринятой классификации принципиально не отличается. Шкалы, как правило, объединяют в три основные группы:

• номинальные — для качественных измерений;
• порядковые — для отражения отношения порядка (больше, лучше, важнее, проще, правильнее и т. п.);
• количественные — оперируют с числами так, как мы привыкли со школьных времен (например, 10 в 2 раза больше, чем 5).

Иногда все шкалы измерения делят на два класса:

• шкалы качественных признаков (порядковая шкала и шкала наименований);
• шкалы количественных признаков (количественные шкалы).

Далее мы последовательно разберём все типы шкал.

Как считать очки в десятиборье?

Сегодня в мужском легкоатлетическом десятиборье за удачное выступление в каждом виде спорта участнику начисляется около 1000 очков. Но какой результат, по вашему мнению, берётся за 1000? Первое, что приходит на ум, — взять за 1000 очков мировой рекорд для женщин. Но какой именно? Текущий не годится, так как он меняется, а хотелось бы иметь возможность сравнений во времени и измерять рекорды. Но допустим, мы зафиксируем раз и навсегда, за что дается 1000 очков: в прыжках в длину, например, за 7,90 м, в беге на 100 метров — за 11 секунд. Далее возникает другой вопрос: какой шаг указать? Результат 8,00 м в прыжках в длину — это 1050 или 1010 очков? И как справедливо сравнивать разные виды соревнований? Думается, у каждого специалиста будут на этот счёт своё мнение и своя шкала.

Примечания

1. Журавлев Ю.И., Рязанов В. В., Сенько О. В. «Распознавание». Математические методы. Программная система. Практические применения. — М.: Фазис, 2006. ISBN 5-7036-0108-8.
2. ↑ Анфилатов В. С., Емельянов А. А., Кукушкин А. А. Системный анализ в управлении. — М. Финансы и статистика, 2002. — 368 с.
3. Перегудов Ф. И., Тарасевич Ф. П. Введение в системный анализ. — М.: Высшая школа, 1989. — 367 с.
4. ↑ Бахрушин В.Є. Методи аналізу даних. — Запоріжжя, КПУ, 2011
5. ↑
6. Mosteller, Frederick. Data analysis and regression : a second course in statistics (англ.). — Reading, Mass: Addison-Wesley Pub. Co, 1977. — ISBN 978-0201048544.
7. Wolman, Abel G. Measurement and meaningfulness in conservation science (англ.) // Conservation biology : journal. — 2006.
8. . Institute for Digital Research and Education. University of California, Los Angeles. Дата обращения: 7 февраля 2016.
9. Суппес П., Зиннес Д. Основы теории измерений // Психологические измерения. М.: 1967. С. 9-110.

Вывод

Таким образом, стало понятно, что такое шкала измерений и для чего она используется. Как выяснилось, она не одна. Их пять, и каждая используется для измерения определенных величин. Если раньше казалось, что шкала должна измерять только физические величины, то оказывается, в таких науках, как психология и социология, тоже есть свои шкалы, которые измеряют числовые показатели. По сути, психологический тест тоже является такой шкалой.

Измеряемая величина называется переменной, а то, чем производится измерение – инструментом. В результате получаются данные либо результаты, которые могут быть различного качества и относиться к одной из шкал. Каждая из них ставит ограничения на использование каких-то математических операций.