Деформация кручения

Закон Гука

От чего же зависит сила упругости? Роберт Гук, современник Ньютона, ответил на этот вопрос (рисунок 8).

Рисунок 8. Английский физик и изобретатель Роберт Гук (1635-1703). Установил зависимость силы упругости от деформации тела

Рассмотрим опыт, изображенный на рисунке 9. 

Рисунок 9. Опыт на определение зависимости силы упругости от деформации тела.

У нас есть штатив, к которому мы прикрепим резиновый шнур. Измерим его длину и обозначим как $l_0$.

Далее подвесим к шнуру чашку с гирей. Шнур удлинится. Снова измерим его длину — теперь она имеет значение $l$.

Шнур изменил свою длину после наших действий. Это изменение (удлинение шнура) мы можем найти по формуле:$\Delta l = l- l_0$,где $\Delta l$ — изменение длины. Знак $\Delta$ (греческая буква “дельта”) используется как символ для обозначения изменения между значениями какой-либо величина.

Если мы будем менять гири на чашке, то будет меняться длина шнура, то есть его удлинение (деформация) $\Delta l$.

Так мы подошли к закону Гука. Как он формулируется?

Здесь $\Delta l$ — изменение длины тела, $k$ — коэффициент пропорциональности, который называется жесткостью. Жесткость тела зависит от материала, формы и размеров тела.

{"questions":[{"content":"К одной и той же пружине по очереди подвешивают 2 груза.<br />С первыми грузом пружина удлинилась на 6 см.<br />Со вторым грузом пружина удлинилась на 13 см.<br />В каком случае силу упругости была больше?`choice-1`","widgets":{"choice-1":{"type":"choice","options":,"explanations":,"answer":}},"hints":[]}]}

Расчет винтовых цилиндрических одножильных пружин растяжения и сжатия.

Рассмотрим расчет винтовых цилиндрических одножильных пружин растяжения и сжатия. Основные геометрические параметры винтовых цилиндрических пружин из проволоки круглого поперечного сечения (см. рис. 1): d — диаметр проволоки; Dн и D — наружный и средний диаметры пружины; c=D/d — индекс пружины; t — шаг пружины; α — угол подъема витков; L0 — длина развернутой пружины (без учета зацепов пружины). Податливость пружины прямо пропорциональна ее индексу c. Для увеличения податливости пружины индекс с принимают возможно большим; практически c=4…12. Значения индекса с пружины принимают в зависимости от диаметра проволоки:

d, мм	< 2,5	3…5	6…12
c	5…12	4…10	4…9

Рис. 1 С увеличением индекса пружины той же жесткости можно сократить ее длину путем увеличения диаметра, а с уменьшением индекса можно уменьшить диаметр пружины путем увеличения ее длины.Рис. 2 В любом поперечном сечении витка пружины растяжения или сжатия при работе возникают (рис. 2, а) сила F, направленная по осевой линии пружины, и момент М=FD/2, вектор которого перпендикулярен осевой линии пружины. Сила F раскладывается на поперечную F1=F cos α и продольную F2=F sin α силы. При разложении момента М по осевой линии витка пружины и перпендикулярному ему направлению в поперечном сечении проволоки пружины возникают: крутящий T=FD cos α/2 и изгибающий Ми=FD sin α/2 моменты. Так как угол α<10…12°, то изгибающий момент Ми значительно меньше крутящего Т, а продольная сила F2 значительно меньше поперечной силы F1 но, как показывают расчеты, касательные напряжения сдвига значительно меньше касательных напряжений кручения, поэтому для упрощения расчета пружин на прочность обычно учитывают лишь крутящий момент T, при этом приближенно принимают cos α=1, т. е. T=М=FD/2. Таким образом, расчет винтовой цилиндрической пружины растяжения или сжатия из проволоки круглого поперечного сечения производят по формуле

где τ — расчетное максимальное напряжение в поперечных сечениях витков пружины; — допускаемое напряжение для проволоки пружины; k — коэффициент влияния на напряжение кривизны витков и поперечной силы; F — максимальная растягивающая или сжимающая сила. Формулой пользуются при проверочном расчете пружины, когда ее размеры известны. Значения коэффициента k принимают в зависимости от индекса пружины:

c	4	5	6	8	10	12
k	1,37	1,29	1,24	1,17	1,14	1,11

Рис. 3 Допускаемое напряжение пружин при статических нагрузках можно принимать по графикам (рис. 3), где отдельные кривые относятся к пружинам из проволоки:

• 1 — вольфрамовой и рояльной;
• 2 — хромованадиевой;
• 3 — углеродистой, закаленной в масле;
• 4 — углеродистой холоднотянутой;
• 5 — моиель-металла;
• 6 — фосфористой бронзы;
• 7 — специальной латуни.

При пульсирующей нагрузке с небольшим числом циклов допускаемые напряжения следует принимать в 1,25…1,5 раза ниже, чем по графикам.

При проектировочном расчете пружины диаметр проволоки

значением индекса с пружины задаются. Диаметр d проволоки, вычисленный по формуле, окончательно согласовывают с соответствующим ГОСТом для пружинной проволоки.

Средний диаметр D пружины и наружный диаметр DH определяют по формулам

и

При расчетах различают следующие силы пружины (см. рис. 1 , а, б): при предварительной деформации — F1 при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме) — F2; при максимальной деформации «(допускаемой) — F3. Соответственно в формулах F=F3.

Обычно пружину устанавливают с действующей на нее начальной нагрузкой F1=(0,1…0,5)F2. Максимальная сила пружины F3=(1,05..,1,66)F2. При изменении силы пружины от F1 до F2 жесткость пружины

где h — рабочий ход пружины, значение которого назначают или вычисляют по условиям работы механизма. Жесткость одного витка пружины где G — модуль сдвига материала проволоки пружины. Для стали G=80000 МПа и, следовательно, для стальной пружины где С1 — в Н/мм; d — в мм.

Число рабочих витков пружины

Полное число витков

где n2=1,5…2 — число опорных витков.

Деформация пружины

Подставив в формулу вместо F силы F1, F2, F3, получим деформации: λ1 — предварительную, λ2 — рабочую и λ3 — максимальную. Максимальная деформация одного витка пружины

Шаг пружины в ненагруженном состоянии: для пружины сжатиядля пружины растяжения Высота пружины при максимальной деформации

где n3 — число зашлифованных витков. Высота пружины в свободном состоянии для пружины сжатия для пружины растяжения

Высоту пружины при предварительной и рабочей деформации легко определить из (рис. 1, а, б). Длина развернутой пружины (без учета зацепов пружины растяжения)

Более подробный геометрический расчет винтовых цилиндрических пружин сжатия и растяжения из стальной проволоки круглого сечения дан в ГОСТ 13765-68.

Прочность и деформации

Несмотря на многообразие живого и неживого мира, на создание человеком многочисленных материальных объектов, у всех предметов и живых существ есть общее свойство — прочность. Под ней принято понимать способность материала сохраняться на протяжении длительного временного промежутка без видимых разрушений. Существует прочность конструкций, молекул, сооружений. Эта характеристика уместна для кровеносных сосудов, человеческих костей, кирпичной колонны, стекла, воды. Деформация сдвига – вариант проверки сооружения на прочность.

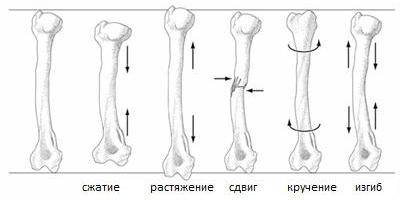
Применение разных видов деформаций человеком имеет глубокие исторические корни. Все начиналось с желания соединить между собой палку и острый наконечник, чтобы охотиться на древних животных. Уже в те далекие времена человека интересовала деформация. Сдвиг, сжатие, растяжение, изгиб помогали ему создавать жилища, орудия труда, готовить пищу. По мере развития техники человечеству удалось использовать различные виды деформаций так, чтобы они приносили весомую пользу.

Как возникает напряжение?

Все вещества состоят из атомов, представляющих собой положительно заряженное ядро, вокруг которого с большой скоростью кружатся более мелкие отрицательные электроны. В общем случае атомы нейтральны, так как количество электронов совпадает с числом протонов в ядре.

Однако если некоторое количество электронов отнять из атомов, то они будут стремиться притянуть такое же их количество, формируя вокруг себя плюсовое поле. Если же добавить электронов, то возникнет их избыток, и отрицательное поле. Формируются потенциалы – положительный и отрицательный.

При их взаимодействии возникнет взаимное притяжение.

Абрамян Евгений Павлович Доцент кафедры электротехники СПбГПУ

Чем больше будет величина различия – разность потенциалов – тем сильнее электроны из материала с их избыточным содержанием будут перетягиваться к материалу с их недостатком. Тем сильнее будет электрическое поле и его напряжение.

Если соединить потенциалы с различными зарядами проводников, то возникнет электрический ток – направленное движение носителей заряда, стремящееся устранить разницу потенциалов. Для перемещения по проводнику зарядов силы электрического поля совершают работу, которая и характеризуется понятием электрического напряжения.

Виды деформаций печатных плат

В процессе эксплуатации, печатные платы, как элементы конструкции, испытывают на себе воздействие внешних сил. Результаты их взаимодействия могут приводить к короблению.

Частными случаями данной деформации являются изгиб и кручение материала основания печатной платы.

Ниже, на рисунках 1 и 2 представлены каждый из указанных видов деформаций печатных плат.

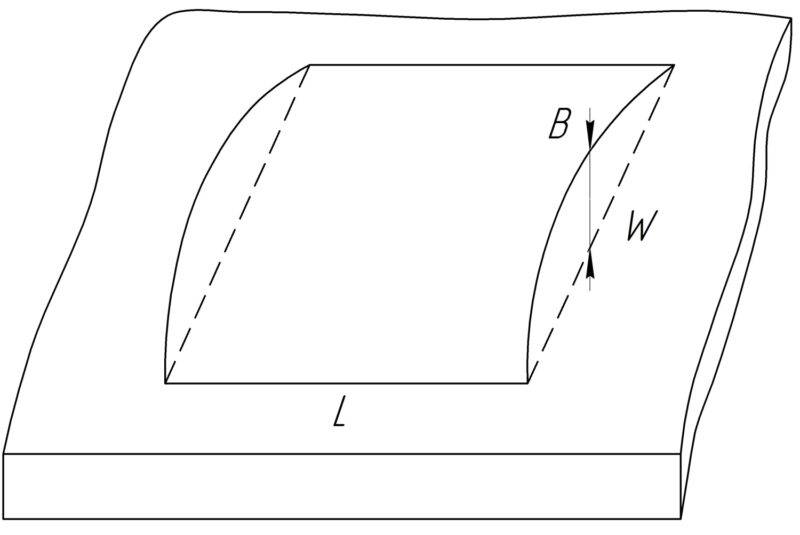Рисунок 1 – деформация изгиба печатной платы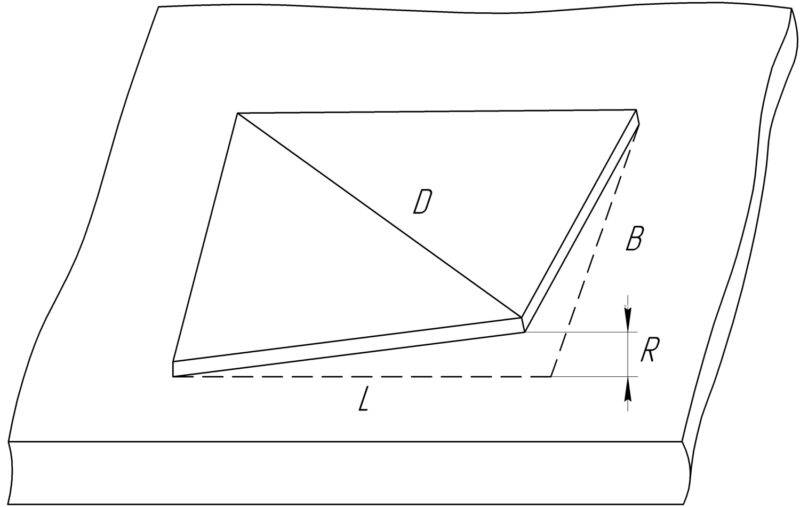Рисунок 2 – Деформация кручения печатной платы

Рассмотренные виды деформаций могут привести к ненадежности конструкции. Поэтому величина изгиба-кручения печатной платы строго регламентируется стандартами.

Стандарты нормирующие величину изгиба-кручения печатных плат

• ГОСТ 23752-79 Платы печатные. Общие технические условия. Отечественный стандарт, регламентирующий величины деформаций печатных плат;
• IPC-A-610F Критерии приемки электронных сборок (Acceptability of Electronic Assemblies). Стандарт Международной Профессиональной Ассоциации (IPC) определяющий допустимые величины изгиба-кручения печатных плат.

Следуя требованиям данных документов, отклонение от идеальной плоскостности должно лежать в определенных пределах. Данные значения называются допустимыми величинами деформаций печатных плат.

В таблице 1 приведены допустимые по ГОСТ 23752-79 величины деформации печатных плат на жестком основании. Данные параметры приведены на каждые 100 мм длины печатной платы.

Например, длина печатной платы равна 355 мм. Тогда нормированная допустимая величина деформации для соответствующей толщины печатной платы умножается на коэффициент 3,55.

Таблица 1 – Допустимые величины деформаций печатных плат в зависимости от количества слоев, материала основания печатной платы и её толщины.

Толщина ПП (мм)	Односторонние (бумага)	Односторонние (стеклотекстолит)	Двусторонние (бумага)	Двусторонние (стеклотекстолит)	Многослойные
1,0…1,5	1,5	0,9	0,9	0,8	0,5
свыше 1,5 до 2,0	1,2	0,8	0,6	0,6	0,1
свыше 2,0	0,9	0,6	0,5	0,5	0,1

Расчет допустимой величины деформации изгиба печатной платы

Согласно IPC ведется для каждой из сторон по формулам:

1. Rl=L*B/100%;
2. Rw=W*B/100%;

где

• L и W – длина и ширина печатной платы (мм);
• B – коэффициент допустимой деформации печатной платы.

Для плат с поверхностным монтажом B равен 0,75%; для всех остальных – 1,5%.

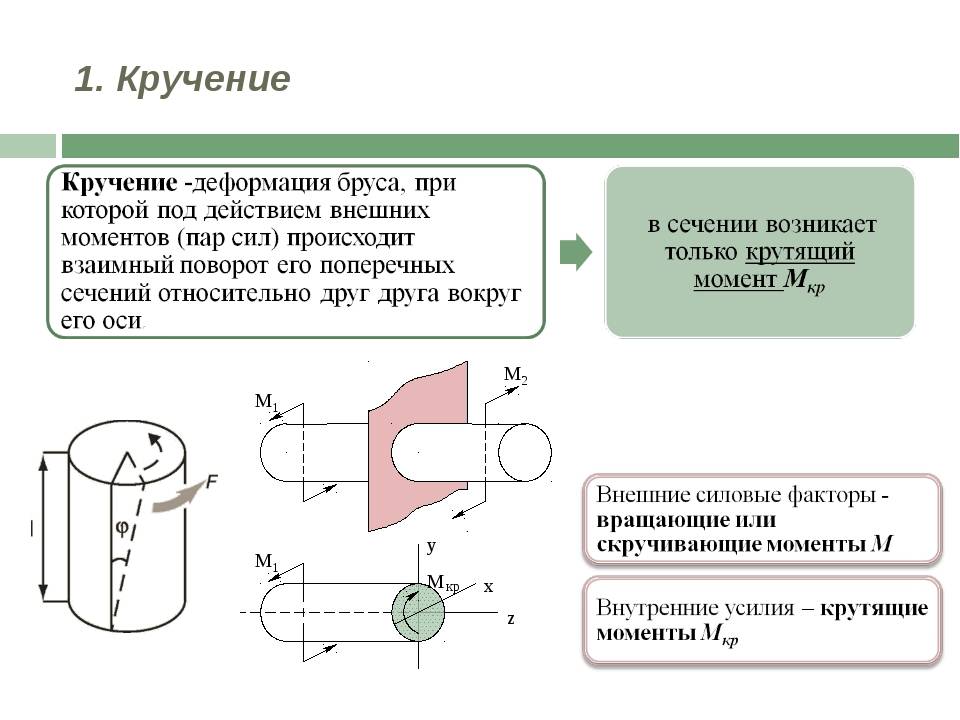
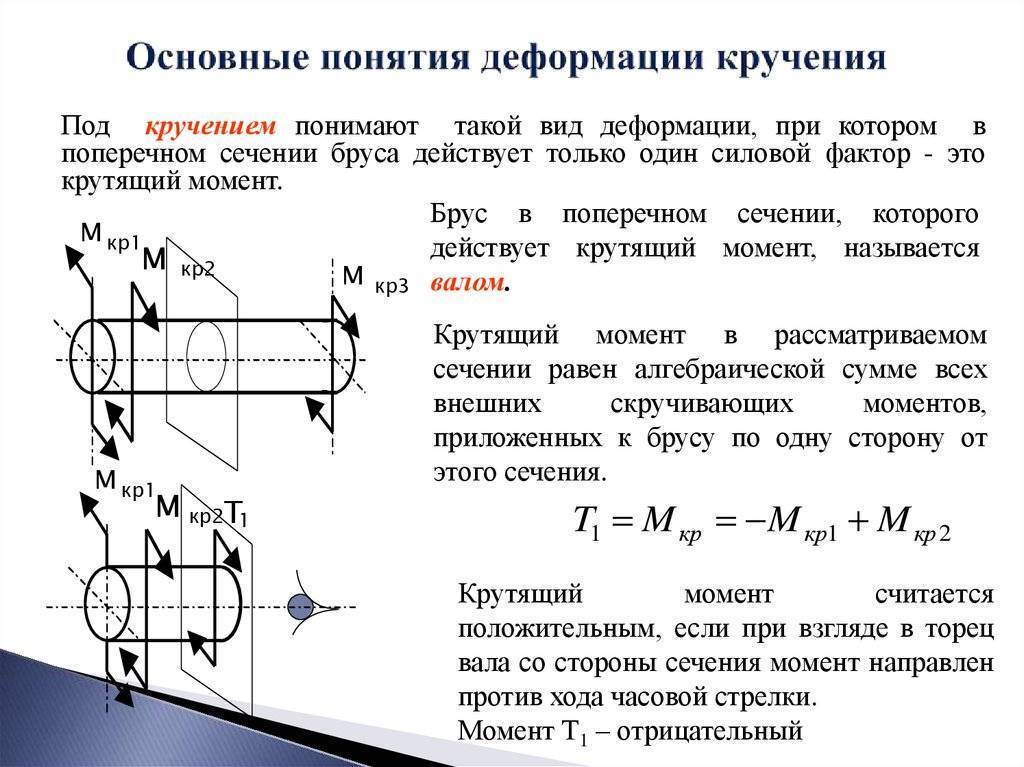
Напряжения кручения

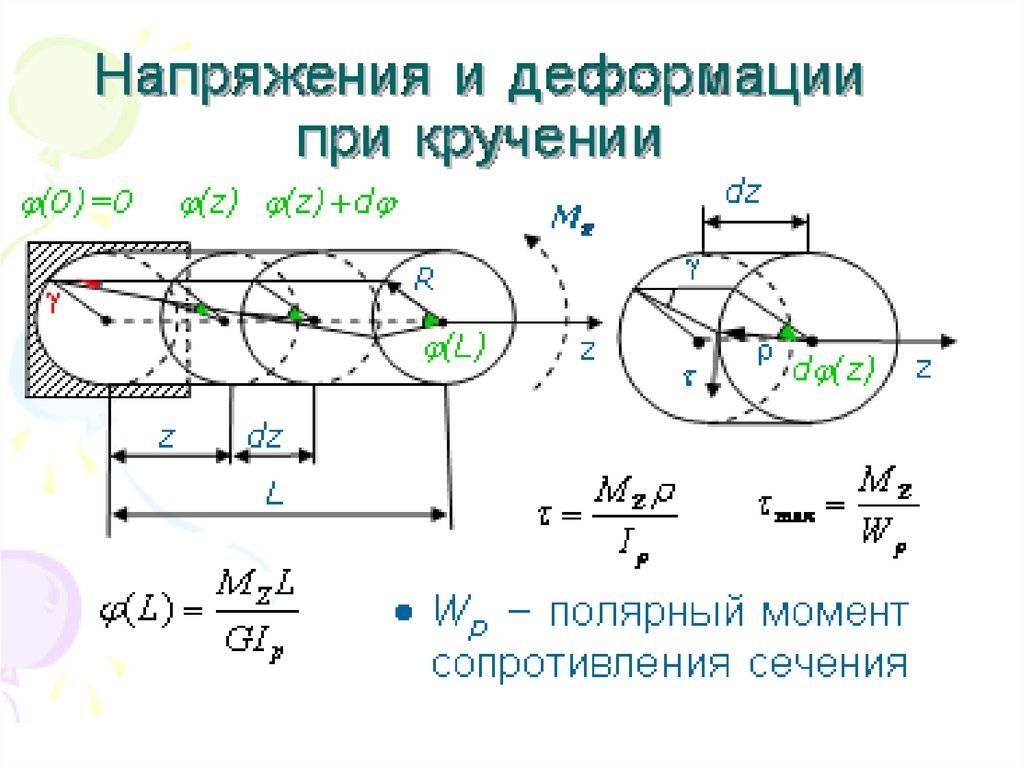
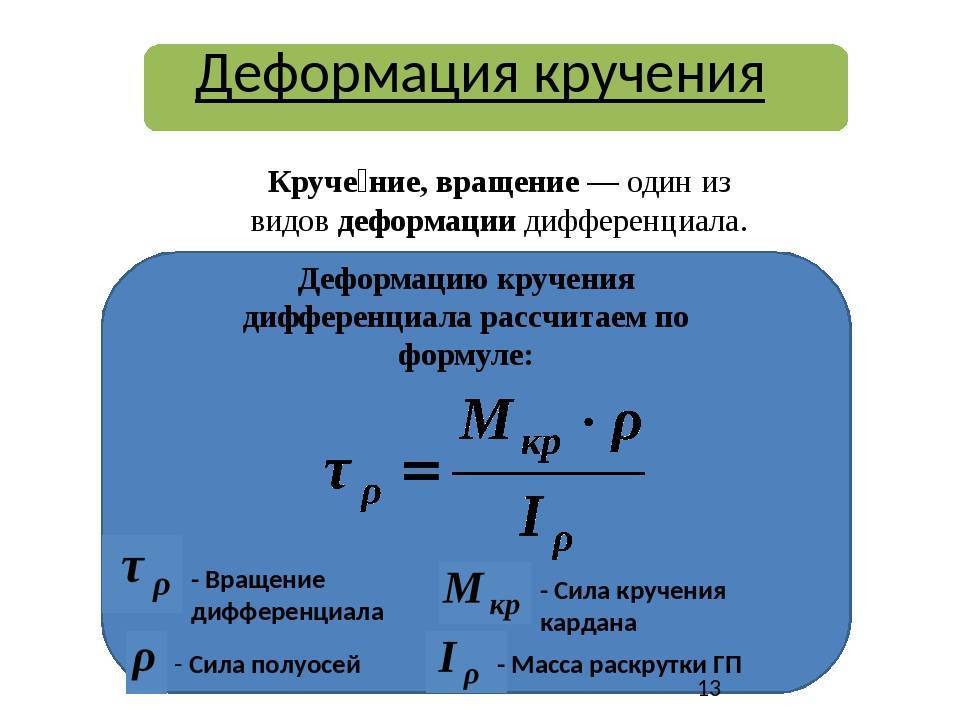
Исходя из вышеприведенного определения деформации кручения, при этом процессе в поперечном сечении наблюдаются лишь касательные напряжения, направлены перпендикулярно к радиусам. Их формируют для определенной точки как творение соотношения крутящего момента к геометрическому полярному инерционному моменту и расстояния этой точки от оси кручения.

Изменение касательных напряжения линейно, и самой большой величины они могут достигать на поверхности при самых больших значениях крутящего момента и расстояния от оси кручения, по этому ее значение вычисляют как приватное самого большого крутящего и полярного факторов сопротивления.

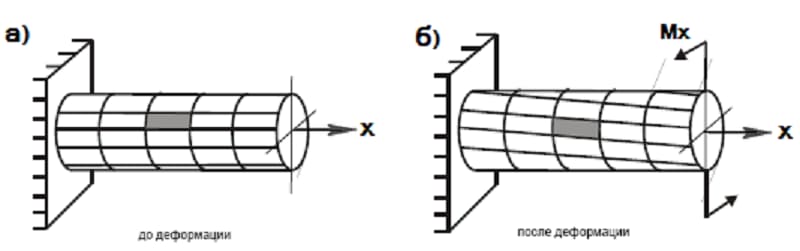
С использованием этого условия возможно определить другие параметры: по силовым факторам, создающим вращающий момент – критерий сопротивления и дальше размеры сечения все зависит от формы, либо по размерам сечения – максимально допустимое для него значение крутящего момента и на основе последней возможные значения внешних нагрузок.

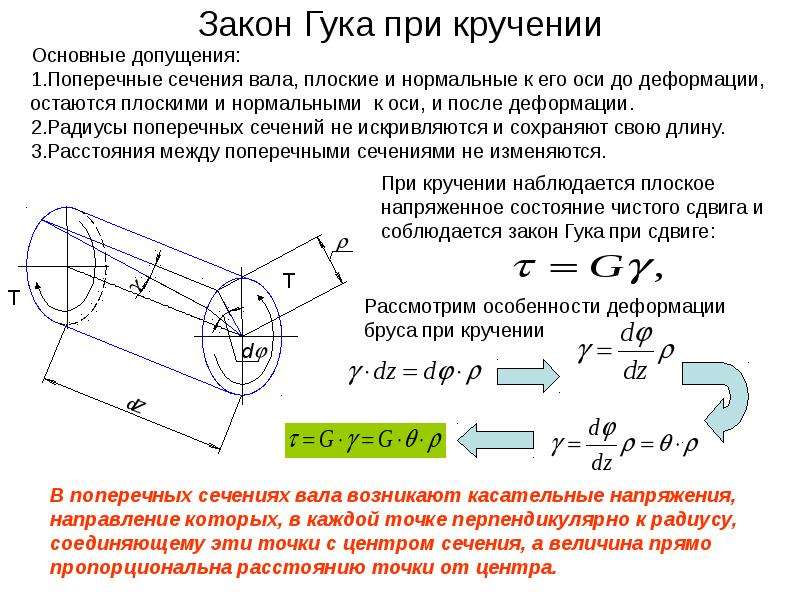
Касательные напряжения, согласно законодательству парности, возникают при кручении как в поперечных, так и в продольном направлениях. Благодаря этому во всех точках вала встречается дефармация в виде чистого сдвига. Основные напряжения направлены к создающей под угол 45°.

Кроме скручивающих усилий возможно влияние на вал моментной нагрузки.

Из изложенных выше данных следует, что убирание материала в районе оси вала несущественно проявляется на прочности благодаря тому, что эта часть мало нагружена. При равных площади сечения и массе деталей кольцевые варианты отличаются большими полярными моментами сопротивления и инерции если сравнивать со сплошными валами. Другими словами при равной массе пустотелые варианты крепче и жёстче, а при похожих показателях прочности и жесткости легче. Названные параметры формируют стойкость этих изделий к деформированию.

Выше были рассмотрены характерности деформации кручения круглых в поперечном разрезе предметов. Для треугольных, прямоугольных, эллиптических и других вариантов не применима догадка плоских сечений. Это вызвано тем, что поверхности этого типа при кручении искривляются. Этот процесс их коробления вследствие смещения некоторых точек при деформации вдоль оси называют депланацией. Благодаря этому методы сопротивления материалов для вычисления кручений и стрессов непригодны. Взамен них применяют методы теории упругости.

Для изделий произвольной поперечной формы касательные напряжения имеют направление по касательной к контуру, однако если есть наличие внешних углов они отсутствуют. Так, при разложении напряжения вблизи угла по нормалям к его сторонам пополам из закона парности следует формирование касательных стрессов на свободной поверхности. Однако в этом случае она свободна от нагрузки, по этому у внешнего угла касательные напряжения обнуляются.

Для самых популярных среди вариантов некруглого сечения прямоугольных валов самые большие напряжения свойственны для поверхностных участков в середине длинных сторон. Стало быть, там встречается самая большая дефармация кручения.

С прямыми углами детали если сравнивать с круглым отличаются существенно меньшими жесткостью и прочностью. Причем это отличие возрастает с увеличением отношения сторон. Стало быть, они более предрасположены к деформации.

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.

Рис.30

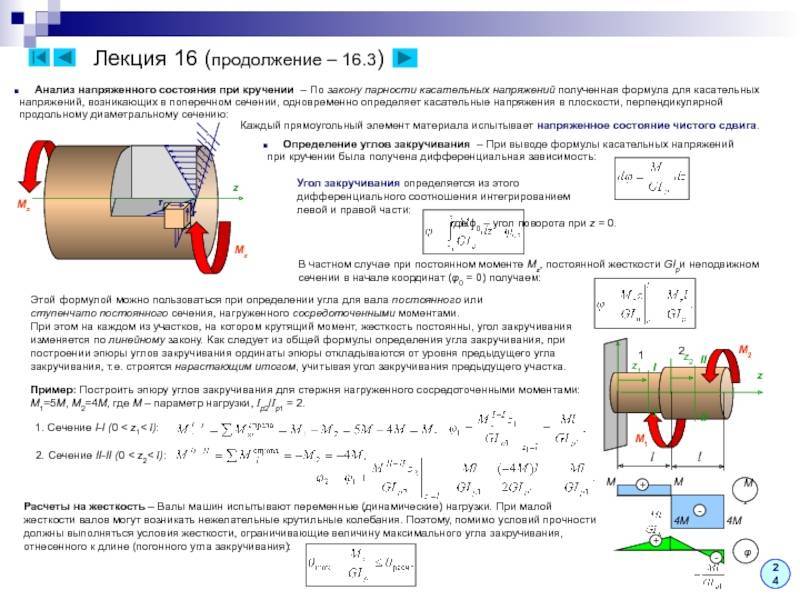
Таким образом, полученные при рассмотрении вопросов кручения валов
результаты позволяют сказать, что наиболее рациональными сечениями, обеспечивающими
максимум допускаемого крутящего момента при одинаковом расходе материала,
являются сечения круглые, особенно кольцевые при малой толщине стенок. Наименее
выгодные сечения – швеллеры, двутавры и другие прямоугольные сечения. Данный
вывод проистекает из того факта, что требуется обеспечивать при одинаковой
площади поперечного сечения как можно большее значение полярного момента
сопротивления W_ρ (или W_t  для некруглого сечения).

Деформация изгиба

Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.

В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.

Расчёты на крепость при сдвиге

Оценка характеристик прочности изделий выполняется для определения наступления трёх факторов деформации:

1. Смещение некоторых слоёв (возникновения угла деформации).
2. Смятие крепежных элементов.
3. Сдвиг.
4. Разрыв.

Расчёт на крепость нужен для определения условий наступления любого из видов. В работе для более наглядной оценки параметров прочности и стойкости к деформированию решают существующие аналитические выражения и изображают эпюры отражающие направления влияния разных видов стрессов.

Получение численных параметров возможно благодаря использованию разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений изготавливается на основе принятых гипотез.

Расчёт возможных стрессов изготавливается на основании первой, третьей и четвёртой гипотезы прочности. Любая из гипотез принимается для различных материалов, которые обладают собственными физико-механическими свойствами.

Крепость быть на каждом из этапов разработки определенной детали. В первую очередь вычисляют величины возможных стрессов и угол отклонения на предварительном (проверочном) шаге. Это дает возможность определить их уровни, величины и направление приложенных сил. После чего приступают к проектированию. На данном шаге выполняется подбор материала детали и элементов крепежа с учитыванием достаточной прочности любого элемента конструкции. На конечном шаге ещё один раз проверяют возможные нормы нагрузки и способность готовой детали держать допустимую и дополнительную нагрузку, другими словами формируют прочностный запас.

Наиболее показательными являются расчёты для чистого сдвига. В данном случае при расчёте рассматривают следующие моменты выполнения задачи:

• Статический (составляется уравнение равновесия). В данном случае применяется предположение о равномерности распределения касательных стрессов. Впрочем в определенных случаях они делятся не одинаково, что затрудняет решение установленной задачи. Он дает возможность установить связь возникших стрессов с действующими внешними силами. Это выполняться благодаря получению семейства решений дифференциальных уравнений равновесия для всего объёма детали.
• Геометрический (деформационный). Позволяет отобразить связь между отдельными маленькими участками исследуемой детали.
• Математический. Дает возможность подобрать метод решения составленной системы уравнений. Провести математическое моделирование протекающих процессов.
• Физический. Устанавливает связь между физическими процессами при деформации с учитыванием физических параметров материала и возникшими напряжениями (механическими качествами).

На математическом и физическом шаге рассмотрения установленной задачи используются следующие главные расчетные выражения и допущения:

• закон Гука для деформации смещения;
• гипотезы прочности (с учитыванием физических и механических параметров материала который для него выбран);
• выбор системы равноценных стрессов;
• упрощения при изображении эпюр, отображающих направления действующих сил и возникших стрессов;
• принятие ключевых положений для случая чистого сдвига.

В первом варианте происходит пластическая дефармация детали, когда интенсивность возникших стрессов превосходит предел текучести материала который для него выбран. Размер подобной деформации зависят от характера и интенсивности действия внешних сил, прочностных показателей материала, изменения режима температур.

При интенсивности влияния, превышающем крепость материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (к примеру, крепежных изделий, заклёпок, втулок).

Разработанные методы расчёта прочности дают возможность проектировать и делать детали с заданием, превышающим этот предел. Это дает возможность значительно повысить прочность и долговечность всей конструкции. Сейчас разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с использованием созданных программных средств, которые дают возможность получить числовые характеристики прочности и выстроить графические изображения эпюр в формате 3D графики.

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.

График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

Задачка 1

Определите по графику коэффициент жесткости тела.

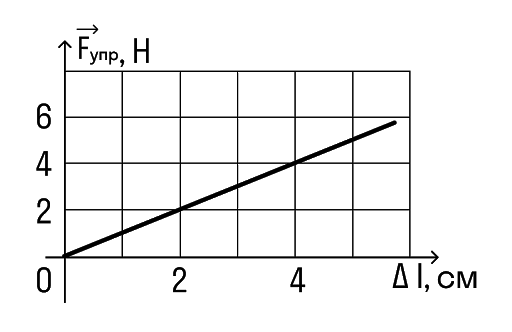
Решение:

Из Закона Гука выразим коэффициент жесткости тела:

F = kx

Снимем значения с графика

Важно выбрать одну точку на графике и записать для нее значения обеих величин

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры:

2 см = 0,02 м

И подставим в формулу:

=100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Задачка 2

На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.

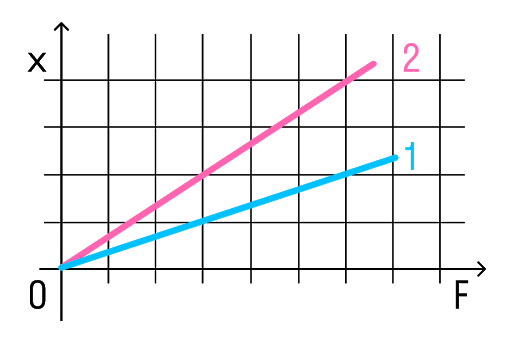
Решение:

Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.

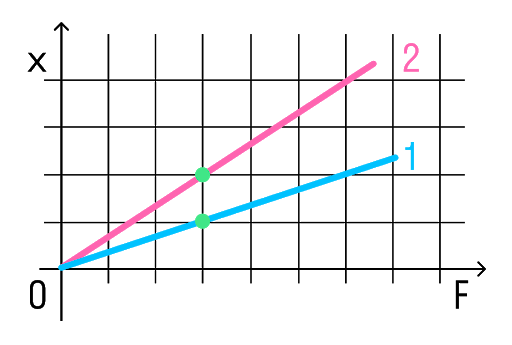
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.

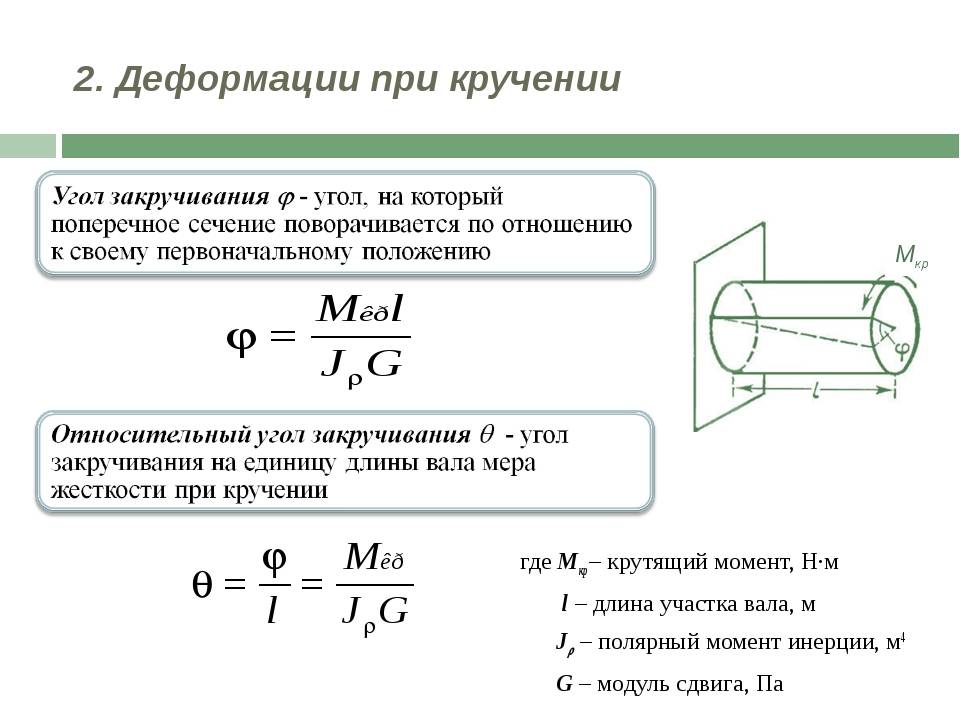
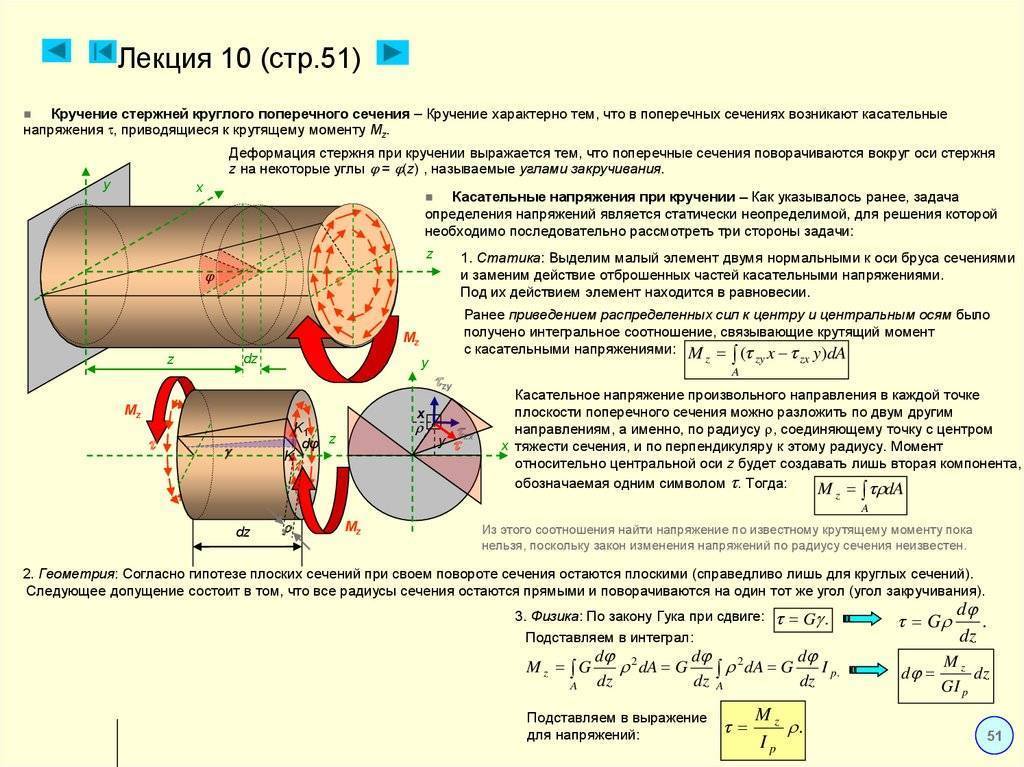
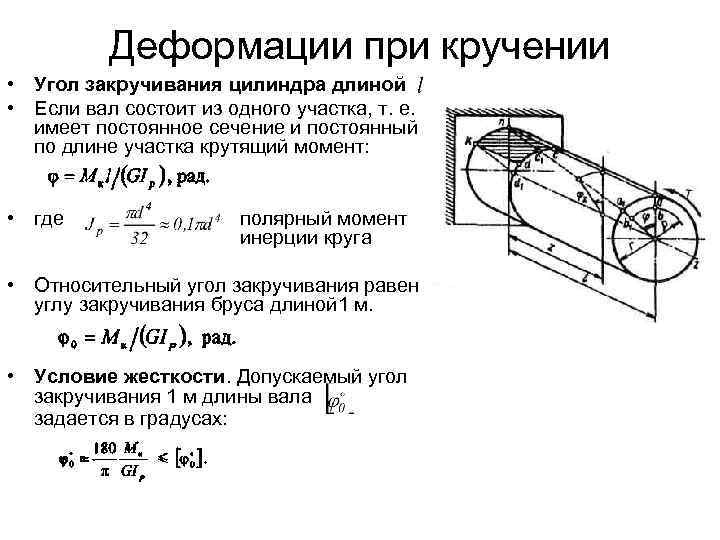
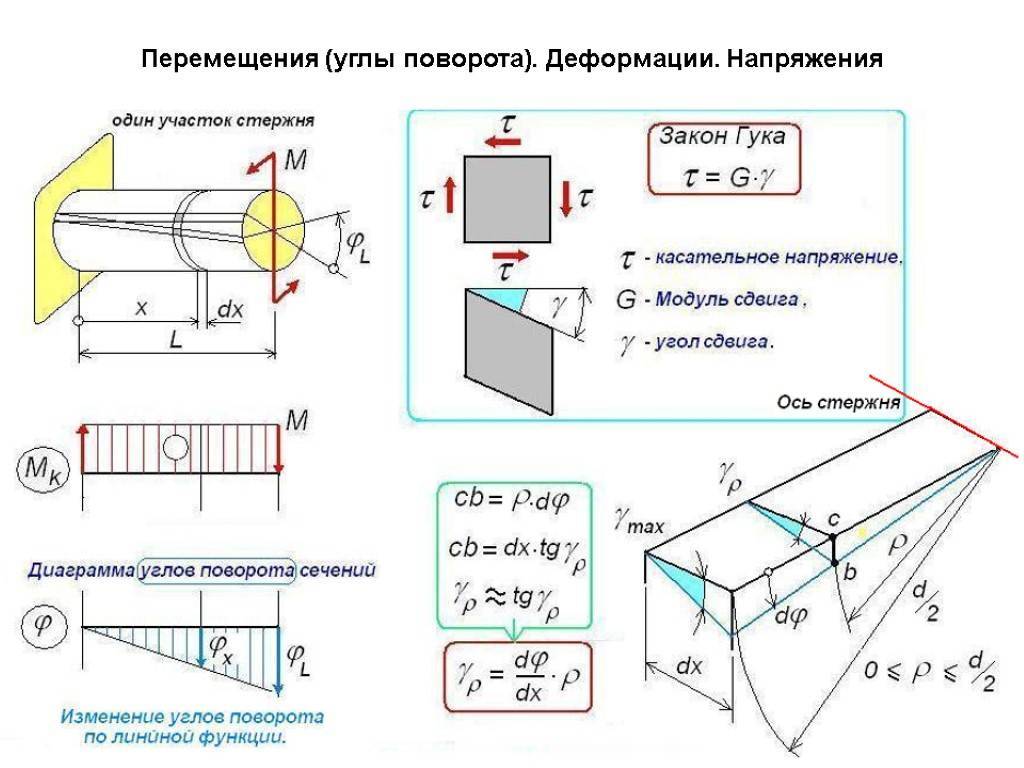
Определение деформаций при кручении

прочности[глава XI Для участка на расстоянии x от опорного участка мы показали этот угол поворота(рис. 122) скрученный угол называется символом<РЖ. Для его определения

вы получите его (с константой L4K): В зависимости от длины стержня I, наибольший угол закрутки равен. Между крайними поперечными сечениями (x-G): (11.18) Формула (11.18) имеет очень близкую форму к соответствующей формуле при растяжении или

сжатии. 71L » 1 Здесь уместно указать на физический смысл значения=—. Как видно из Формулы (11.18), чем меньше величина угла кручения CP (при этом L1K), тем больше жесткость изделия GJp—так называемого кручения. Таким образом, JP отражает влияние размеров поперечного сечения на крутильную деформируемость

стержня. Если существует вал, который делит несколько шкивов на скрученные секции различными моментами M K, то по уравнению (11.18) мы суммируем эти углы кручения алгебраически для каждой секции каждой секции, и мы получаем полный угол кручения для всего вала. Расчет угла кручения имеет двойное практическое значение: во-первых, необходимо определить опорную реакцию скрученного стержня в статически неопределенной системе.

Практика выработала самые высокие допустимые пределы для углов СР, которые нельзя пересекать, чтобы не получить нарушения работы машины. Эти пределы следующие: для каждого измерителя в нормальном состоянии=0,3°длина вала; при переменной нагрузке=0,25°; при внезапном (ударном) изменении нагрузки=0,15 в обычных условиях, если длина равна диаметру вала J, можно принять =1°). f) в последние годы в советском машиностроении допустимый угол закрутки

определяться не только из условий прочности (11.15), но и из условий жесткости: Эго-состояние часто приходит первым с длинным стержнем. Если вы проверите жесткость вала, вы увидите пример. П р и М Е Р34. Для задачи, решенной в § 59 (пример 33), проверьте значение угла поворота вала длиной/=1м \ модуль упругости будет равен (7=8 * Ю3 кг)!по формуле cm * (11.19) получаем: Это превышает допустимую норму 0,3°на 1ЛЧ. Для выполнения условия жесткости необходимо определить радиус оси из неравенства (11.19) ): Откуда Диаметр должен быть равен d=14,5 см.

Решение задач по сопротивлению материалов

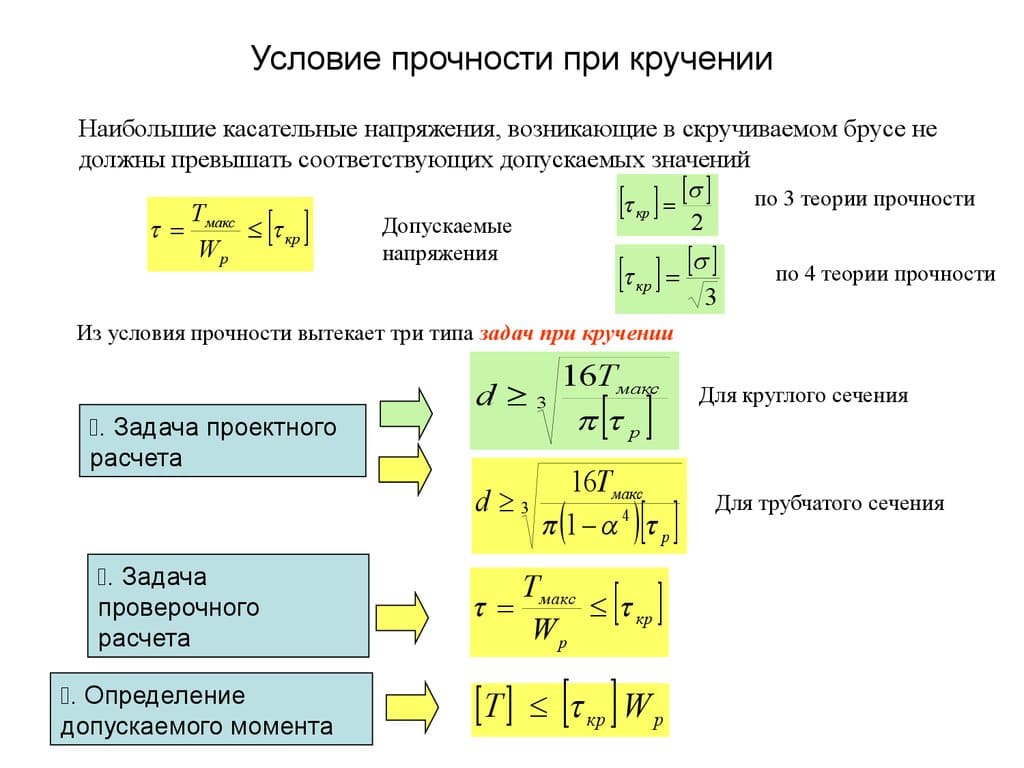
Вычисление полярных моментов инерции и моментов сопротивления сечения вала	Напряжения при кручении по сечениям, наклонённым к оси стержня
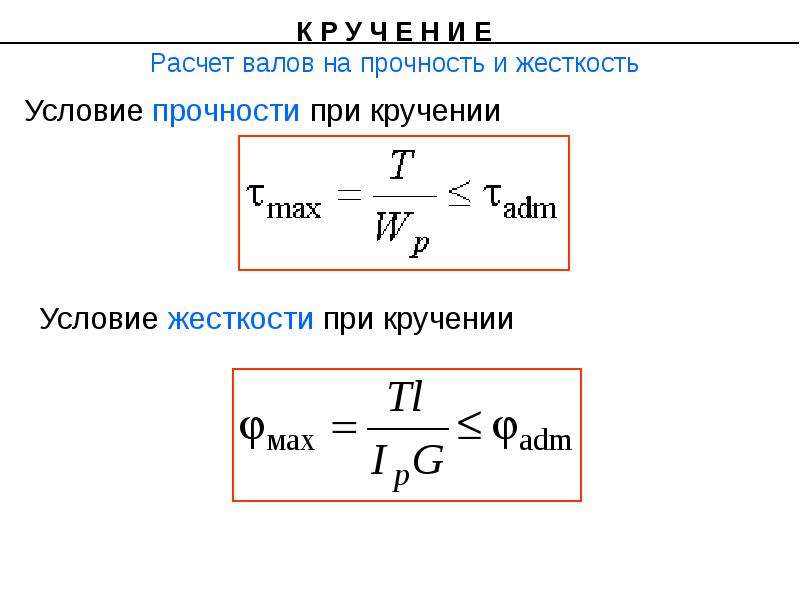
Условие прочности при кручении	Потенциальная энергия при кручении

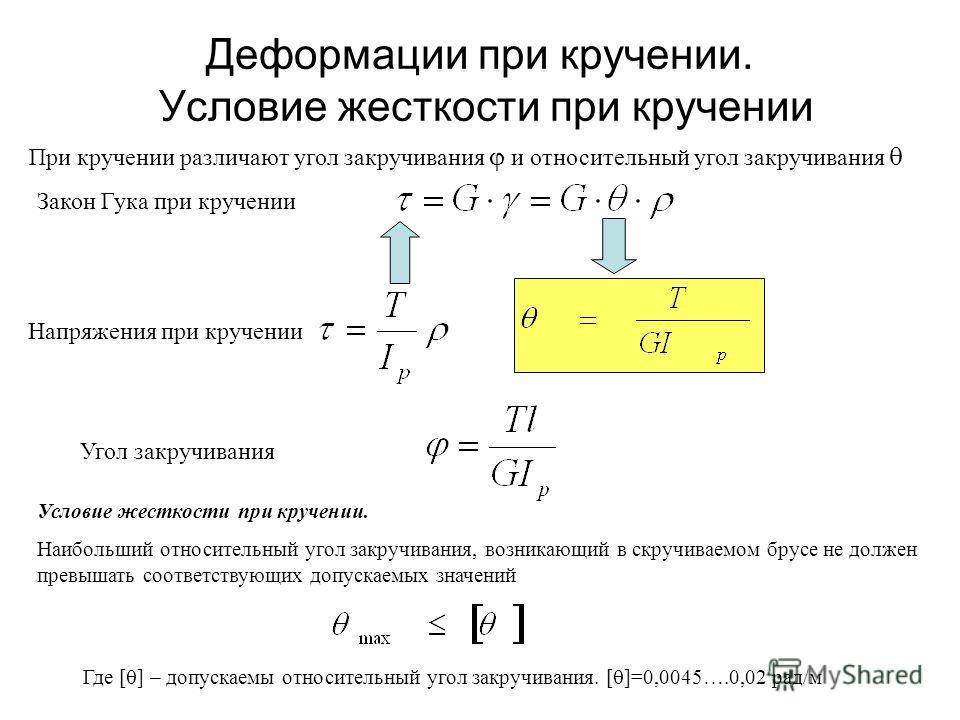
Напряжение при сдвиге

Воздействие внешней силы на грань приводит к возникновению в изделии изменения формы. Все напряжения делятся на две категории: нормальные и касательные. Нормальными считаются внутренние напряжения, возникающие в различных слоях изделия, подверженного деформации.

Напряжения и деформации при сдвиге описываются с применением аналитических выражений и графических изображений. Общее состояние описывается пространственным (трёхкоординатным) напряжением. Если в конкретном случае можно выявить сечения, в которых оба вида напряжений равны нулю, можно перейти к более простым моделям описания этого процесса. Ими являются двухкоординатное (плоское) напряжённое состояние или линейное. Две последних модели являются частными случаями трёхкоординатного напряжённого состояния.

Касательные напряжения являются мерой скольжения одного поперечного слоя относительно другого. В изменениях на поверхности каждого слоя возникают только касательные напряжения. Для оценки полной картины деформации используют следующие теоретические положения:

• закон парности касательных напряжений;
• вычисление экстремальных нормальных напряжений;
• определение всех тангенциальных напряжений.

Оценка их всех при деформации смещения позволят оценить прочность конструкции.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).

Одна пружина:

Две параллельные пружины:

Так как правые части уравнений совпадают, левые части тоже будут равны:

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

Умножим обе части полученного уравнения на число 2:

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).

Одна пружина:

Две последовательные пружины:

Так как правые части уравнений совпадают, левые части тоже будут равны:

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

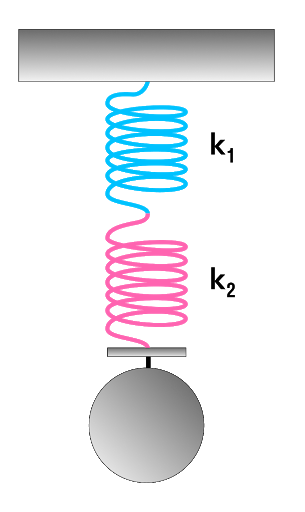
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Коэффициент жесткости при последовательном соединении пружин k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе

Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

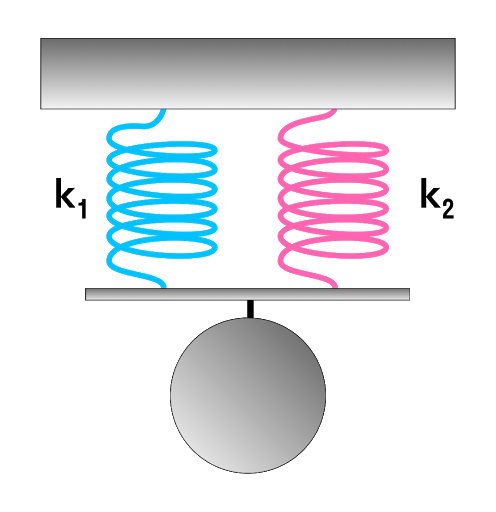
В случае когда пружины соединены параллельно величина общего коэффициента жесткости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Коэффициент жесткости при параллельном соединении пружин k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе

Задачка

Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.

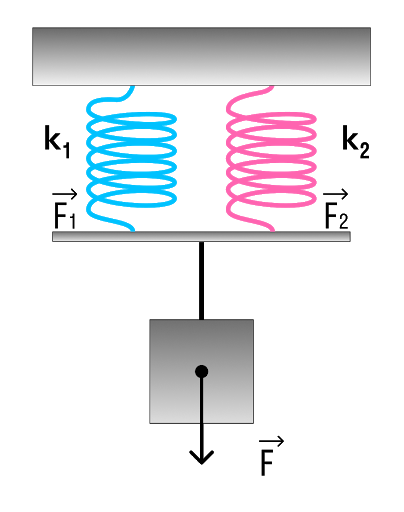
При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

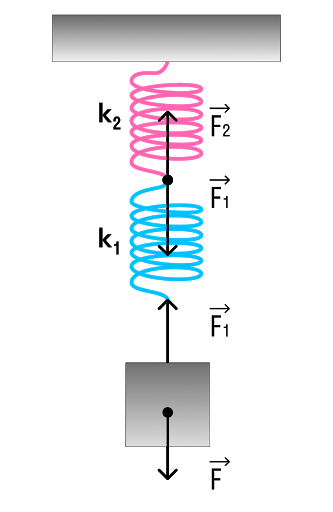
При последовательном соединении общая жесткость двух пружин

66,7 Н/м

Очень-очень важно!

Не забудь при расчете жесткости при последовательном соединении в конце перевернуть дробь

Заключение

Деформации, рассматриваемые в курсе школьной физики, оказывают влияние на процессы, происходящие в живом мире. В организмах человека, животных постоянно происходит кручение, изгиб, растяжение, сжатие. И для того чтобы осуществлять своевременную и полноценную профилактику проблем, связанных с осанкой или избыточным весом, медики используют зависимости, выявленные физиками при проведении фундаментальных исследований.

Например, прежде чем осуществлять протезирование нижних конечностей, выполняется детальный расчет максимальной нагрузки, на которую он должен быть рассчитан

Протезы подбираются для каждого человека индивидуально, так как важно учесть вес, рост и подвижность последнего. При нарушениях осанки применяют специальные коррекционные пояса, основанные на использовании деформации сдвига

Современная реабилитационная медицина не смогла бы существовать без использования физических законов и явлений, в том числе и без учета закономерностей различных видов деформаций

Современная реабилитационная медицина не смогла бы существовать без использования физических законов и явлений, в том числе и без учета закономерностей различных видов деформаций.