Модуль зубьев зубчатого колеса

Модуль — коническое колесо

К геометрии конических передач.

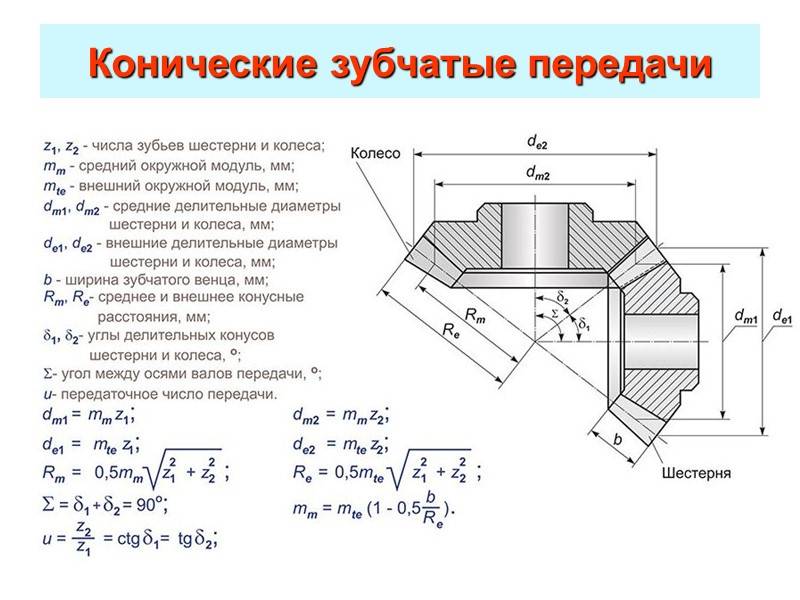
Модуль конического колеса меняется по длине зуба. За основной принимают окружной модуль на внешнем торце mte, который удобно измерять.
 

Рекомендуемые основные параметры конических передач.

Полученные значения модулей конических колес не округляют до стандартных, так как одним и тем же режущим инструментом можно нарезать колеса с различными модулями, лежащими в некотором непрерывном интервале значений. Принимать внешний окружной модуль меньше 1 5 мм нежелательно.
 

Высота зуба, шаг и модуль конического колеса переменны по длине зуба. Они максимальны на наружном дополнительном конусе и минимальны на внутреннем. По стандарту выбирают максимальный модуль т /, который определяет размеры зуба на развертке наружного дополнительного конуса.
 

Высота зуба, шаг и модуль конического колеса переменны по длине зуба. Они максимальны на наружном дополнительном конусе и минимальны на внутреннем. Для удобства измерения размеры конических колес принято определять по наружному торцу зуба, образованному наружным дополнительным конусом.
 

Метод предусматривает нарезание одной червячной фрезой определенного модуля конических колес с любым числом зубьев. Благодаря этому метод отличается универсальностью и находит применение в мелкосерийном производстве.
 

ГОСТа 9563 — 60; однако округление модуля конических колес не так существенно, как цилиндрических, так как здесь применение нестандартного модуля не вызывает необходимости в специальном зуборезном инструменте.
 

Номинальный модуль резца т0 и угол профиля ос0 могут не совпадать с параметрами тип нарезаемого колеса, так как получение необходимого угла профиля а на делительном конусе может быть обеспечено настройкой станка, а модуль конического колеса может быть нестандартным и дробным.
 

Значение модуля для конических и цилиндрических зубчатых колес одинаково. Модуль конических колес с пропорционально понижающейся высотой зуба определяется по внешнему диаметру в торцовом сечении, который принято называть окружным модулем tnt. При расчете конических колес с прямыми и криволинейными зубьями, в отличие от цилиндрических колес, полученный расчетным путем модуль можно не округлять до ближайшего стандартного значения.
 

Значение радиусов для профиля зуба при т мм.

Чертежи разрезов выполняются с соблюдением условностей изображения зубчатых колес в разрезах ( см. ГОСТ 3455 — 59, ГОСТ 3460 — 59, ГОСТ 9250 — 59), причем, если секущая плоскость проходит по зубу, то последний не штрихуется. Модуль конического колеса определяется измерением наибольшей высоты зуба ( фиг.
 

У конических колес одна и та же пара зубострогальных резцов формирует зуб по всей его длине, несмотря на то, что размеры зуба плавно уменьшаются по мере приближения к вершине конуса и в различных сечениях колеса модуль различен. Строгого соответствия номинального модуля резцов модулю нарезаемого колеса не требуется, допустимы отклонения в определенном диапазоне. Поэтому ряд модулей конических колес не регламентирован, внешний модуль может быть нестандартным и дробным.
 

Как и у цилиндрических колес, шаг и модуль плоского колеса переносятся в процессе нарезания по методу обкатывания с инструмента на начальный конус нарезаемого колеса. Для конических колес не делают различия между начальным и делительным конусами. Так как значение шага зависит от расстояния поперечного сечения колеса до вершины делительного конуса, то под шагом и модулем конического колеса подразумевают шаг pte и модуль те на делительной окружности его внешнего торца.
 

Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют – реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

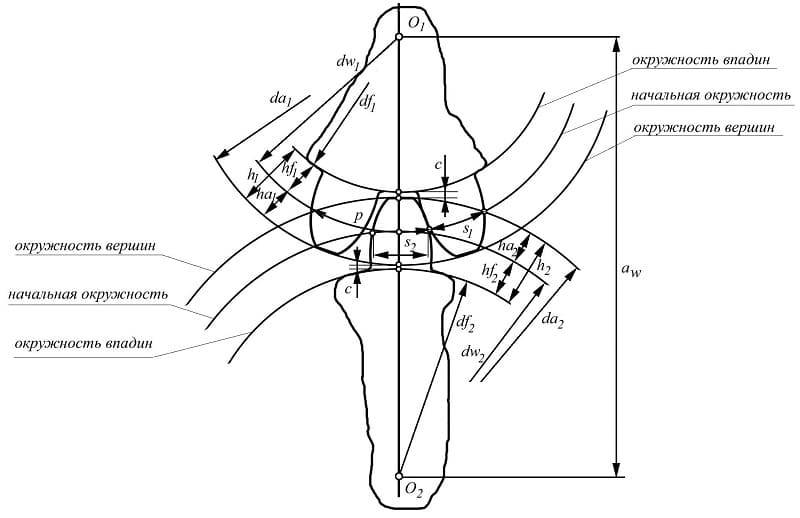
Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

ПРИЛОЖЕНИЕ 2 (рекомендуемое). ВЫБОР КОЭФФИЦИЕНТОВ СМЕЩЕНИЯ И КОЭФФИЦИЕНТОВ ИЗМЕНЕНИЯ РАСЧЕТНОЙ ТОЛЩИНЫ ЗУБА ИСХОДНОГО КОНТУРА

ПРИЛОЖЕНИЕ 2Рекомендуемое

1. В передачах с 1 шестерню рекомендуется выполнять с положительным смещением по табл.1, а колесо с равным ему по величине отрицательным смещением .

Таблица 1

Коэффициенты смещения для ортогональных конических зубчатых передач с прямыми зубьями при исходном контуре по ГОСТ 13754-81

Число зубьев шестерни	Значения коэффициента смещения при передаточном числе передачи
	1	1,12	1,25	1,4	1,6	1,8	2,0	2,5	3,15	4,0	5,0	6,3 и выше
12	—	—	—	—	—	—	—	0,50	0,53	0,56	0,57	0,58
13	—	—	—	—	—	—	0,44	0,48	0,52	0,54	0,55	0,56
14	—	—	—	0,27	0,34	0,38	0,42	0,47	0,50	0,52	0,53	0,54
15	—	—	0,18	0,25	0,31	0,36	0,40	0,45	0,48	0,50	0,51	0,52
16	—	0,10	0,17	0,24	0,30	0,35	0,38	0,43	0,46	0,48	0,49	0,50
18	0,00	0,09	0,15	0,22	0,28	0,33	0,36	0,40	0,43	0,45	0,46	0,47
20	0,00	0,08	0,14	0,20	0,26	0,30	0,34	0,37	0,40	0,42	0,43	0,44
25	0,00	0,07	0,13	0,18	0,23	0,26	0,29	0,33	0,36	0,38	0,39	0,40
30	0,00	0,06	0,11	0,15	0,19	0,22	0,25	0,28	0,31	0,33	0,34	0,35
40	0,00	0,05	0,09	0,12	0,15	0,18	0,20	0,22	0,24	0,26	0,27	0,28

Примечание. Данные таблицы могут быть использованы для неортогональных передач, если вместо и принимать соответственно и , а также для повышающих передач при 3,15, у исходного контура шестерни и соответственно уменьшенной у исходного контура колеса.Коэффициент изменения расчетной толщины зуба исходного контура положительный для шестерни и равный ему по величине, но обратный по знаку для колеса, рекомендуется вычислять по формуле

Формулой можно пользоваться для неортогональных передач, если заменить на , а также для повышающих передач при 3,15.Для ответственных тяжелонагруженных передач значения следует определять из расчета зубьев на изломную прочность.Для передач, у которых и отличается от указанных в табл.1, коэффициенты смещения принимаются с округлением в большую сторону.Для зубчатых колес, выполняемых не в соответствии со стандартным исходным контуром, коэффициенты смещения рекомендуется вычислять по формулам, приведенным в табл.2.

Таблица 2

Расчет коэффициентов смещения для ортогональных конических зубчатых колес с прямыми зубьями

Номер позиции	Расчетные зависимости
1
2
3
4
5
6
7	0,5 (2)·(4)·(6)
8
9	(8)-(7)
10	0,5 (6)
11	(3)·(10)
12	(10)++(9)
13	(11)+ -(9)
14
15
16
17
18
19
20
21
22	(12)·(20)
23	(13)·(21)
24	(22)
25	(23)
26	(22)-(23)
27	(7)-0,5 (26)
28	(26)·(27)
29	(7) (26)+(28)
30
31	(30)-(27)

Примечания:

1. Цифры в скобках соответствуют номерам позиций таблицы. определяется в результате последовательного выполнения действий по позициям 1-31. Исходные данные для расчета по табл.1 настоящего стандарта.

2. Расчетными формулами можно пользоваться и для неортогональных передач, если заменить и соответственно на и .

2. При 2,5 зубчатые колеса рекомендуется выполнять не только со смещением, устанавливаемым по п.1 настоящего приложения, но и с различной толщиной зуба исходного контура: увеличенной по сравнению с расчетной .

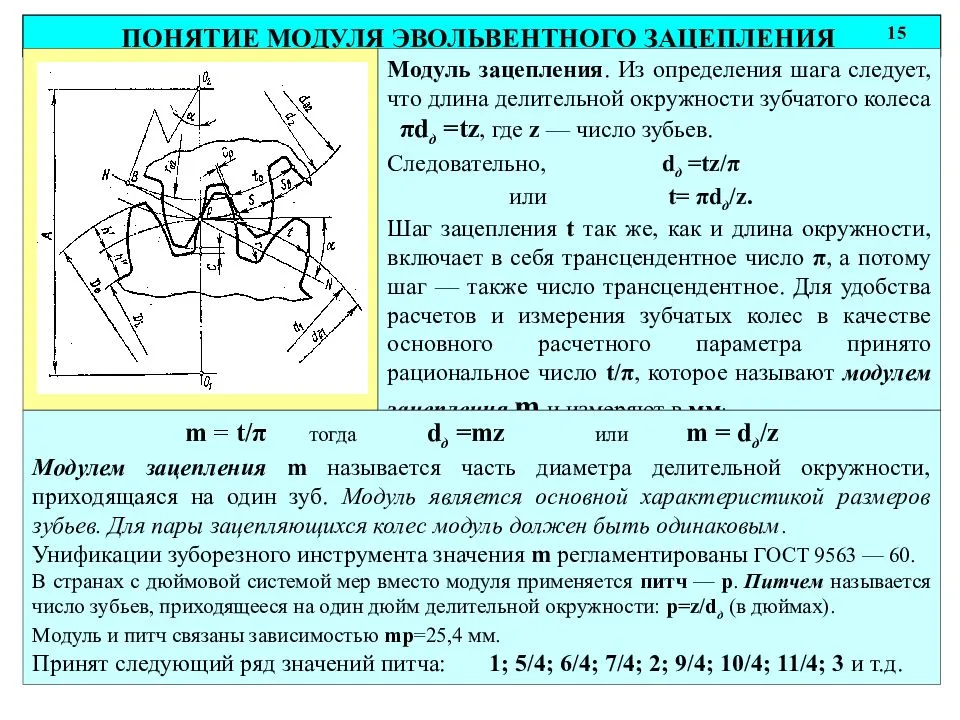
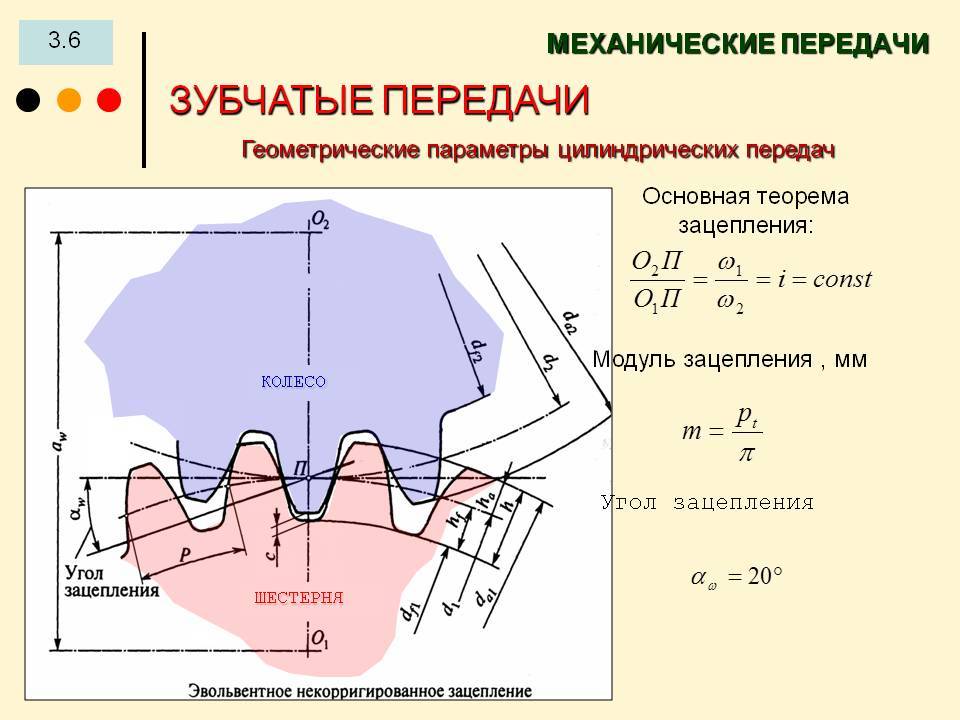
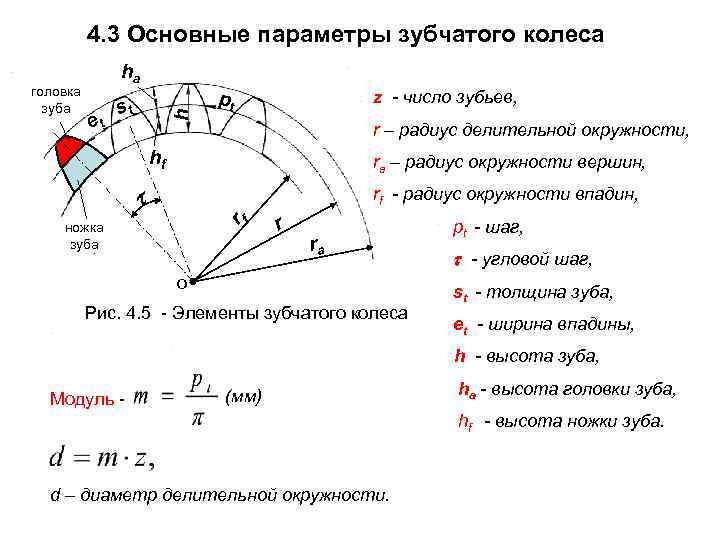
Основные определения из теории зацепления шестерен

Начальными называются воображаемые окружности, которые при зацеплении шестерен катятся без скольжения одна по другой

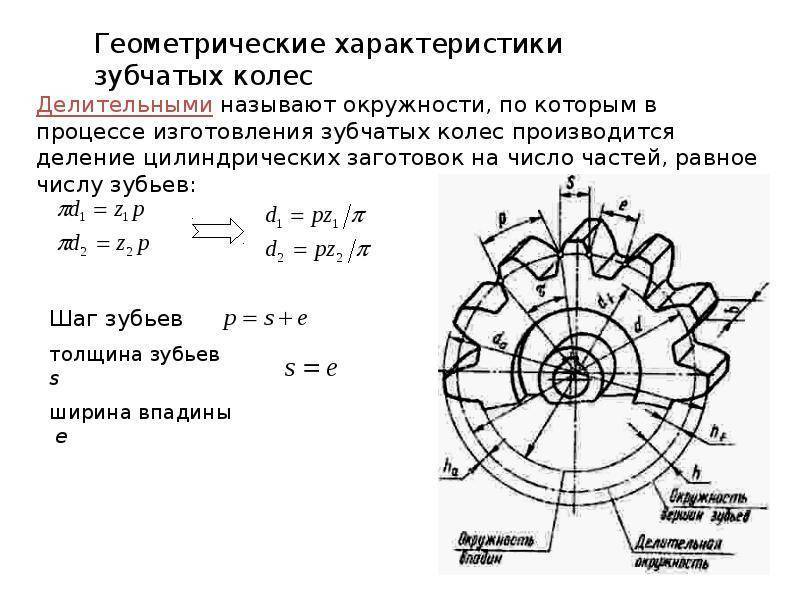
Делительными называются воображаемые окружности, по которым происходит номинальное деление зубьев. Для них справедливо уравнение: d _д = mZ Если шестерни не имеют коррекции, то начальные и делительные окружности совпадают

Окружностями выступов и впадин называются окружности, ограничивающие вершины и впадины зубьев

Основными называются окружности, по которым развертываются эвольвенты, очерчивающие профили зубьев d = d _дcosα

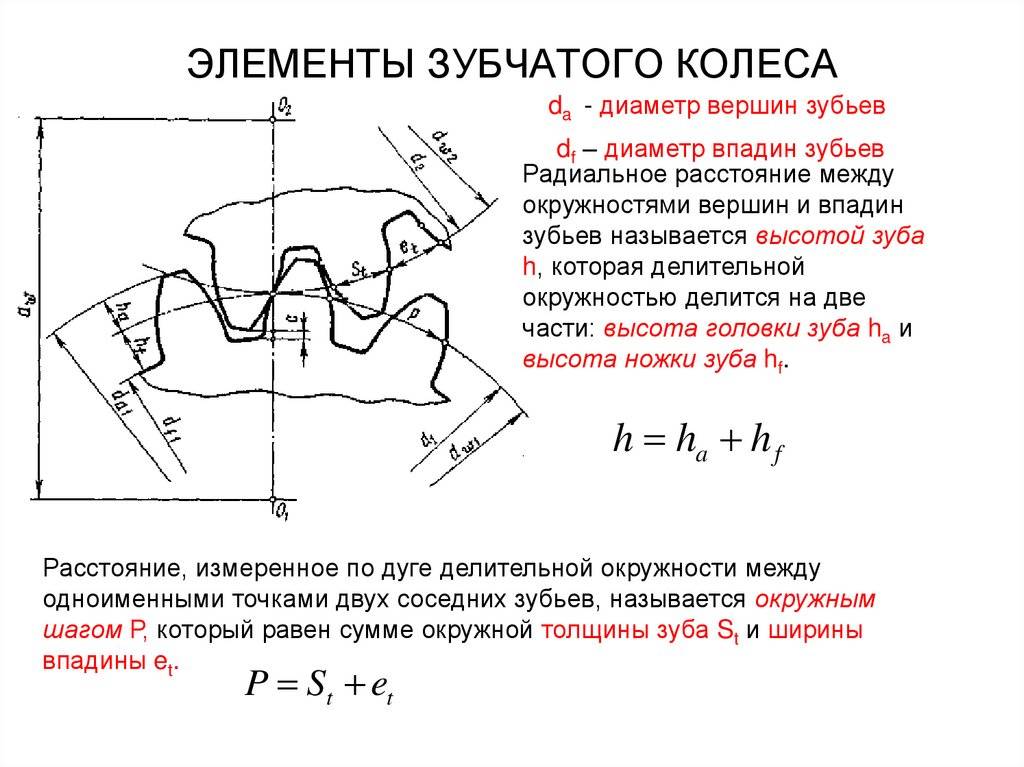
Шагом t называется расстояние по дуге делительной окружности между одноименными профилями соседних зубьев

Основным шагом t называется шаг по основной окружности

Модулем называется отношение диаметра делительной окружности к числу зубьев или шага к π

Ритчем р называется число зубьев, приходящееся на один дюйм делительной окружности

Линией зацепления ЛЗ называется геометрическое место точек контакта зубьев в зацеплении. В эвольвентном зацеплении ЛЗ — прямая, нормальная к профилю зубьев в полюсе зацепления и касательная к основным окружностям

Углом зацепления α называется угол между линией зацепления и перпендикуляром к линии центров

Углом наклона спирали зубьев косозубых шестерен β называется угол между осью зуба и образующей делительного цилиндра или конуса

Коэффициентом перекрытия ε называется отношение дуги зацепления к основному шагу

Коэффициентом коррекции ξ называется отношение величины профильного смещения к модулю

Расчет наибольшего допустимого давления зубчатых передач

Ниже приведены расчетные формулы, кото­рые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способ­ности зубчатых передач». Эти зависимости применимы для расчета нагрузки транс­миссионных зубчатых пар, работающих в стандартном режиме.

Величины и единицы измерения для расчета наибольшего допустимого давления

Необходимое сопротивление усталост­ному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высо­кого контактного давления достигается, если величина оценки сопротивления выкрашива­нию S_w равна или больше 1. В случае зубча­того зацепления с z₁< 20 следует принимать S_w ⩾ 1,2…1,5 из-за более высоких контактных напряжений в точке однопарного зацепления. Поскольку контактные давления равны по ве­личине для обоих колес, значение k_perm для зубчатого колеса 2 следует принимать такими же, как и для колеса 1 при частоте вращения n₂, пользуясь помещаемой ниже таблицей.

Формулы для расчета наибольшего допустимого давления

Содержащиеся в таблице значения коэф­фициента &_Perm применимы, когда оба колеса изготовлены из стали. Для пар зубчатых ко­лес из чугуна и стали или бронзы и стали этот коэффициент следует увеличить в 1,5 раза. В случае зубчатых пар из чугуна по чугуну или бронзы по бронзе коэффициент k_perm следует увеличить примерно в 1,8 раза. Для зубча­того зацепления лишь с одним поверхностно упрочненным колесом, коэффициент k_perm для незакаленного колеса необходимо уве­личить на 20%. Все приведенные в таблице значения этого коэффициента рассчитаны на срок службы L_h = 5000 ч. При оценке сопро­тивления выкрашиванию металла зубчатых колес S_w расчетный срок их службы может изменяться за счет коэффициента срока службы ф.

Коэффициент допустимого контактного давления k_perm в H/mm2 для срока службы L_h = 5000 ч

Прочностные характеристики материалов для изготовления зубчатых передач приве­дены в табл. «Параметры материалов зубчатых передач«.

1. При пульсирующей нагрузке для предела усталостной прочности (N_L ⩾ 3_*106). В случае знакопеременной      нагрузки следует применять коэффициент Y_L
2. В пределах усталостной прочности в течение срока службы напряжения изгиба увеличиваются на коэффици­ент Y_nt в зависимости от количества циклов нагрузки N_L.

Коэффициент срока службы ф

Коэффициент срока службы используется для корректирования приведенных в верх­ней таблице значений коэффициента допу­стимого контактного давления k_perm (рас­считанного на срок службы L_h = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.

Рекомендации по выбору расчетного срока службы зубчатых передач: при посто­янной работе с полной нагрузкой — от 40 000 до 150 000 ч; при прерывистой полной на­грузке — от 50 до 5000 ч.

Необходимая величина сопротивления разрушению зуба обеспечивается при S_F ⩾ 1 для шестерни (колесо 1). Если шестерня изготовлена из более проч­ного материала, чем зубчатое колесо 2, сле­дует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки.

Скоростной фактор f_v

Оценка действительна для А = 6 (средний уровень точности).

Пример HTML-страницы

РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ:

Пример HTML-страницы

Эскизирование детали типа «колесо зубчатое»

Последовательность выполнения эскизов зубчатого колеса:

1. Внимательно осмотреть зубчатое колесо, изучить его конструкцию, назначение, технологию изготовления.

2. Определить минимальное, но достаточное количество изображений (видов, разрезов, сечений), необходимых для полного представления о конструкции детали. Ознакомиться с правилами изображения зубчатого колеса данного вида согласно требованиям соответствующих стандартов.

3. Избрать согласно ГОСТ 2.301-68 формат чертежа, начертить на нем рамку и основную надпись.

4. Наметить тонкими сплошными линиями габаритные прямоугольники для будущих изображений с учетом равномерного использования площади листа. Провести осевые линии.

5. Обозначить тонкими сплошными линиями видимый контур детали, начиная с основных геометрических форм и сохраняя на всех изображениях проекционную связь и пропорцию элементов детали.

6. Нанести выносные и размерные линии, стрелки, проставить необходимые знаки. Провести замеры зубчатого колеса и вписать размерные числа, причем размерные числа записывать сразу после каждого измерения, не накапливая их в памяти.

7. Заполнить основную надпись и записать технические требования.

8. Внимательно проверить эскиз зубчатого колеса и исправить ошибки.

При эскизировании зубчатого колеса необходимо правильно изобразить и поставить размеры не только на элементах зубчатого зацепления, но и на конструктивных элементах соединения колеса с валом. Для этого необходимо знать не только элементы зубчатого зацепления, но и иметь представления о креплении зубчатого колеса на вале.

Зубчатые передачи используются как самостоятельные агрегаты (редукторы) или входят в другие машин как составные части.

Для передачи вращательного движения с одного вала на другой, оси которых параллельные, применяют цилиндрические передачи (рис. 5.15, а, б, в, г); если оси валов пересекаются, используют конические передачи (рис. 5.15, д, е).

Если оси валов скрещиваются (чаще под прямым углом), применяют червячные передачи (рис. 5.15, з). Для преобразования вращательного движения в поступательное и наоборот применяют реечные передачи, которые состоят из цилиндрического колеса и рейки (рис. 5.15, и). Встречаются передачи с внешним и внутренним зацеплениями (рис. 5.15, г). В первом случае вращение колес происходит в противоположных направлениях, во втором – в одном направлении.

Рисунок 5.15

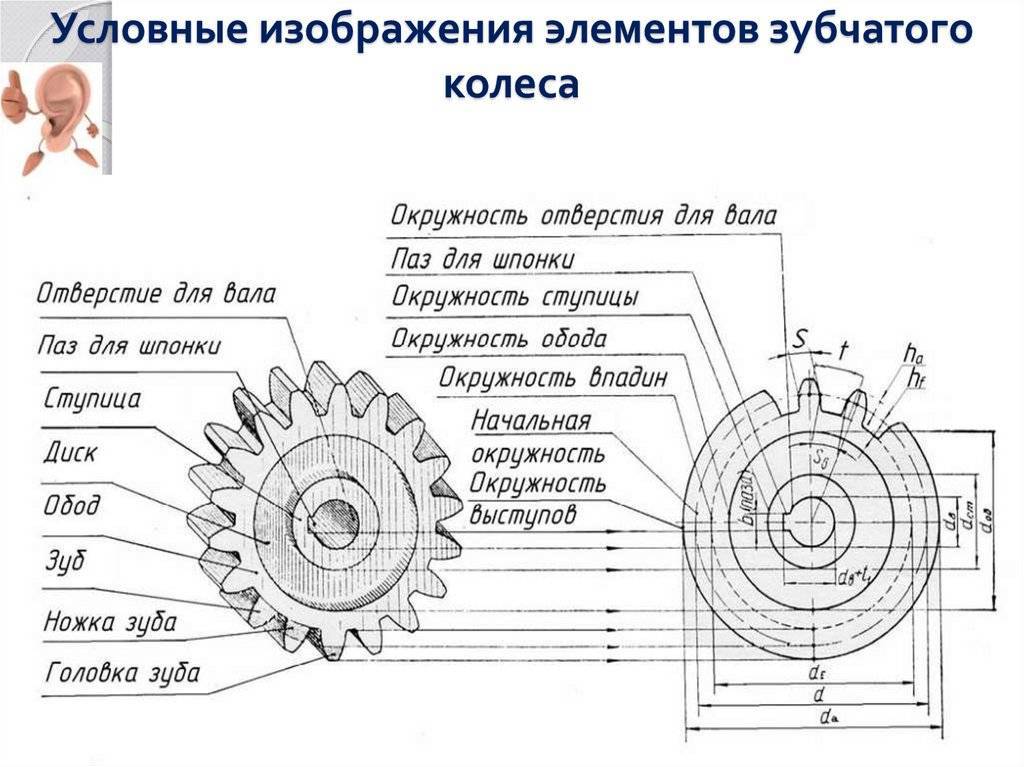
Зубчатое колесо содержит зубчатый венец и тело колеса. Зубья колеса образовывают зубчатый венец. Тело колеса ограничивается поверхностью впадин зубьев.

При изображении цилиндрических зубчатых колес приняты такие условности:

1. Поверхность вершин и ее образующую изображают сплошной основной линией, а поверхность впадин и ее образующую – сплошной тонкой линией. Делительную окружность изображают штрихпунктирною тонкой линией.

2. Зубья чертят только в осевых разрезах, изображая их не рассеченными. Если надо показать профиль зуба, то оформляют это выносными элементом или изображают его на ограниченном участке детали.

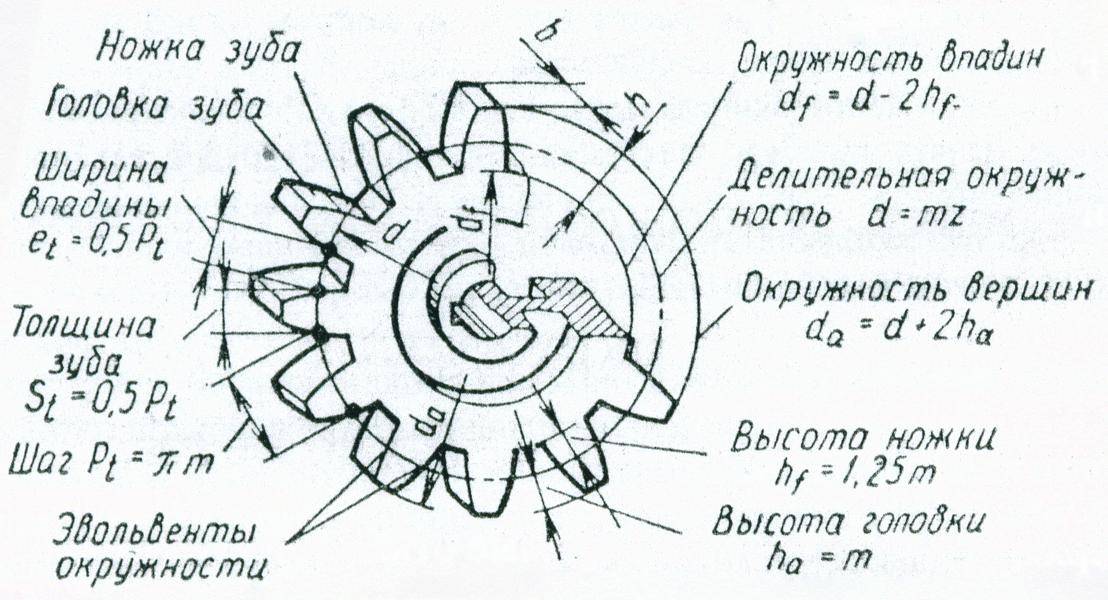
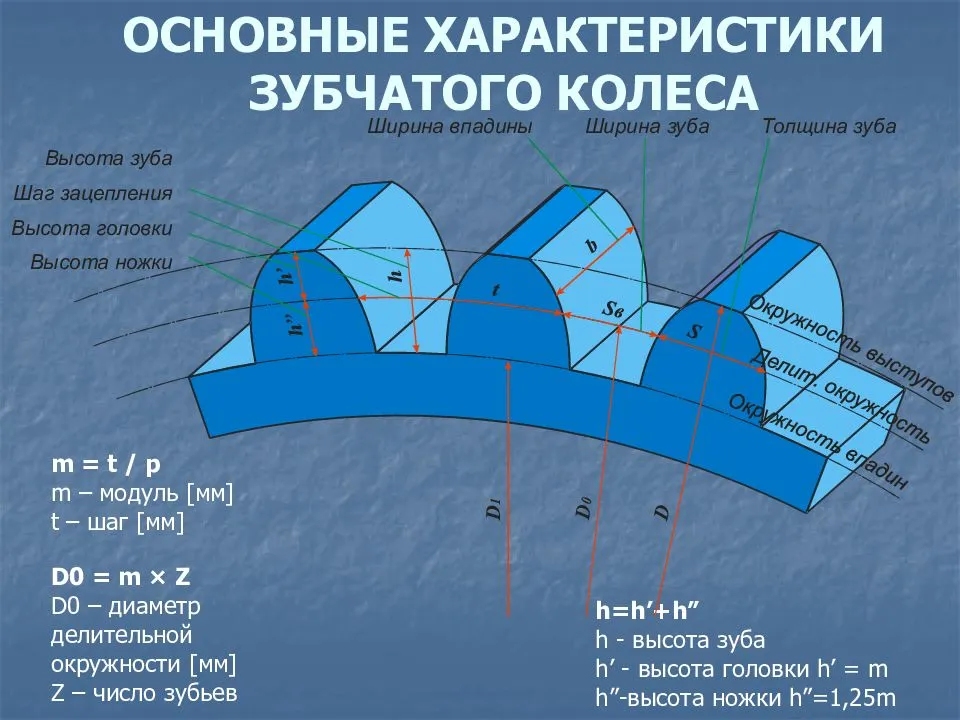
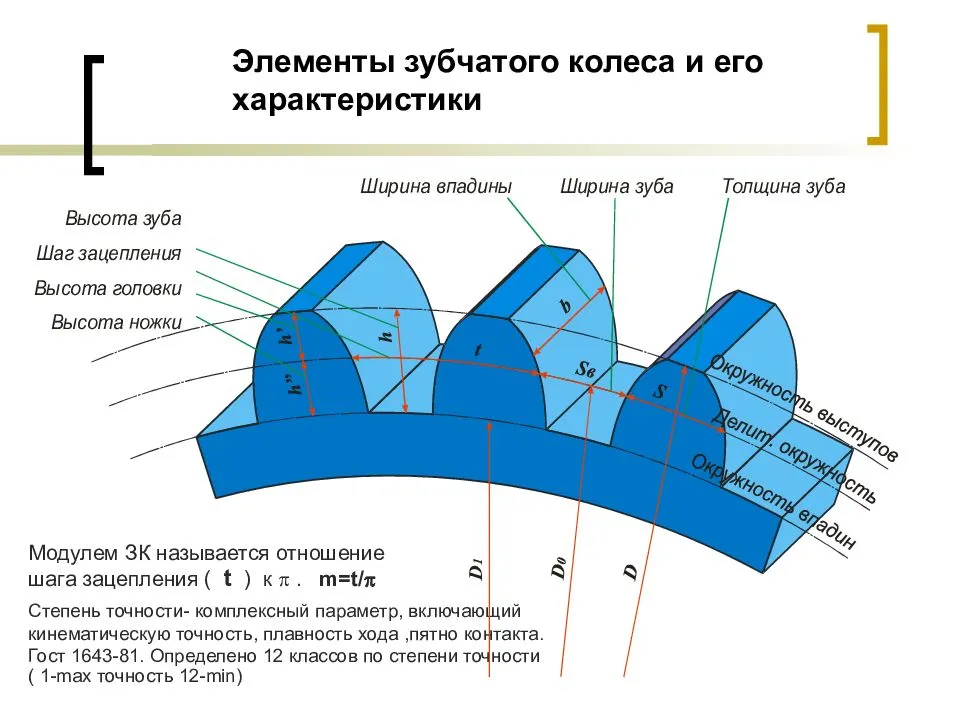
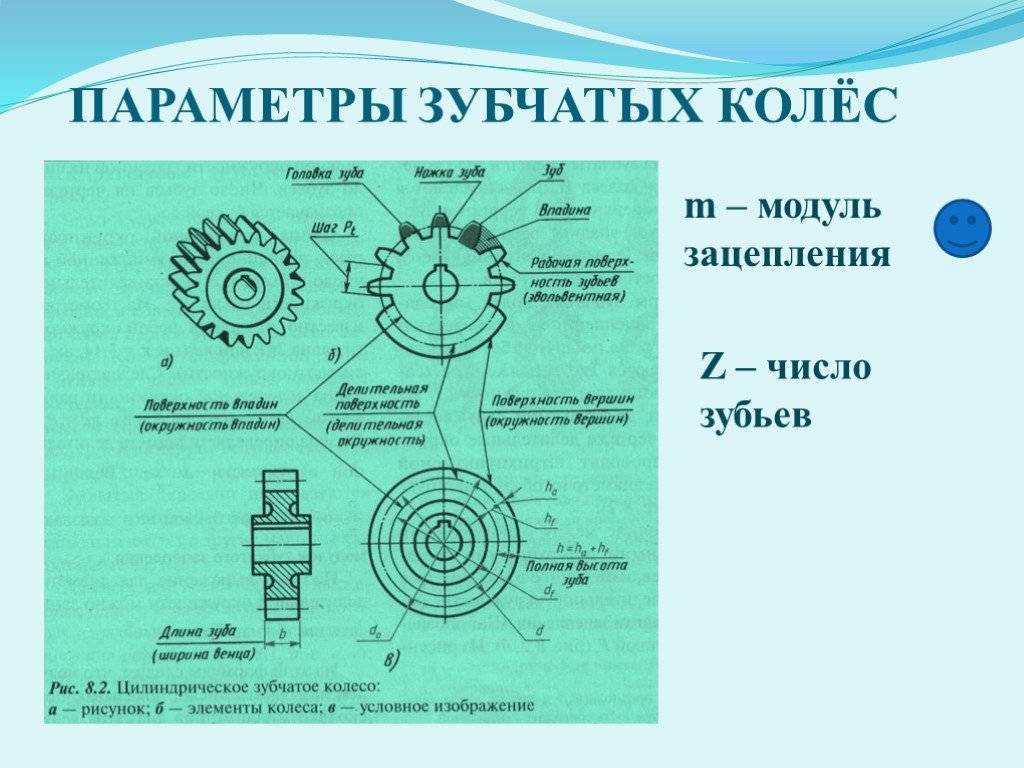
На рис. 5.16 изображены основные элементы зубчатого колеса.

Рисунок 5.16

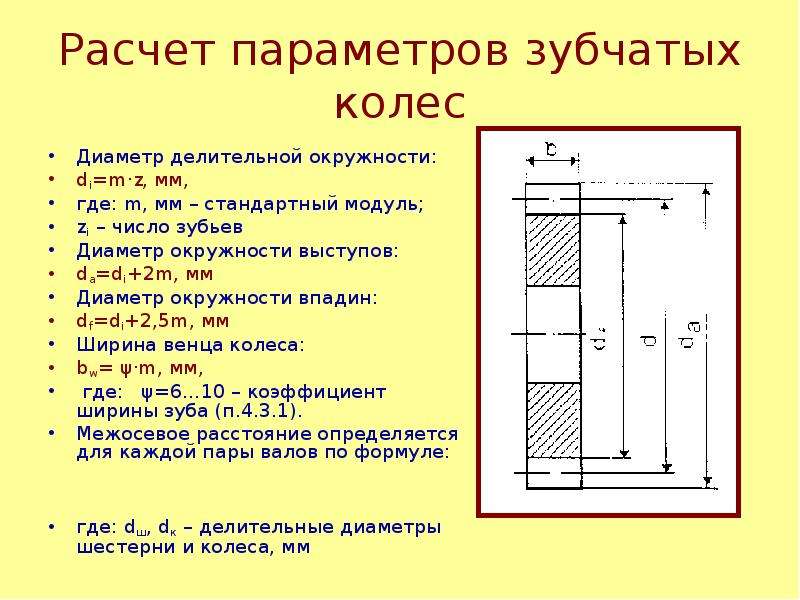
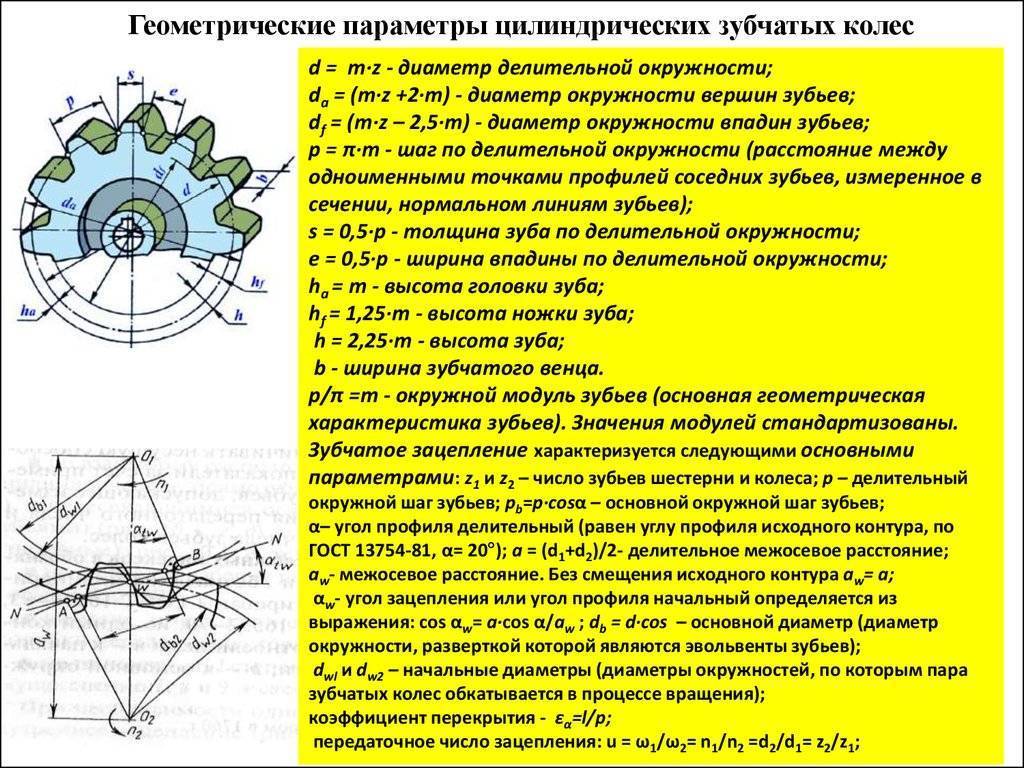
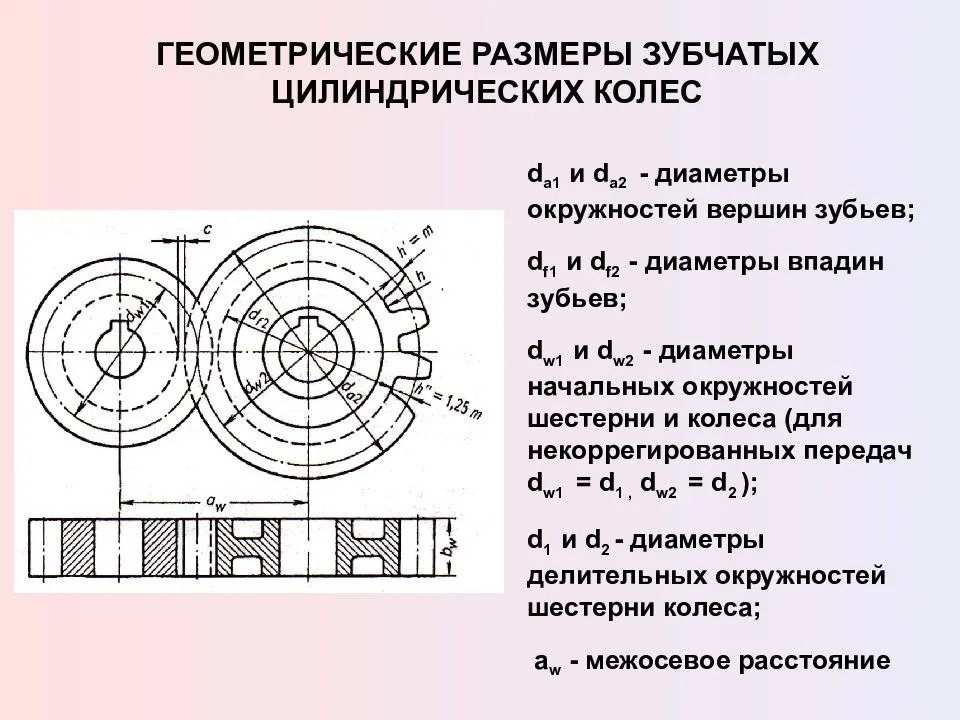
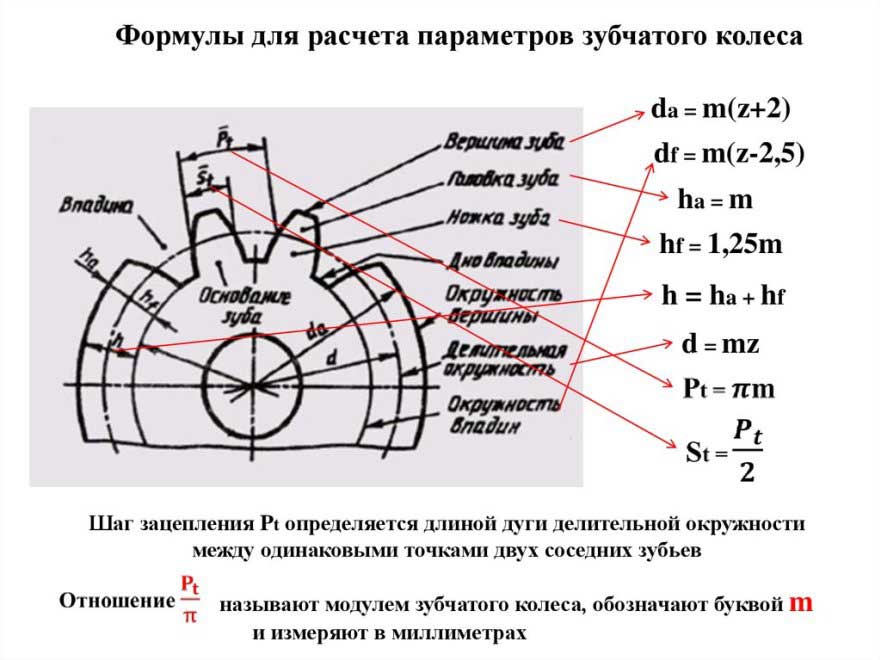
Согласно ГОСТ 16531-83 основные параметры зубчатого колеса:

1) диаметр делительной окружности d

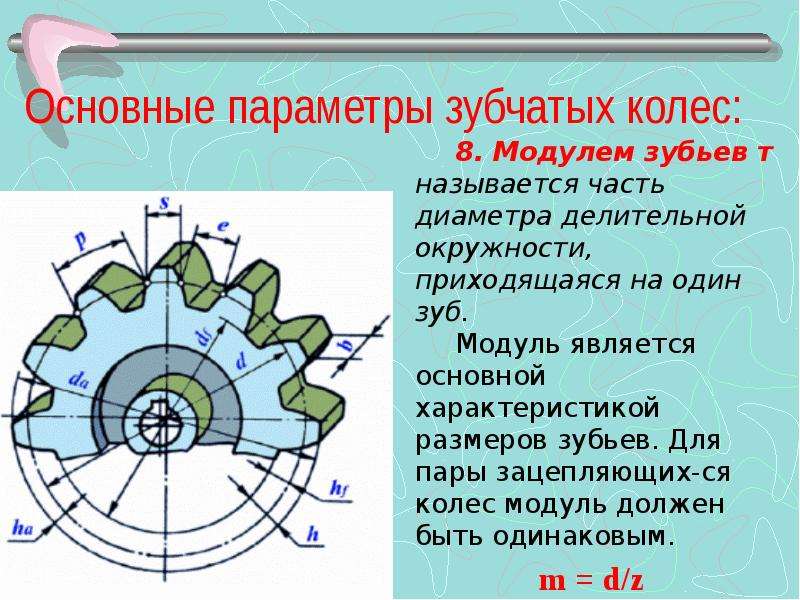
2) модуль m

– число, которое показывает, сколько миллиметров диаметра делительной окружности приходится на один зуб (количество зубьевz ):

Величины модуля стандартизированы (табл. 5.11).

Таблица 5.11 – Модули, мм ( ГОСТ 9563-60)

1-й ряд	1,25	2,5
2-й ряд	1,125	1,375	2,25	2,75	3,5	4,5	5,5

С помощью параметров, приведенных в табл. 5.12, можно рассчитать величины, которые характеризуют зацепление.

Таблица 5.12 – Параметры цилиндрического зубчатого колеса

Параметр зубчатого колеса	Обозначение	Величина, мм
Высота головки зуба	ha	ha = m
Высота ножки зуба	hf	hf = 1.25 m
Высота зуба	h	h = 2.25 m
Диаметр делительной окружности	d	d = m Z
Диаметр окружности выступов	da	da = d + 2 ha
Диаметр окружности впадин	df	df = d – 2 hf

Используя эти соотношения, можно вычислить значение модуля для реального цилиндрического колеса:

В учебных целях добытое значение необходимо округлить к ближайшему по ГОСТ 9563-60.

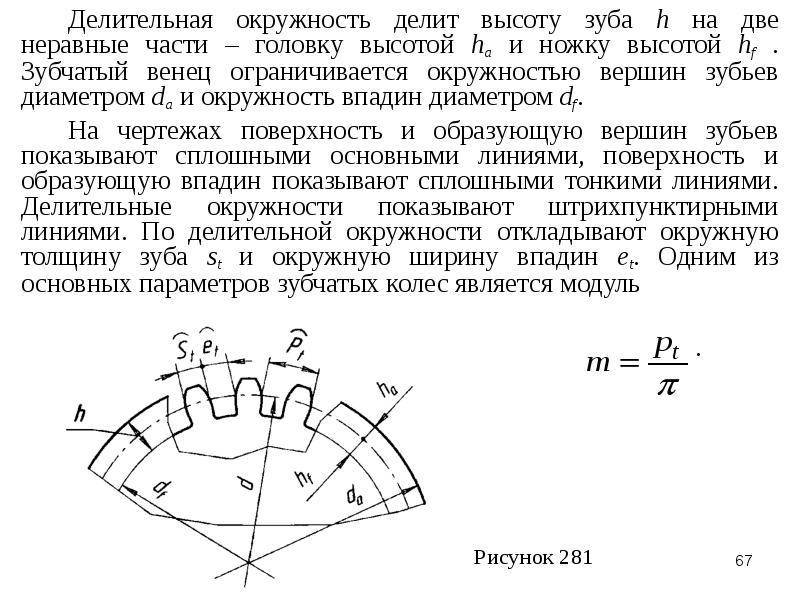
Расстояние между одноименными профильными поверхностями соседних зубьев, измеренное в миллиметрах по дуге делительной окружности, называют шагом зацепления Pt.

Из рисунка видно, что шаг равняется соотношению длины делительной окружности к числу зубьев:

Параметры зубчатых колес задают на чертежах в специальных таблицах (ГОСТ 2.403-75).

На рис. 5.17 показано расположения и размеры таблицы параметров.

Рисунок 5.17

В случае необходимости отдельные строки из нее можно опускать. Пример выполнения чертежа колеса зубчатого (для учебных целей) приведен на рис. 5.18.

Рисунок 5.18

Эффективность передач

К сожалению, в зубчатой передаче вы имеете определенные энергетические потери. Это обусловлено очевидными причинами, такими как трение, рассогласование углов давления, смазкой, зазорами (расстоянием между сцепленными зубьями двух шестерен), а также угловыми моментами и т. д. Различные типы передач, разные виды зубчатых колес, различные материалы и износ шестерен, – все это будет влиять на КПД передачи. Возможные их комбинации дадут слишком большой список, поэтому точную величину КПД передачи, которые вы используете, вы сможете найти в документации на нее.

Предположим, что вы используете два цилиндрических зубчатых колеса. Обычное КПД такой передачи примерно ~ 90%. Умножьте это число на вашу скорость выходную и момент выходной, чтобы получить истинные выходные величины передачи.

Если (из предыдущего примера):

Передаточное число = 2/3

Момент _{выходной} = Момент _{входной} * 2/3 = 1 Н∙м,

Скорость _{выходная} = Скорость _{входная} * 3/2 = 150 об/с,

то тогда:

Истинный Момент _{выходной} = 1 Н∙м * 0,9= 0,9 Н∙м,

Истинная Скорость _{выходная} = 150 об/с * 0,9 = 135 об/с.

Изготовление зубчатых колёс

Существует несколько  методов изготовления колес.

Метод обката

В настоящее время является наиболее технологичным, а поэтому и самым распространённым способом изготовления зубчатых колёс. При изготовлении зубчатых колёс могут применяться такие инструменты, как гребёнка, червячная фреза и долбяк.

Метод обката с применением гребёнки

Изготовление шестерни.
Изготовление зубчатого колеса.

Режущий инструмент, имеющий форму зубчатой рейки, называется гребёнкой. На одной стороне гребёнки по контуру её зубьев затачивается режущая кромка.

Заготовка накатываемого колеса совершает вращательное движение вокруг оси. Гребёнка совершает сложные перемещения, состоящие из поступательного движения перпендикулярно оси колеса и возвратно-поступательного движения (на анимации не показано), параллельного оси колеса для снятия стружки по всей ширине его обода. Относительное движение гребёнки и заготовки может быть и иным, например, заготовка может совершать прерывистое сложное движение обката, согласованное с движением резания гребёнки.

Заготовка и инструмент движутся на станке друг относительно друга так, как будто происходит зацепление профиля нарезаемых зубьев с исходным производящим контуром гребёнки.

Метод обката с применением червячной фрезы

Помимо гребёнки в качестве режущего инструмента применяют червячную фрезу. В этом случае между заготовкой и фрезой происходит червячное зацепление.

Метод обката с применением долбяка

Зубчатые колёса также долбят на зубодолбёжных станках с применением специальных долбяков.

Зубодолбёжный долбяк представляет собой зубчатое колесо, снабжённое режущими кромками. Поскольку срезать сразу весь слой металла обычно невозможно, обработка производится в несколько этапов.

При обработке инструмент совершает возвратно-поступательное движение относительно заготовки. После каждого двойного хода, заготовка и инструмент поворачиваются относительно своих осей на один шаг. Таким образом, инструмент и заготовка как бы «обкатываются» друг по другу. После того, как заготовка сделает полный оборот, долбяк совершает движение подачи к заготовке. Этот процесс происходит до тех пор, пока не будет удалён весь необходимый слой металла.

Литейная форма для бронзового храпового колеса (Китай, династия Хань. (206 до н. э. — 220 н. э.)).

Метод копирования (Метод деления)

Дисковой или пальцевой фрезой нарезается одна впадина зубчатого колеса. Режущая кромка инструмента имеет форму этой впадины. После нарезания одной впадины заготовка поворачивается на один угловой шаг при помощи делительного устройства, операция резания повторяется.

Метод применялся в начале XX века. Недостаток метода состоит в низкой точности: впадины изготовленного таким методом колеса сильно отличаются друг от друга.

Горячее и холодное накатывание

Процесс основан на последовательной деформации нагретого до пластического состояния слоя определенной глубины заготовки зубонакатным инструментом. При этом сочетаются индукционный нагрев поверхностного слоя заготовки на определенную глубину, пластическая деформация нагретого слоя заготовки для образования зубьев и обкатка образованных зубьев для получения заданной формы и точности.

Изготовление конических колёс

Технология изготовления конических колёс теснейшим образом связана с геометрией боковых поверхностей и профилей зубьев.

Способ копирования фасонного профиля инструмента для образования профиля на коническом колесе не может быть использован, так как размеры впадины конического колеса изменяются по мере приближения к вершине конуса. В связи с этим такие инструменты, как модульная дисковая фреза, пальцевая фреза, фасонный шлифовальный круг, можно использовать только для черновой прорезки впадин или для образования впадин колёс не выше восьмой степени точности.

Для нарезания более точных конических колёс используют способ обкатки в станочном зацеплении нарезаемой заготовки с воображаемым производящим колесом. Боковые поверхности производящего колеса образуются за счёт движения режущих кромок инструмента в процессе главного движения резания, обеспечивающего срезание припуска. Преимущественное распространение получили инструменты с прямолинейным лезвием. При прямолинейном главном движении прямолинейное лезвие образует плоскую производящую поверхность. Такая поверхность не может образовать эвольвентную коническую поверхность со сферическими эвольвентными профилями. Получаемые сопряжённые конические поверхности, отличающиеся от эвольвентных поверхностей, называют квазиэвольвентными.

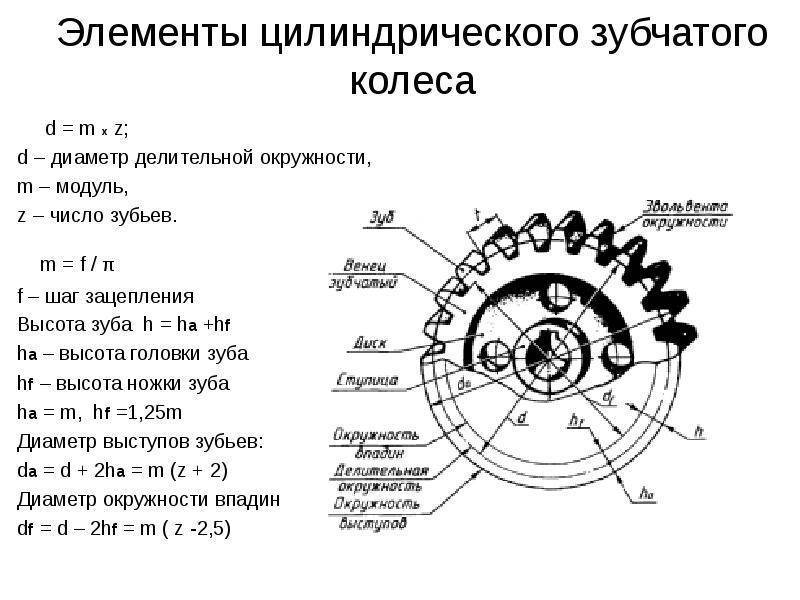
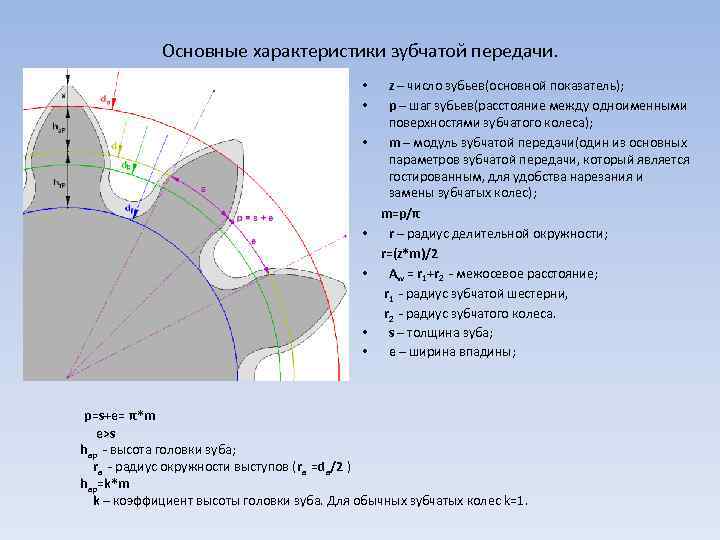
Конструкция и параметры зубчатого колеса

Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.

pmd

m = d/z= p/3,14, мм.

Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.

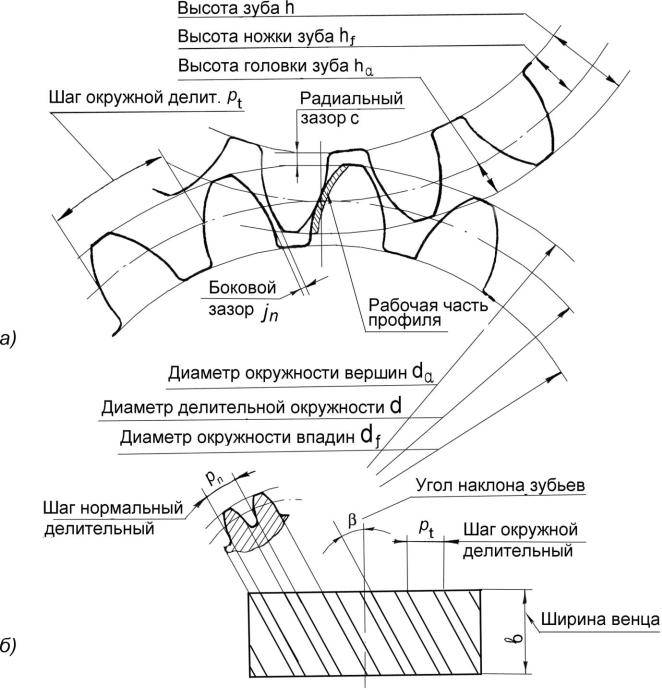
Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.

Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.