Деформация изгиба

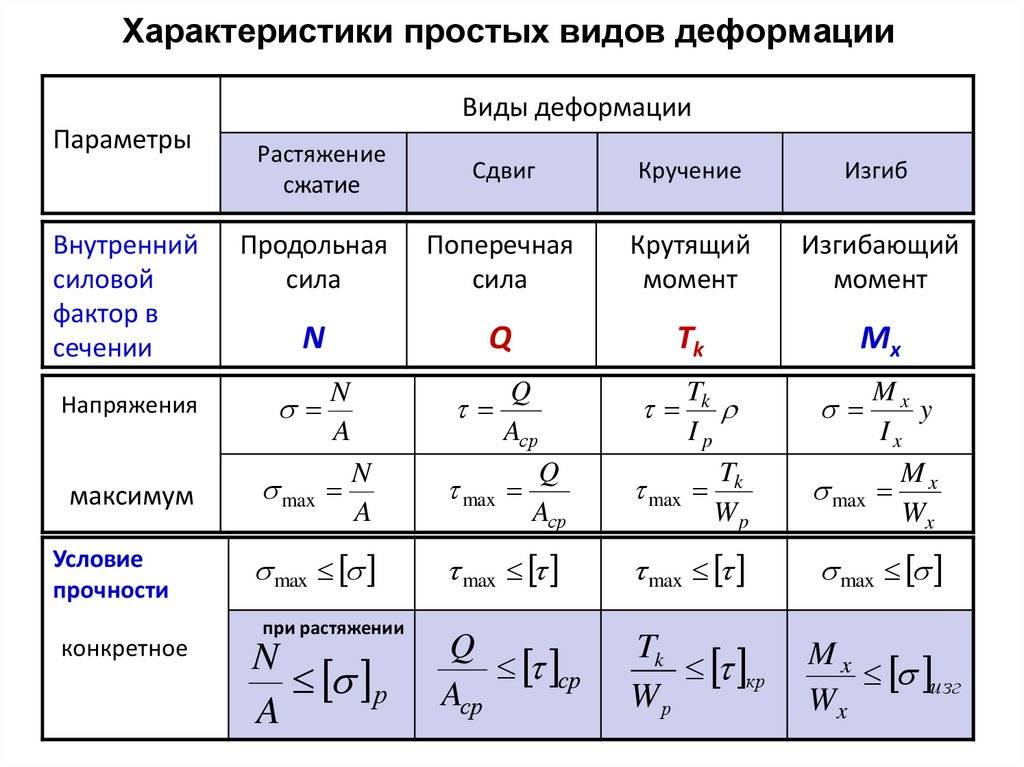
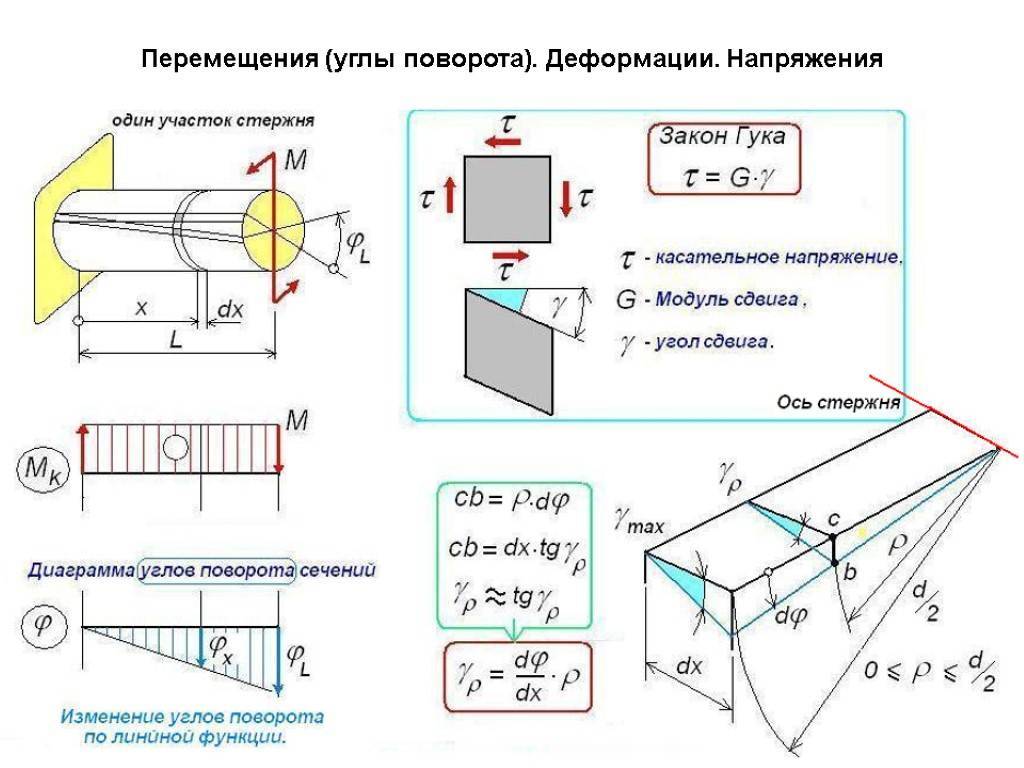
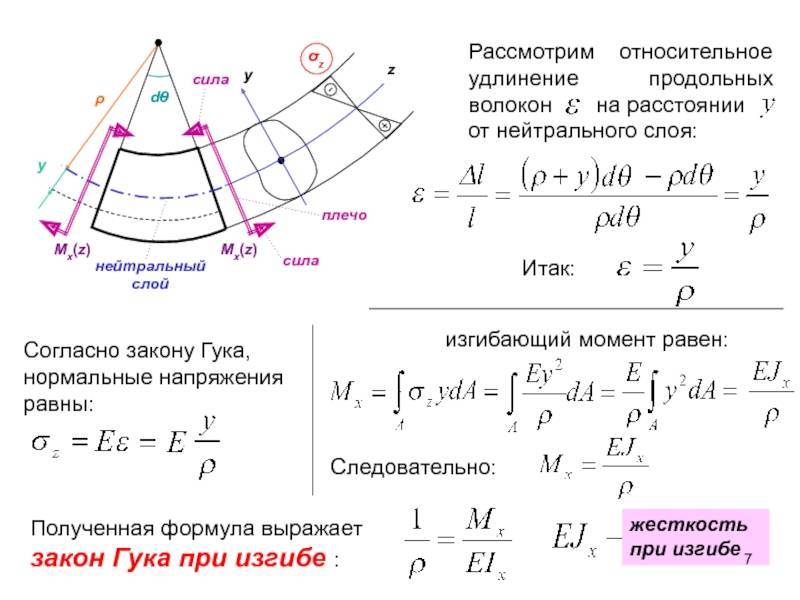
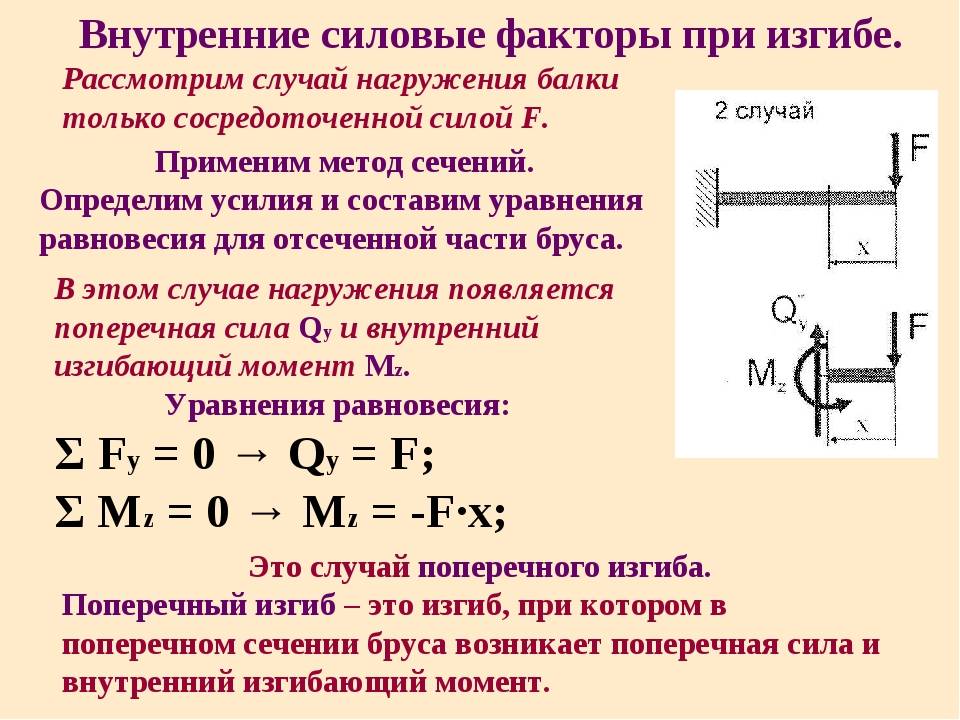
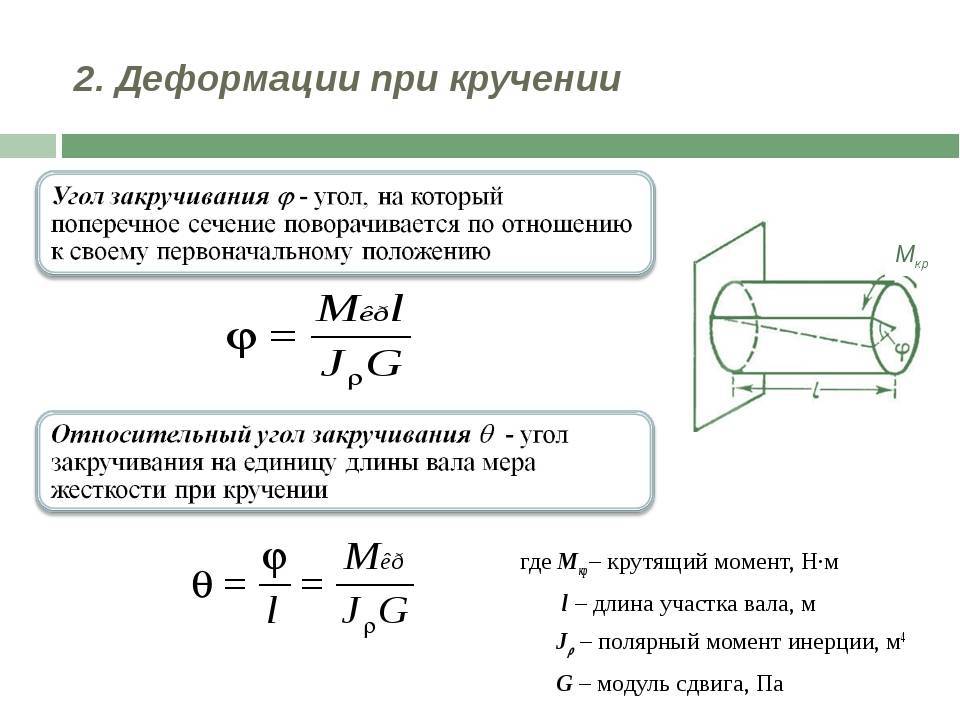
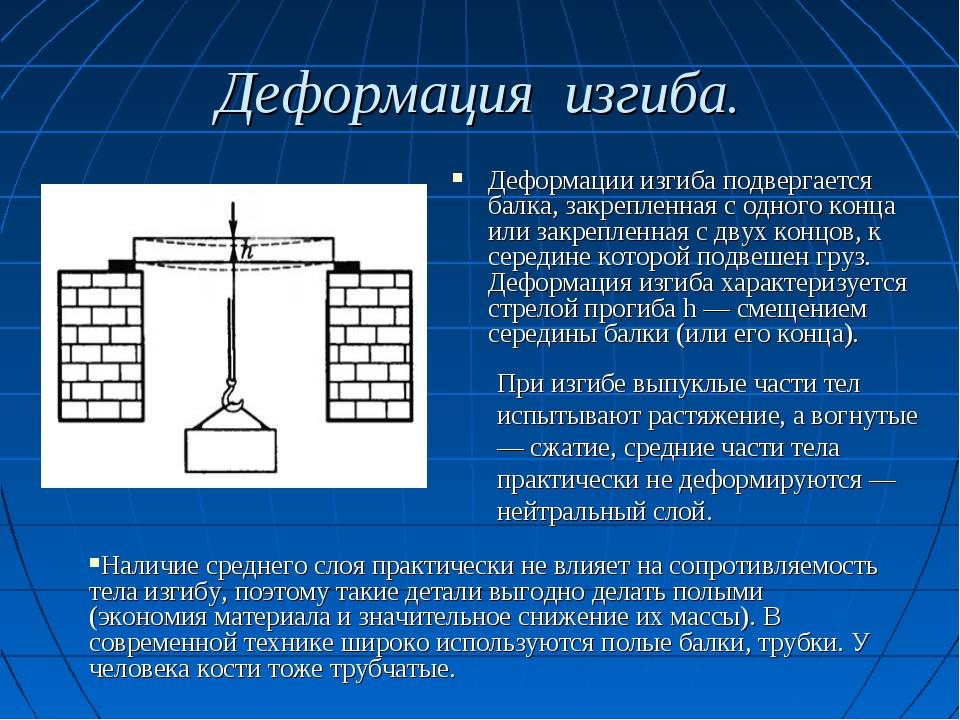
Изгибающий момент и поперечная сила

Для оценки показателей деформационных процессов, которые протекают в самых разнообразных конструкциях, используют изгибающий момент и воздействующую поперечную силу. Их рассчитывают на основании уравнений равновесия. Каждое дает возможность найти параметры каждого слоя балки при изгибе.

Во время проектирования конструкции для расчёта таких параметров берут во внимание следующие правилами:

влияние внешнего фактора, способного повернуть балку по часовой стрелке относительно проведенного сечения; образовывается изгибающий момент, который может привести к сжатию любого из волокон балки (в уравнении его берут во внимание со знаком плюс);

Полученные результаты дают возможность построить графическое изображение распределения сил и факторов на самых разных уровнях. Такие изображения называют эпюрами. При их помощи формируют крепость создаваемой конструкции.

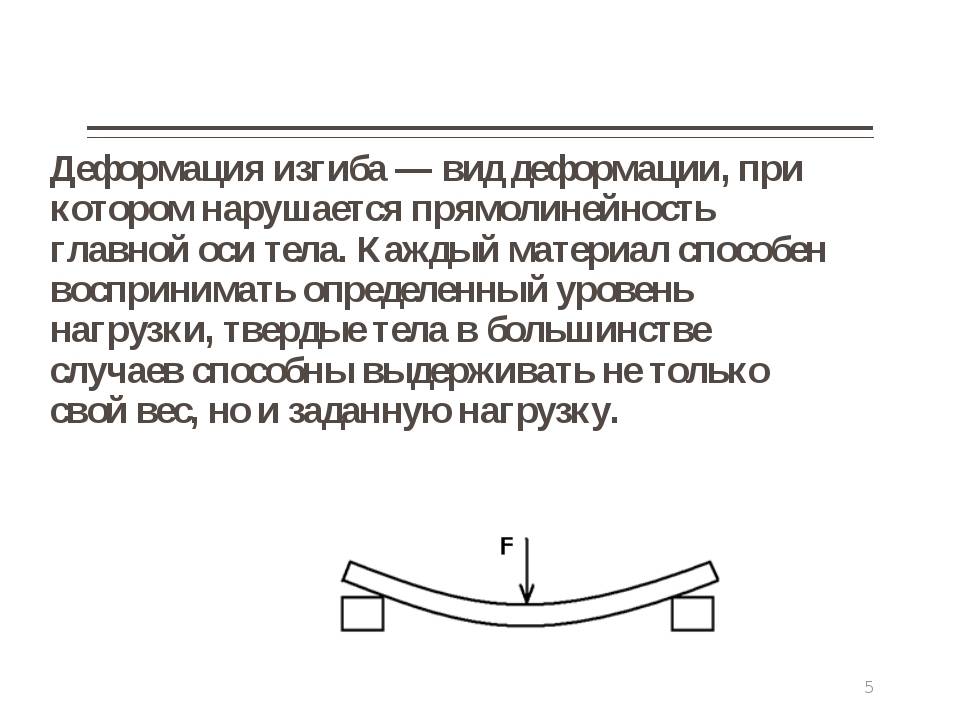
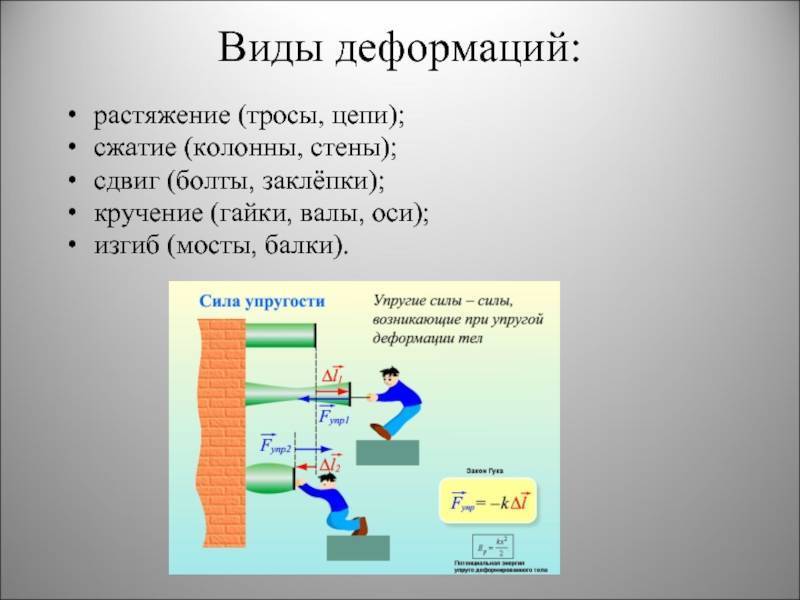
Виды деформации

Различают деформации нескольких видов. На изображении показаны некоторые из них.

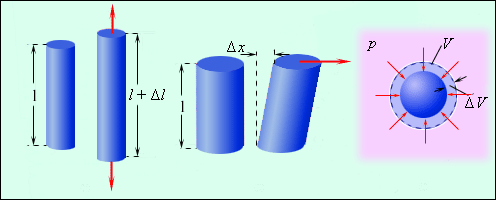
Рисунок 3.7.1. Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия.

Первый вид – растяжение или сжатие – является наиболее простым видом деформации. В таком случае изменения, происходящие с телом, можно описать при помощи абсолютного удлинения Δl, которое происходит под действием сил, обозначаемых F→. Взаимосвязь, существующая между силами и удлинением, обусловлена геометрическими размерами тела (в первую очередь толщиной и длиной), а также механическими свойствами вещества.

Определение 2

Если мы разделим величину абсолютного удлинения на первоначальную длину твердого тела, мы получим величину его относительного удлинения (относительной деформации).

Обозначим этот показатель ε и запишем следующую формулу:

ε=∆ll.

Определение 3

Относительная деформация тела растет при его растяжении и соответственно уменьшается при сжатии.

Если учесть, в каком именно направлении внешняя сила действует на тело, то мы можем записать, что F будет больше нуля при растяжении и меньше нуля при сжатии.

Прочность на изгиб цилиндра

Рассмотрим балку с простой опорой, у которой две равные нагрузки W / 2 действуют на расстоянии L / 3 от обоих концов.

Значение реакции в точках A и B можно рассчитать, применяя условия равновесия

Для вертикального равновесия

Принимая момент около A, момент по часовой стрелке положительный, а момент против часовой стрелки принимается как отрицательный.

Положив значение R_B в получаем

В соответствии с соглашением о знаках для ЮФО и ПРО

Сила сдвига в точке A

Сила сдвига при C

Сила сдвига в точке B

Для диаграммы изгибающего момента, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке воспринимается как положительный. Момент против часовой стрелки принимается как Negative.

Изгибающий момент при A = M_A = 0

Изгибающий момент при C = [Вт / 2] * [L / 3] …………………………

Изгибающий момент при C =

Изгибающий момент при D =

Изгибающий момент при B = 0

Пусть d = диаметр цилиндрической балки, согласно уравнению Эйлера-Бернулли.

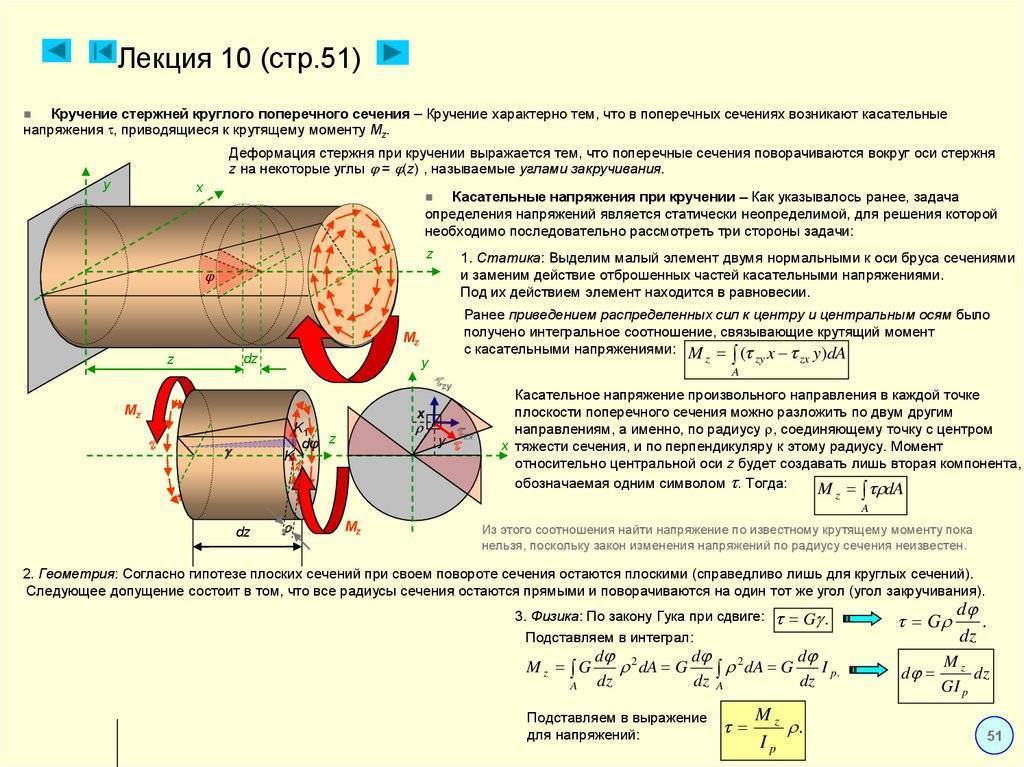
Расчёты на крепость при сдвиге

Оценка характеристик прочности изделий выполняется для определения наступления трёх факторов деформации:

1. Смещение некоторых слоёв (возникновения угла деформации).
2. Смятие крепежных элементов.
3. Сдвиг.
4. Разрыв.

Расчёт на крепость нужен для определения условий наступления любого из видов. В работе для более наглядной оценки параметров прочности и стойкости к деформированию решают существующие аналитические выражения и изображают эпюры отражающие направления влияния разных видов стрессов.

Получение численных параметров возможно благодаря использованию разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений изготавливается на основе принятых гипотез.

Расчёт возможных стрессов изготавливается на основании первой, третьей и четвёртой гипотезы прочности. Любая из гипотез принимается для различных материалов, которые обладают собственными физико-механическими свойствами.

Крепость быть на каждом из этапов разработки определенной детали. В первую очередь вычисляют величины возможных стрессов и угол отклонения на предварительном (проверочном) шаге. Это дает возможность определить их уровни, величины и направление приложенных сил. После чего приступают к проектированию. На данном шаге выполняется подбор материала детали и элементов крепежа с учитыванием достаточной прочности любого элемента конструкции. На конечном шаге ещё один раз проверяют возможные нормы нагрузки и способность готовой детали держать допустимую и дополнительную нагрузку, другими словами формируют прочностный запас.

Наиболее показательными являются расчёты для чистого сдвига. В данном случае при расчёте рассматривают следующие моменты выполнения задачи:

• Статический (составляется уравнение равновесия). В данном случае применяется предположение о равномерности распределения касательных стрессов. Впрочем в определенных случаях они делятся не одинаково, что затрудняет решение установленной задачи. Он дает возможность установить связь возникших стрессов с действующими внешними силами. Это выполняться благодаря получению семейства решений дифференциальных уравнений равновесия для всего объёма детали.
• Геометрический (деформационный). Позволяет отобразить связь между отдельными маленькими участками исследуемой детали.
• Математический. Дает возможность подобрать метод решения составленной системы уравнений. Провести математическое моделирование протекающих процессов.
• Физический. Устанавливает связь между физическими процессами при деформации с учитыванием физических параметров материала и возникшими напряжениями (механическими качествами).

На математическом и физическом шаге рассмотрения установленной задачи используются следующие главные расчетные выражения и допущения:

• закон Гука для деформации смещения;
• гипотезы прочности (с учитыванием физических и механических параметров материала который для него выбран);
• выбор системы равноценных стрессов;
• упрощения при изображении эпюр, отображающих направления действующих сил и возникших стрессов;
• принятие ключевых положений для случая чистого сдвига.

В первом варианте происходит пластическая дефармация детали, когда интенсивность возникших стрессов превосходит предел текучести материала который для него выбран. Размер подобной деформации зависят от характера и интенсивности действия внешних сил, прочностных показателей материала, изменения режима температур.

При интенсивности влияния, превышающем крепость материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (к примеру, крепежных изделий, заклёпок, втулок).

Разработанные методы расчёта прочности дают возможность проектировать и делать детали с заданием, превышающим этот предел. Это дает возможность значительно повысить прочность и долговечность всей конструкции. Сейчас разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с использованием созданных программных средств, которые дают возможность получить числовые характеристики прочности и выстроить графические изображения эпюр в формате 3D графики.

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.

Тестирование сварных швов и расчет деформаций

С целью определения прочности и надежности шва, и выявления возникших дефектов проводится тестирование сварных соединений. Такой контроль позволяет своевременно обнаружить браки и оперативно их устранить.

Для выявления изъянов используют следующие типы контроля:

• разрушающий. Позволяет исследовать физические качества сварного шва, активно применятся на производственных предприятиях;
• неразрушающий. Проводится посредством внешнего осмотра, капиллярного метода, магнитной или ультразвуковой дефектоскопии, контролем на проницаемость и другими способами.

При производстве конструкций с применением сварки одним из важных нюансов является точное определение возможных деформаций и напряжений. Их наличие приводит к отклонениям от первоначальных размеров и форм изделий, понижает прочность конструкций и ухудшает эксплуатационные качества.

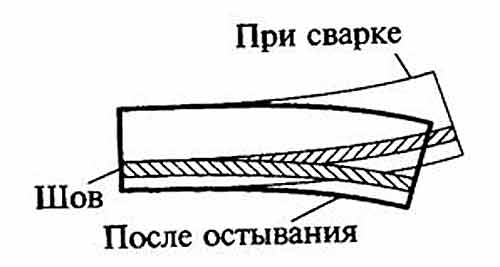
Расчет сварочных напряжений и деформаций позволяет проанализировать разные варианты проведения сварочных операций и спланировать их последовательность так, чтобы в процессе работ конструкция подвергалась минимальным напряжениям и образованию дефектов.

Билеты экзамена для проверки знаний специалистов сварочного производства 1 уровень

ВОПРОС 1. Что такое сварка плавящимся электродом?

1. Дуга горит между свариваемым изделием и плавящимся электродом или электродной проволокой.

2. Сварочная ванна защищается газом и шлаком, которые образовались в процессе плавления основного и сварочного материалов.

3. Электрод плавится за счет тепла дуги или газового пламени.

ВОПРОС 2. Какой буквой русского алфавита обозначают вольфрам и ванадий в маркировке стали?

1. Вольфрам — Г, ванадий — В.

2. Вольфрам — В, ванадий — Ф.

3. Вольфрам — К, ванадий — Б.

ВОПРОС 3. Электроды каких марок имеют рутиловое покрытие?

1. УОНИИ 13/45, СМ-11.

2. АНО-3, АНО-6, МР-3.

ВОПРОС 4. Чему равно общее напряжение нескольких одинаковых источников ЭДС, соединенных последовательно?

1. Напряжению одного из соединенных источников ЭДС.

2. Частному от деления произведений напряжений соединенных источников ЭДС на сумму их напряжений.

3. Алгебраической сумме напряжений источников ЭДС.

ВОПРОС 5. Какой частоты переменного тока, вырабатывают электростанции в России?

1. Переменный ток с частотой 100 Гц.

2. Переменный ток с частотой 60 Гц.

3. Переменный ток с частотой 50 Гц.

ВОПРОС 6. Укажите величину зазора между свариваемыми кромками элементов толщиной до 5 мм по ГОСТ 5264-80?

ВОПРОС 7. Для какой группы сталей применяют при сварке электроды типов Э38, Э42, Э42А, Э46, Э46А?

1. Для сварки теплоустойчивых низколегированных сталей.

2. Для сварки углеродистых конструкционных сталей сталей.

3. Для сварки низколегированных конструкционных сталей.

ВОПРОС 8. Что обозначает в маркировке электродов буква «Э» и цифры, следующие за ней?

1. Марку электрода и номер разработки.

2. Завод-изготовитель и номер покрытия.

3. Тип электрода и гарантируемый предел прочности наплавленного ими металла в кгс/мм2.

ВОПРОС 9. Влияет ли род и полярность тока на величину проплавления при РДС?

1. Влияет незначительно.

3. Влияет существенно.

ВОПРОС 10. Как влияет длина дуги на ширину шва?

2. С увеличением длины дуги ширина шва уменьшается.

3. С увеличение длины дуги ширина шва увеличивается.

ВОПРОС 11. В каких условиях рекомендуется хранить электроды?

1. В сухом отапливаемом помещении при температуре не ниже +15 и влажности воздуха не более 50 %.

2. В складском помещении при температуре выше 00С.

3. В ящиках, в упакованном виде.

ВОПРОС 12. Какие дефекты могут быть в сварном шве, если притупление кромок превышает рекомендуемую величину?

1. Возможно появление непровара корня шва.

2. Возможно появление холодных трещин.

3. Возможно появление пористости.

ВОПРОС 13. С какой целью источники питания сварочной дуги для ручной дуговой сварки имеют напряжение холостого хода выше, чем напряжение на дуге при сварке?

1. Для увеличения глубины проплавления в начале шва.

2. Для улучшения возбуждения дуги.

3. Для уменьшения разбрызгивания металла.

ВОПРОС 14. Какие углеродистые и низколегированные стали необходимо подогревать при сварке?

1. С эквивалентным содержанием углерода более 0,5 %.

2. С содержанием серы и фосфора более 0,05 % каждого.

3. С содержанием кремния и марганца до 0,5…1,5 % каждого.

ВОПРОС 15. Какие способы резки рекомендуется применять для подготовки деталей из аустенитных сталей?

2. Кислородно-флюсовая, плазменно-дуговая, механическая.

ВОПРОС 16. Что входит в понятие металлургической свариваемости металлов?

1. Влияние на свариваемость химического состава металла и отсутствие дефектов в результате химического взаимодействия элементов в сварочной ванне и кристаллизующемся металле шва.

2. Влияние на свариваемость способа сварки и возможность появления дефектов в результате воздействия термического цикла на сварочную ванну и кристаллизующейся металл шва.

3. Влияние на свариваемость объема сварочной ванны и кристаллизующегося металла шва.

ВОПРОС 17. Какие сварочные деформации называют остаточными?

1. Деформации, появляющиеся во время сварки.

2. Деформации, появляющиеся по окончании сварки.

3. Деформации, образующиеся под действием эксплуатационных нагрузок.

ВОПРОС 18. Допускаются ли трещины в сварных швах при сварке низколегированных сталей?

1. Допускается, если их длина не превышает толщины металла шва.

2. Допускается, если концы трещины после сварки заварить газовой сваркой.

3. Не допускаются.

ВОПРОС 19. Какой род тока более опасен при поражении человека электрическими токами при напряжении 220В?

1. Переменный ток 50 Гц.

2. Постоянный ток.

3. Ток высокой частоты.

ВОПРОС 20. Какими индивидуальными средствами должен обеспечиваться сварщик при выполнении потолочной сварки?

1. Поясом безопасности.

2. Беретом и рукавицами.

3. Нарукавниками, шлемом и пелеринами.

Для перехода на следующую страницу, воспользуйтесь постраничной навигацией ниже

Страницы: 1 2 3 4 5 6 7 8 9 10

Деформации на примере организма человека

Тело человека подвергается серьезным механическим нагрузкам от собственных усилий и веса, появляющихся по мере физической деятельности. Вообще, деформация (сдвиг) характерна для человеческого организма:

• Сжатие испытывает позвоночник, покровы ступней, нижние конечности.
• Растяжению подвергаются связки, верхние конечности, мышцы, сухожилья.
• Изгиб характерен для конечностей, костей таза, позвонков.
• Кручениям подвергается во время поворота шея, при вращении ее испытывают кисти рук.

Но при превышении показателей предельного напряжения, возможен разрыв, например костей плеча, бедра. В связках же ткани соединяются настолько эластично, что допускается растягивание их в два раза. Кстати, деформация сдвига объясняет всю опасность передвижения женщин на высоких каблуках. Вес тела будет переноситься на пальцы, что приведет к повышению нагрузки на кости в два раза.

По результатам медицинских осмотров, проводимых в школах, из десяти детей лишь одного можно считать здоровым. Как деформации связаны с детским здоровьем? Сдвиг, кручение, сжатие – основные причины нарушения осанки у детей и подростков.

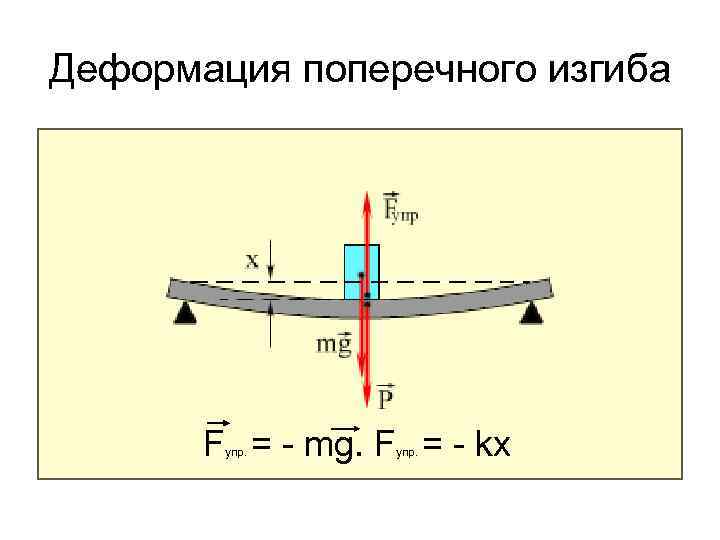
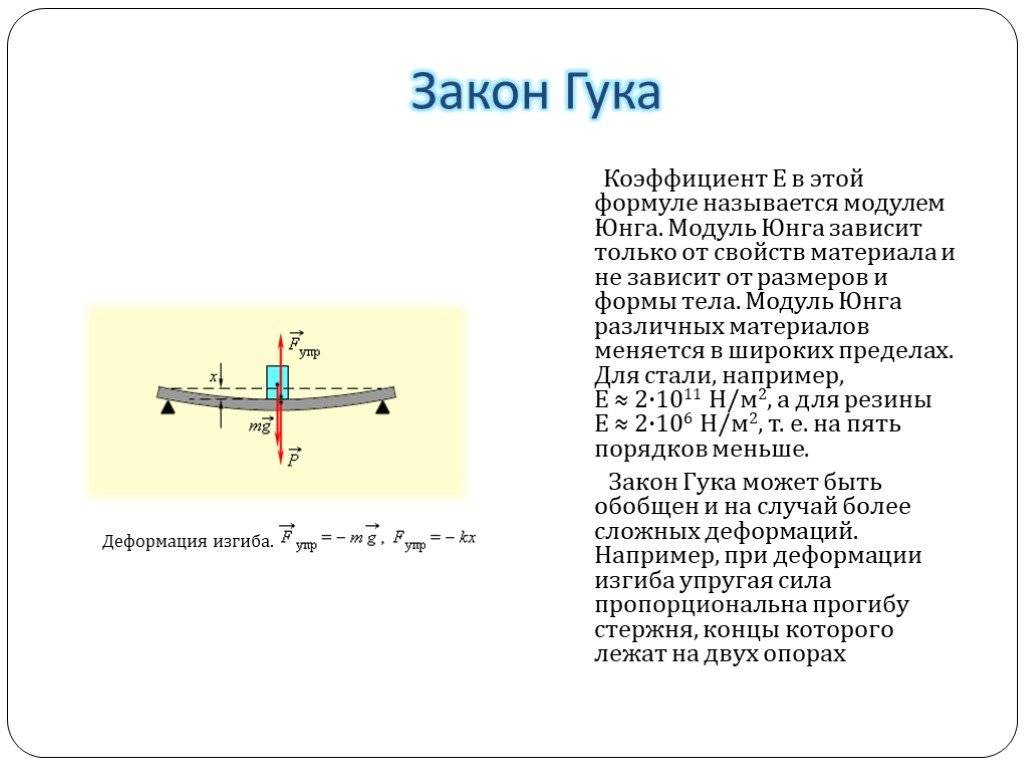
Закон Гука

Основной закон, рассматриваемый при деформации тела. Согласно ему, деформация, возникающая в теле, прямо пропорциональна воздействующей силе. Единственная оговорка заключается в том, что он применим только при малых значениях деформации, поскольку при больших значениях и превышении предела пропорциональности эта связь становится нелинейной. В простейшем случае (для тонкого растяжимого бруска) закон Гука имеет следующий вид:

Ф=к*Л,

где Ф – это приложенная сила; к – коэффициент упругости; Л – это изменение длины бруса.

Если с двумя величинами всё понятно, то коэффициент (к) зависит от нескольких факторов, таких как материал изделия и его размеры. Его значение также можно вычислить по следующей формуле:

к=(Е*С)/Л,

где Е – это модуль Юнга; С – площадь поперечного сечения; Л – длина бруса.

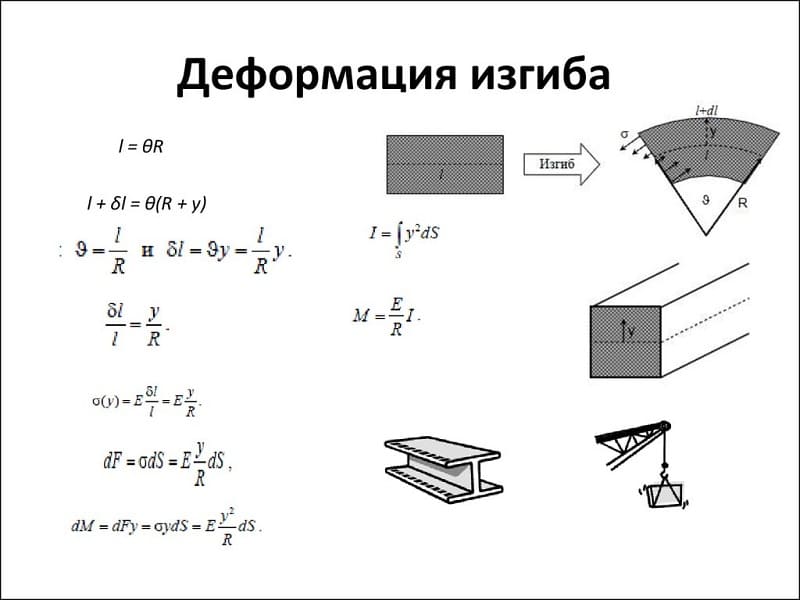
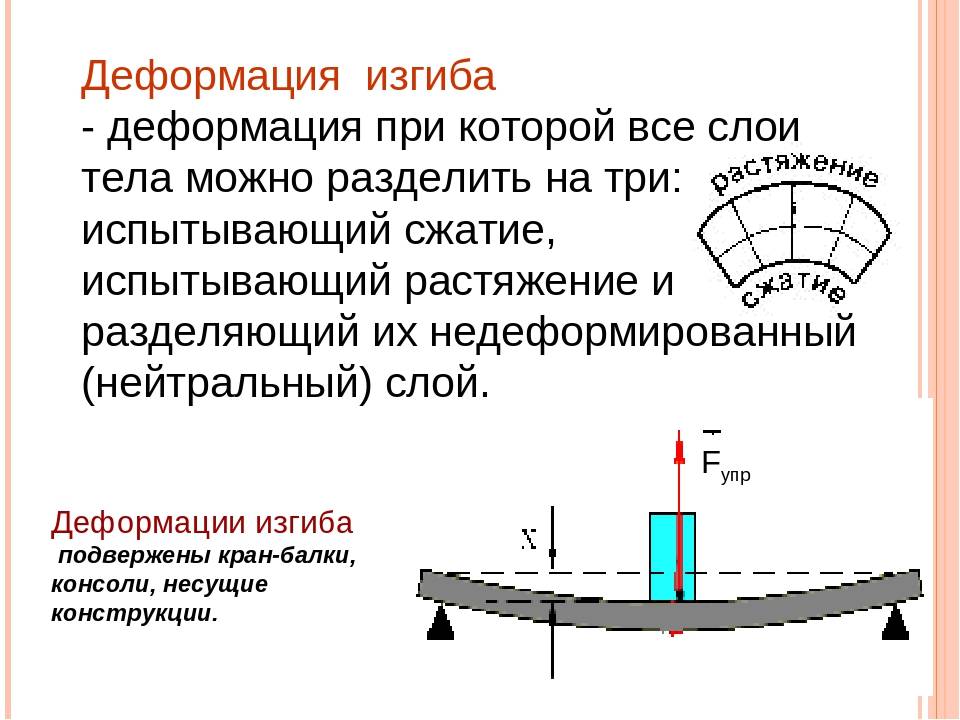
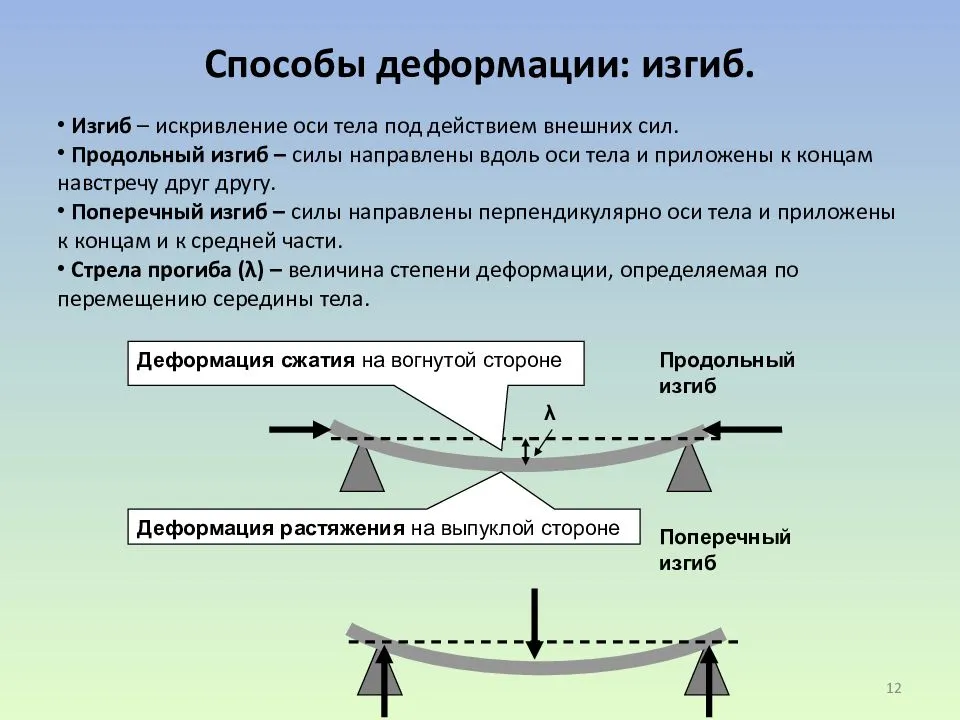
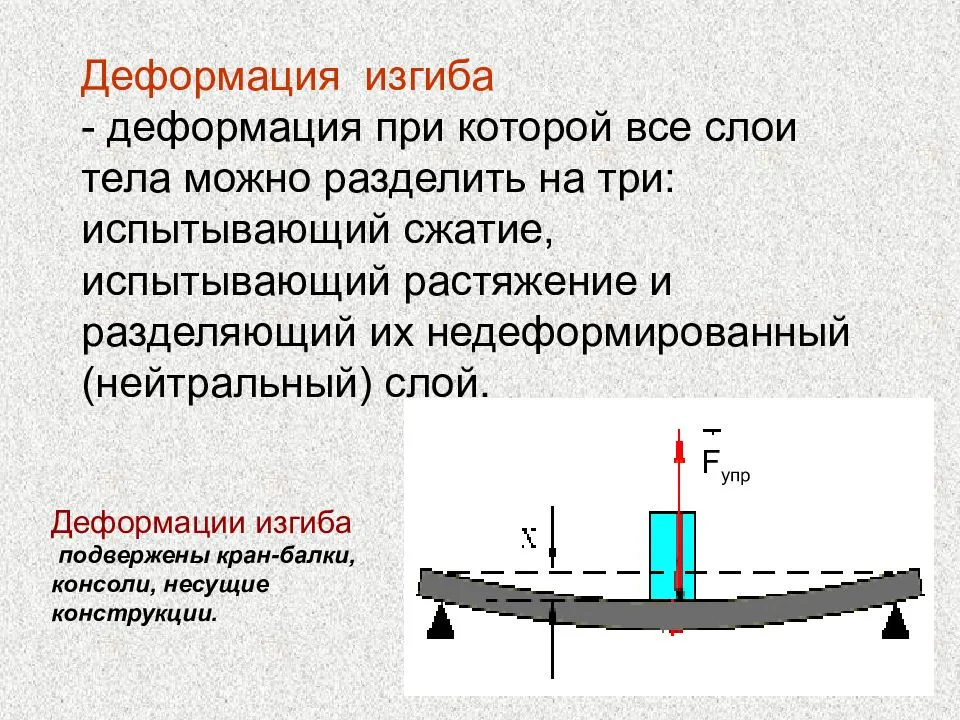
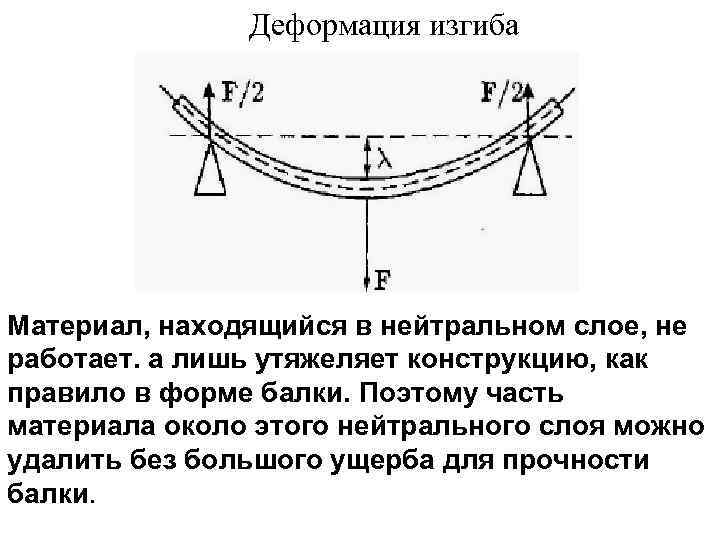
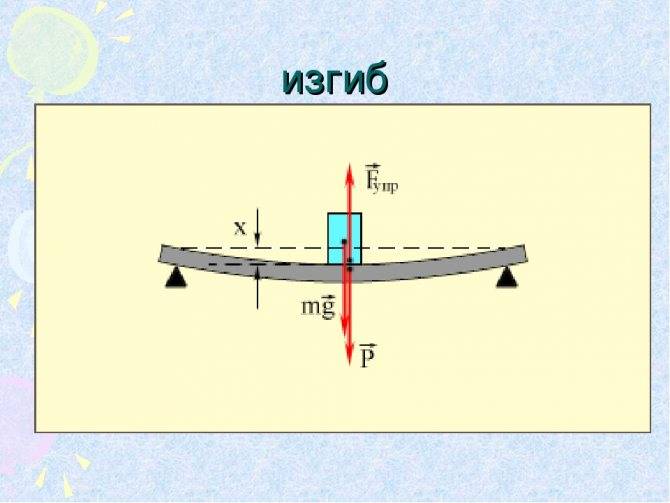
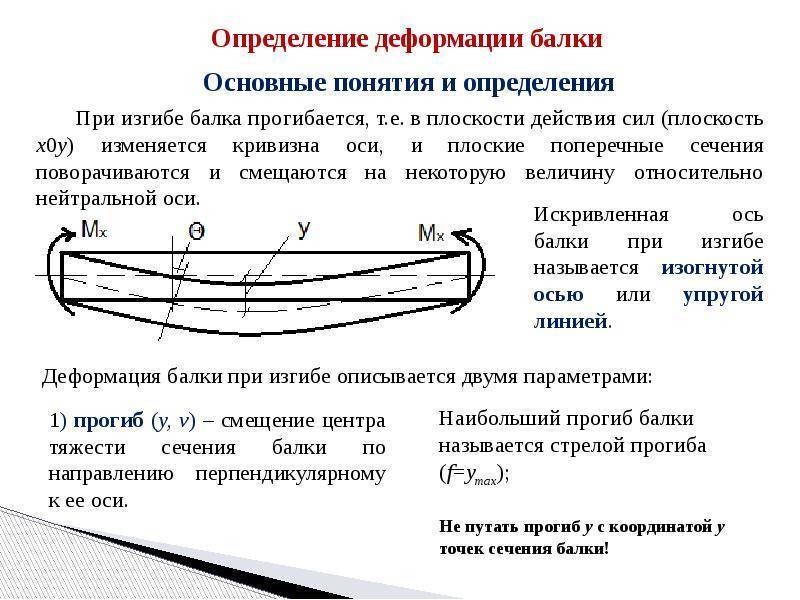
Чистый и поперечный изгиб балки

Если единственным внешним воздействием является сила, вызывающая изгибающий момент, такой изгиб называется чистым. Собственным весом изделия можно пренебречь.

При изгибе балки вводят следующие допущения:

• Во всех сечениях присутствуют только нормальные напряжения.
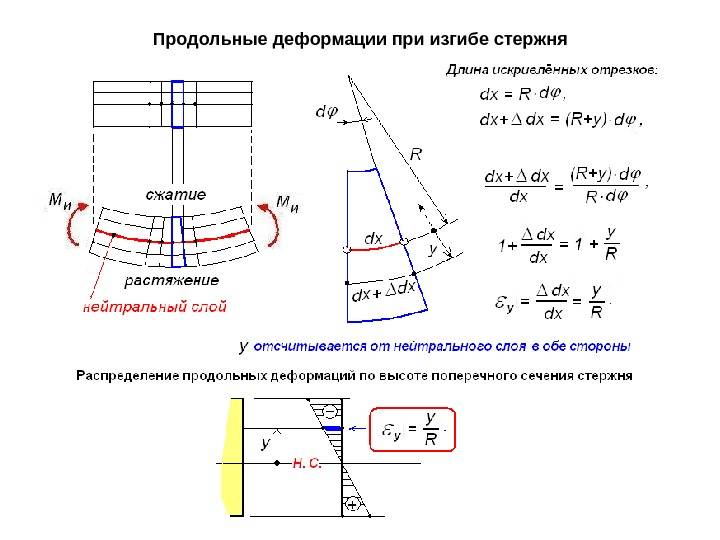
• Их разбивают на два слоя. Один называются растянутым, другой сжатым. Границей этих зон является линия сечения. Величина нормальных напряжений нейтрального слоя равны нулю.
• Продольный элемент детали подвержен осевому напряжению. Оно вызывает растяжение или сжатие. Соседние слои не вступают во взаимодействие друг с другом.
• При сохранении геометрической формы верхнего слоя все внутренние слои сохраняют прежнюю форму. Воздействие внешней силы остаётся перпендикулярным к поверхности детали.

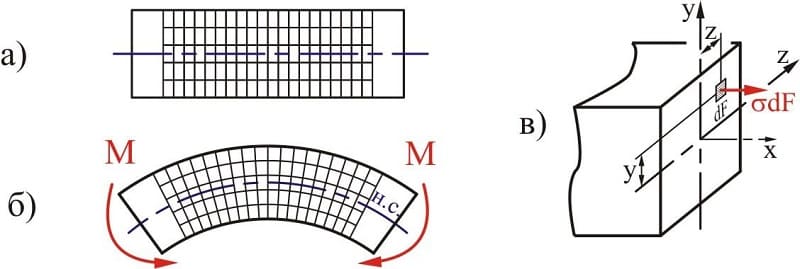
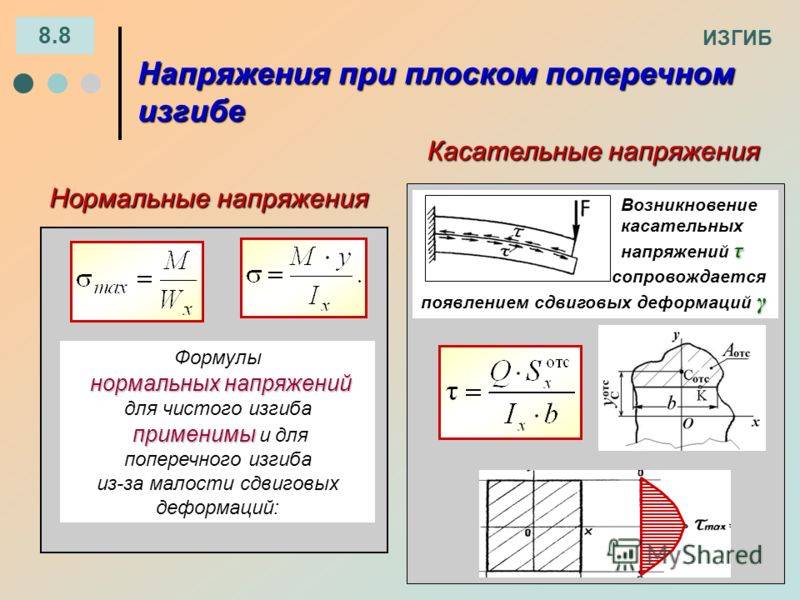
Если на поверхность детали производится воздействие под углом к поверхности — такой изгиб называется поперечным. При поперечном изгибе в слоях детали (например, балки) возникают два вида напряжений. Одни называются нормальными, другие касательными. В этом случае все сечения не будут плоскими, но искривлёнными. На определённых уровнях искривления при изгибе не достаточно большие. Это позволяет при расчёте применять все формулы, справедливые для чистого изгиба.

Продольные и поперечные деформации. Закон Гука

Иметь представление о продольных и поперечных деформациях и их связи.

Знать закон Гука, зависимости и формулы для расчета на­пряжений и перемещений.

Уметь проводить расчеты на прочность и жесткость ста­тически определимых брусьев при растяжении и сжатии.

Деформации при растяжении и сжатии

Рассмотрим деформацию бруса под действием продольной силы F (рис. 4.13).

Начальные размеры бруса: — начальная длина, — начальная ширина. Брус удлиняется на величину Δl; Δ1— абсолютное удлинение. При растя­жении поперечные размеры уменьшают­ся, Δ а — абсолютное сужение; Δ1 > 0; Δ а 0.

В сопротивлении материалов приня­то рассчитывать деформации в относи­тельных единицах: рис.4.13

— относительное удлинение;

Относительное сужение.

Между продольной и поперечной деформациями существует зависимость ε′=με, где μ – коэффициент поперечной деформации, или коэффициент Пуассона, — характеристика пластичности материала.

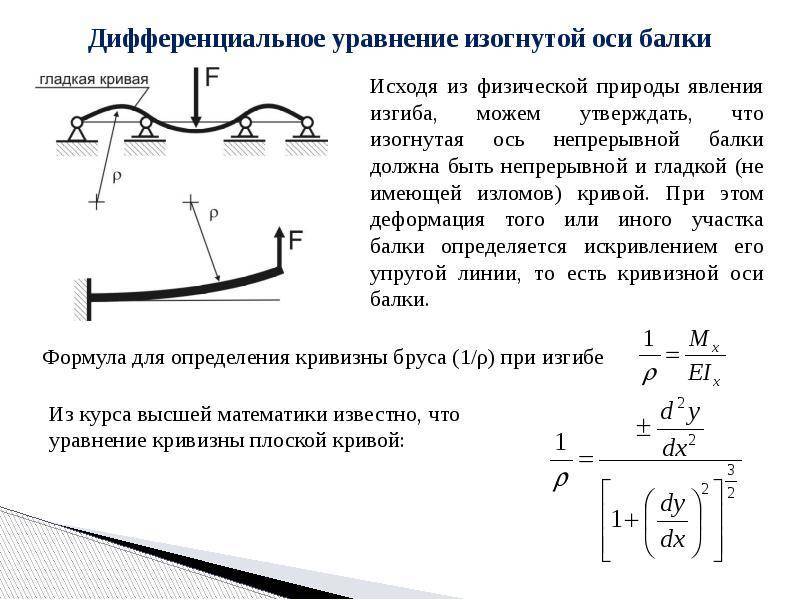
Расчёты на крепость при изгибе

Особенную важность во время проектирования конструкций и их индивидуальных элементов играют первичные расчёты на крепость при появляющихся изгибах. По результатам проведенных расчётов устанавливают фактические (настоящие) и возможные напряжения, которые могут выдержать детали и вся система в общем

Это позволит найти настоящий служебный срок создать советы по адекватной эксплуатации разработанного объекта.

Требование прочности выводится в результате сравнение 2-ух критериев. Самого большого напряжения, которое появляется в поперечном сечении при эксплуатировании и возможного напряжения для определенного элемента. Крепость зависит от применённого материала, размера детали, способа обработки и его физико-механических и химических параметров.

С целью решения установленной задачи используются методы и математический аппарат, разработанный в дисциплинах техническая механика, материаловедение и сопротивление материалов. В данном случае используются:

• дифференциальные зависимости Журавского (семейство дифференциальных уравнений связывающие важные параметры при деформации и их производные);
• способы определения перемещения (самыми эффективными считаются метод Мора и правило Верещагина);
• семейство принятых гипотез;
• разработанные правила построения графических изображений (построение эпюр).

Расчёт показателей изготавливается в три момента:

• при проверочном расчёте (вычисляют величину самого большого напряжения);
• на шаге проектирования (выполняется выбор толщины и показателей сечения бруса);
• во время вычисления допустимой нагрузки.

Полученные знаки величин стрессов определяются на основании оценки протекающих физических процессов и направления проекций векторов сил и факторов.

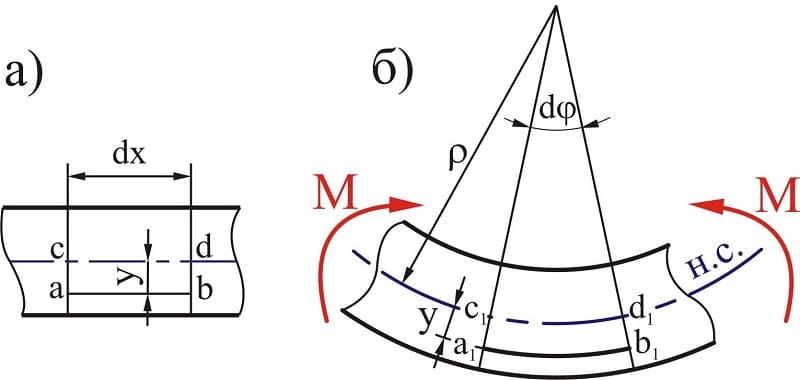
Наиболее наглядными результатами расчёта являются возведенные эпюры на поверхности разрабатываемого изделия. Они отражают воздействие всех силовых факторов на самые разнообразные слои деталей. При чистом изгибе эпюры имеют следующие характерности:

• на участке исследуемой балки с отсутствием нагрузки, которая носит распределённый характер, эпюра изображается прямой линией;
• на участке приложения называемых по другому сосредоточенных сил на эпюре встречается изменение направления в форме скачка в том месте к которому приложен вектор силы;
• в точке возникновения приложенного момента, скачок равён величине данного параметра;
• на участке с распределённой нагрузкой интенсивность влияния меняется по линейному закону, а поперечные нагрузки носят степенной характер изменения (очень часто по параболической кривой, с направлением выпуклости в сторону приложенной нагрузке);
• в пределах исследуемого участка функция изгибающего момента приобретает экстремум (на основании методов исследования функций при помощи дифференциального исчисления можно поставить характер экстремума – максимум или минимум).

В работе решение систем дифференциальных уравнений может вызвать настоящие сложности. По этому при расчётах допускаются некоторые прощения, которые не оказывают влияние на точность определяемых показателей. К этим упрощениям относятся:

• расчёт делают с учитыванием нормальных стрессов;
• в качестве основополагающего предположения принимают гипотезу о плоских сечениях;
• продолговатые волокна не делают дополнительного давления между собой (это дает возможность считать, что процессы изгиба носят линейный характер);
• дефармация волокон не зависит от их ширины (значения нормальных стрессов частые по всей ширине);
• для расчётной балки задают одну поверхность симметрии (все наружные силы лежат в данной плоскости);
• физико-механические свойства материалов подчиняются закону Гука (модуль упругости имеет постоянную величину);
• процессы в балке подчиняются законам плоского изгиба (это допущение вытекает из соотношений геометрических размеров изделия).

Сегодняшние методы исследования влияния внешних сил, внутренних стрессов и факторов дают возможность с большой степенью точности высчитать крепость каждой детали и всей конструкции в общем. Использование компьютерных методов расчёта, фрактальной геометрии и 3D графики дает возможность получить детальную картину происходящих процессов.

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.

Закон Гука

Математические расчеты, необходимые в строительстве, технике, позволили применять закон Гука для деформации сдвига. Формула показывала прямую связь между силой, прикладываемой к телу, и его удлинением (сжатием). Гук использовал коэффициент жесткости, показывая связь между материалом и возможностью его деформации.

По мере развития и совершенствования технических средств, аппаратов и приборов, разработки теории сопротивления, были проведены серьезные исследования пластичности и упругости. Результаты проведенных фундаментальных экспериментов стали применять в строительной технике, теории сооружений, теоретической механике.

Благодаря комплексному подходу к проблемам, связанным с различными видами деформации, удалось развить строительную отрасль, осуществлять профилактику правильной осанки у подрастающего поколения страны.

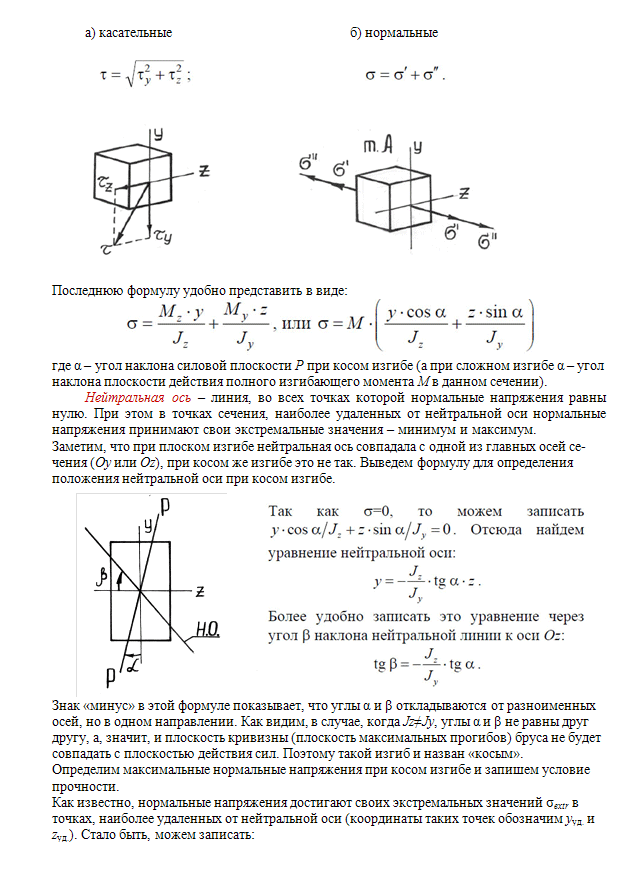
Внецентренное растяжение или сжатие.

При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса.

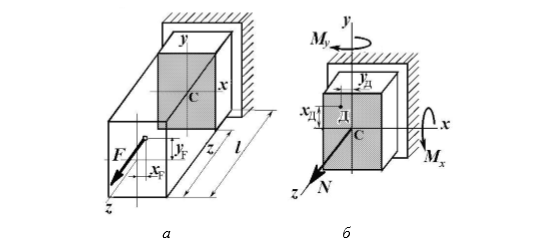
К расчёту на прочность бруса при внецентренном растяжении

a – нагружение бруса; б – внутренние силовые факторы в поперечном сечении;

Приведём силу F к центру тяжести:

где у_F , x_F — координаты точки приложения силы F.

В произвольной точке Д, с координатами (х_д, у_д), нормальное напряжение определяется по фомуле:

Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид:

Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям.

Сдвиг фаз переменного тока и напряжения

Мощность постоянного тока, как мы уже знаем, равна про­изведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При пере­менном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденса­торов и катушек индуктивности.

Для этого случая формула мощности

На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают)

Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы

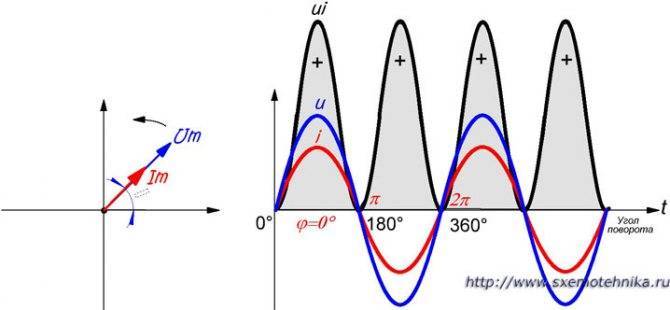
Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.

При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.

О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.

Представим себе, что при начале вращения радиусы-век­торы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.

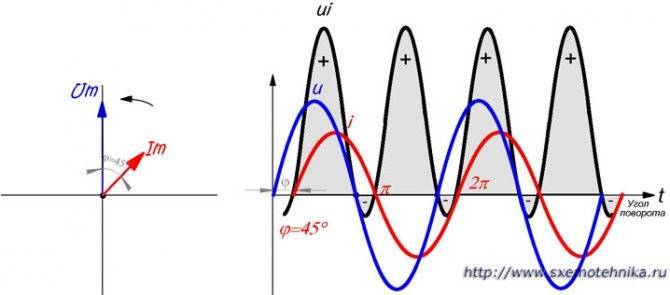
Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.

Рассмот­рим, как будут изменяйся при этом ток и напряжение. Из по­строенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.

Затем напряжение достигает своей наибольшей ве­личины и начинает уже убывать, а ток хотя и становится по­ложительным, но еще не достигает наибольшей величины и продолжает возрастать. Напряжение изменило свое направле­ние, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряже­ния. Между фазами напряжения и тока существует постоян­ный сдвиг, называемый сдвигом фаз.

Действительно, если мы посмотрим на рисунок 2, то заме­тим, что синусоида тока сдвинута вправо относительно сину­соиды напряжения. Так как по горизонтальной оси мы откла­дываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.

Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с на­правлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величи­ны на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источни­ком ее. Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.

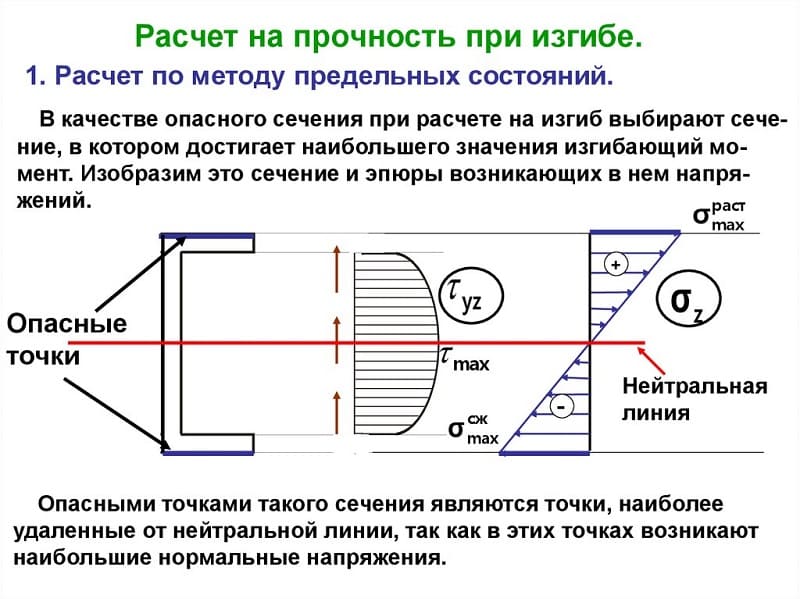
Расчёты на прочность при изгибе

Особую важность при проектировании конструкций и их отдельных элементов играют предварительные расчёты на прочность при возникающих изгибах. По результатам проведенных расчётов устанавливают фактические (реальные) и допустимые напряжения, которые способны выдержать элементы и вся конструкция в целом. Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта

Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта.

Условие прочности выводится в результате сравнения двух показателей. Наибольшего напряжения, которое возникает в поперечном сечении при эксплуатации и допустимого напряжения для конкретного элемента. Прочность зависит от применённого материала, размера детали, способа обработки и его физико-механических и химических свойств.

Для решения поставленной задачи применяются методы и математический аппарат, разработанный в дисциплинах техническая механика, материаловедение и сопротивление материалов. В этом случае применяются:

• дифференциальные зависимости Журавского (семейство дифференциальных уравнений связывающие основные параметры при деформации и их производные);
• способы определения перемещения (наиболее эффективными считаются метод Мора и правило Верещагина);
• семейство принятых гипотез;
• разработанные правила построения графических изображений (построение эпюр).

Расчёт параметров производится в три этапа:

• при проверочном расчёте (вычисляют величину максимального напряжения);
• на этапе проектирования (производится выбор толщины и параметров сечения бруса);
• во время вычисления допустимой нагрузки.

Полученные знаки величин напряжений определяются на основании оценки протекающих физических процессов и направления проекций векторов сил и моментов.

Наиболее наглядными результатами расчёта являются построенные эпюры на поверхности разрабатываемого изделия. Они отражают влияние всех силовых факторов на различные слои деталей. При чистом изгибе эпюры имеют следующие особенности:

• на участке исследуемой балки с отсутствием нагрузки, которая носит распределённый характер, эпюра изображается прямой линией;
• на участке приложения так называемых сосредоточенных сил на эпюре наблюдается изменение направления в форме скачка в том месте к которому приложен вектор силы;
• в точке появления приложенного момента, скачок равен величине этого параметра;
• на участке с распределённой нагрузкой интенсивность воздействия изменяется по линейному закону, а поперечные нагрузки носят степенной характер изменения (чаще всего по параболической кривой, с направлением выпуклости в сторону приложенной нагрузке);
• в границах исследуемого участка функция изгибающего момента приобретает экстремум (на основании методов исследования функций с помощью дифференциального исчисления можно установить характер экстремума – максимум или минимум).

На практике решение систем дифференциальных уравнений может вызвать определённые трудности. Поэтому при расчётах допускаются некоторые прощения, которые не влияют на точность определяемых параметров. К этим упрощениям относятся:

• расчёт производят с учётом нормальных напряжений;
• в качестве основного предположения принимают гипотезу о плоских сечениях;
• продольные волокна не производят дополнительного давления между собой (это позволяет считать, что процессы изгиба носят линейный характер);
• деформация волокон не зависит от их ширины (значения нормальных напряжений постоянные по всей ширине);
• для расчётной балки задают одну плоскость симметрии (все внешние силы лежат в этой плоскости);
• физико-механические характеристики материала подчиняются закону Гука (модуль упругости имеет постоянную величину);
• процессы в балке подчиняются законам плоского изгиба (это допущение вытекает из соотношений геометрических размеров изделия).

Современные методы исследования воздействия внешних сил, внутренних напряжений и моментов позволяют с высокой степенью точности рассчитать прочность каждой детали и всей конструкции в целом. Применение компьютерных методов расчёта, фрактальной геометрии и 3D графики позволяет получить подробную картину происходящих процессов.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) – сила упругости;

( Delta L left(text{м} right) ) – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

Подставим в это уравнение выражение для силы упругости

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:

(g) – ускорение свободного падения, оно связано с силой тяжести.