Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
m=t/π,
где t — шаг.
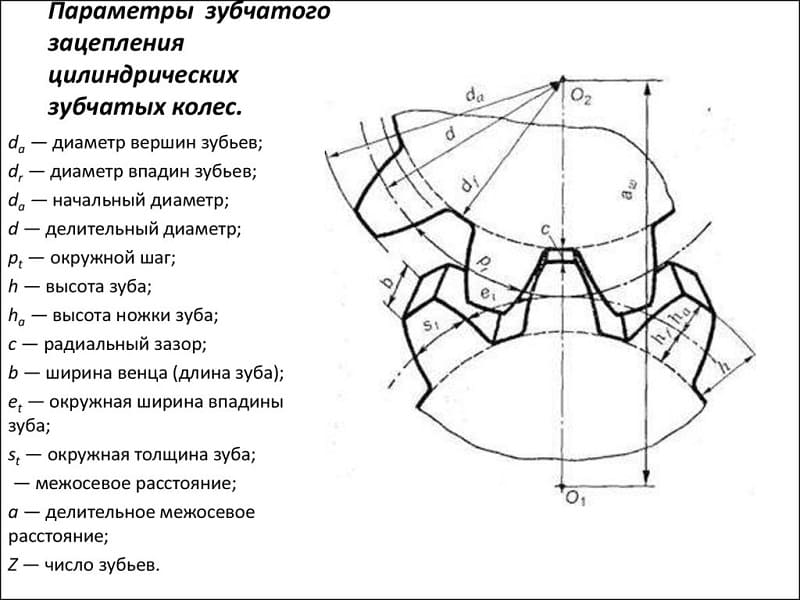
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
m=h/2,25,
где h — высота зубца.
И, наконец,
m=De/(z+2),
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Основные ошибки самостоятельной замены
Несмотря на предельно простую технологию, автолюбители часто допускают при замене венца следующие ошибки:
- перед тем, как снять зубчатый обод, следует произвести ревизию боковой плоскости маховика под сцепление, и отверстий для крепежных болтов;
- установка с перегревом отдельных участков венца приведет к быстрому износу зубьев именно на этих местах, так как происходит отпуск стали;
- наружный диаметр зубьев должен иметь фаску для плавного зацепления с бендиксом стартера без ударов.
Для того, чтобы уменьшить износ двигателя и увеличить приемистость машины на высоких оборотах, маховик часто облегчают. Из-за наличия дополнительных отверстий на наружном диаметре диска в зоне, примыкающей к зубчатому ободу, венец часто приваривается к диску.
Таким образом, венец можно заменить собственными силами при значительной выработке профиля зуба на отдельных участках. Снять обод можно на холодную, а при установке потребуется нагрев до 200 градусов максимум.
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
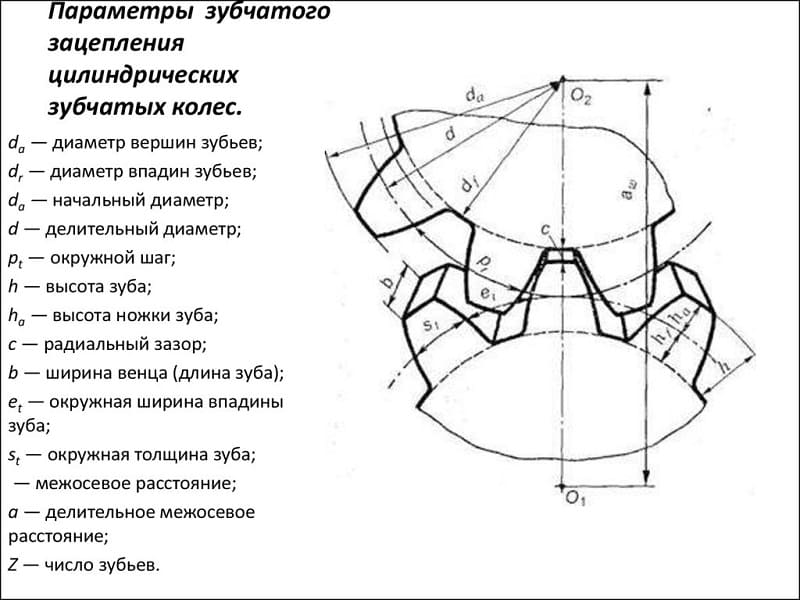
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Геометрический расчет элементов цилиндрической зубчатой передачи
Исходные данные для расчета:
- Модуль m = 4 мм;
- Число зубьев шестерни Z1 = 18;
- Число зубьев колеса Z2 = 30;
- Диаметр вала (ведущий) DB1 = 22 мм;
- Тип шпонки – Призматическая;
- Число шлицев Z – 8;
- Внутренний диаметр шлицев d = 22 мм;
- Диаметр вала (ведомый) DB2 = 30 мм;
- Ширина шлица b = 6 мм;
- Тип – D.
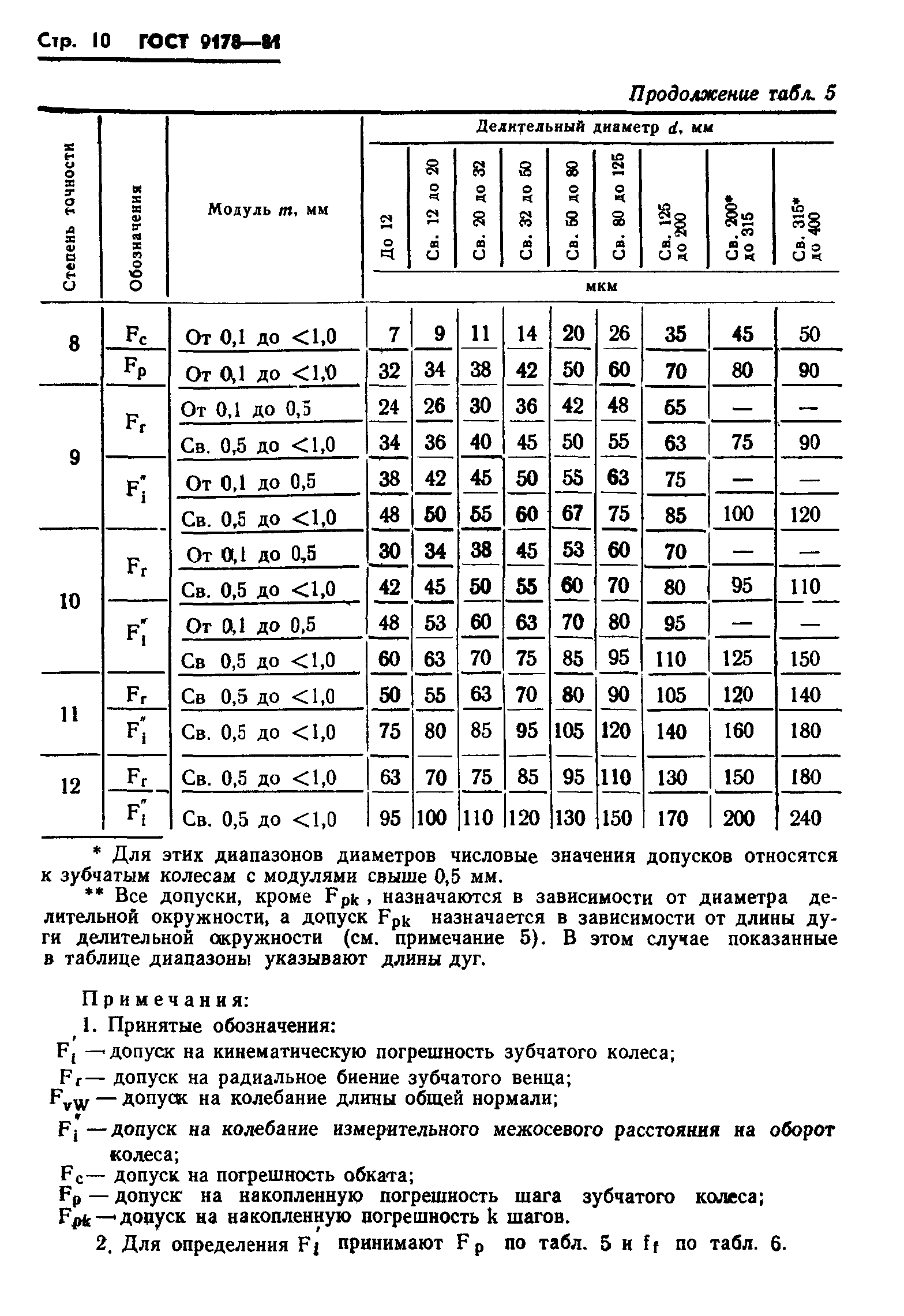
Результаты геометрического расчета цилиндрической зубчатой передачи
- Делительный диаметр шестерни d1=mz1=4×18=72 мм;
- Делительный диаметр колеса d2=mz2=4×30=120 мм;
- Высота головки зуба ha=m =4 мм;
- Высота ножки зуба hf=1,25m=1,25×4=5 мм;
- Высота зуба h=ha+hf=2,25m=2,25×4=9 мм;
- Диаметр вершин зубьев шестерни da1=d1+2ha1=72+2×4=80 мм;
- Диаметр впадин шестерни df1=d1-2hf=72-2×5=62 мм;
- Длина ступицы шестерни Lст1=1,5DB1=1,5×22=33 мм;
- Наружный диаметр ступицы шестерни Dст1=1,6DB1=1,6×22=35,2 мм;
- Диаметр вала шестерни D1=1,2×22=26,4 мм;
- Делительный диаметр колеса d2=mz2=4×30=120 мм;
- Диаметр вершин зубьев колеса da2=d2+2ha=120+2×4=128 мм;
- Диаметр впадин колеса df2=d2-2hf2=120-2×5=110 мм;
- Длина ступицы колеса Lст2=1,5DB2=1,5×30=45 мм;
- Наружный диаметр ступицы колеса Dст2=1,6DB2=1,6×30=48 мм;
- Диаметр вала колеса D2=1,2DB2=1,2×30=36 мм;
- Ширина зубчатого венца b=6m=6×4=24 мм;
- Толщина обода зубчатого венца δ1=2,25m=2,25×4=9 мм;
- Толщина диска δ2=1/3b=8 мм;
- Межосевое расстояние a=0,5(d1+d2)=0,5(72+120)=96 мм;
- Длина шлицев Lшл=(1,5. 2)Lст2=(1,5. 2)45=72 мм.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
что соответствует формуле:
и если выполнить подстановку, то получим:
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
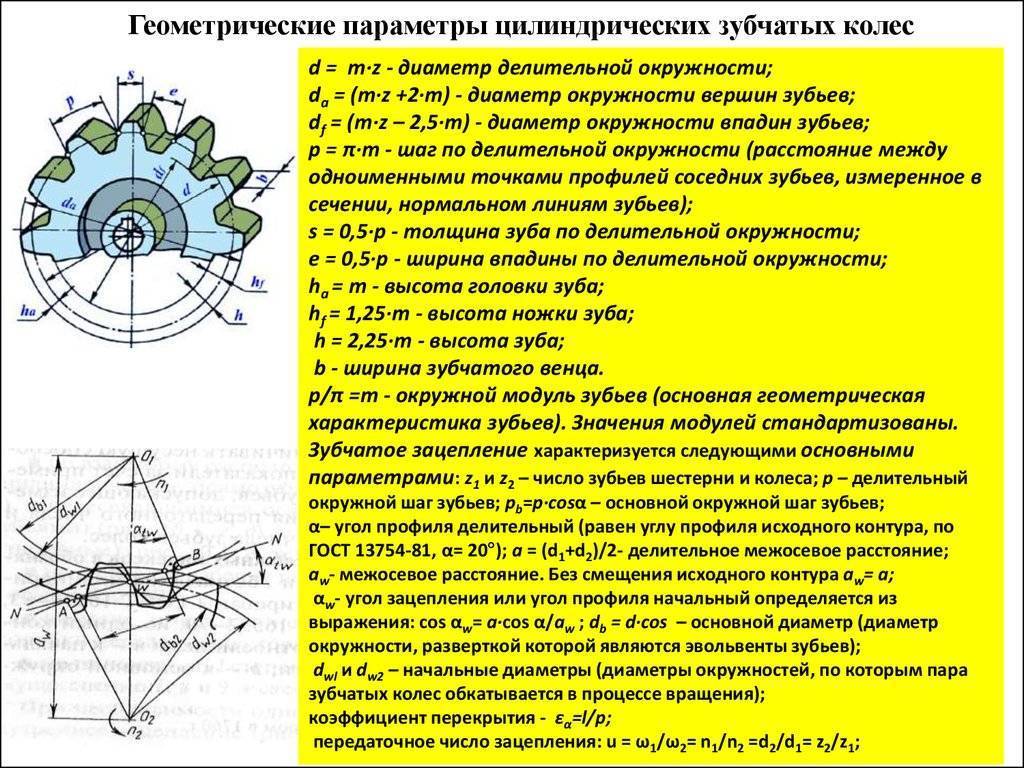
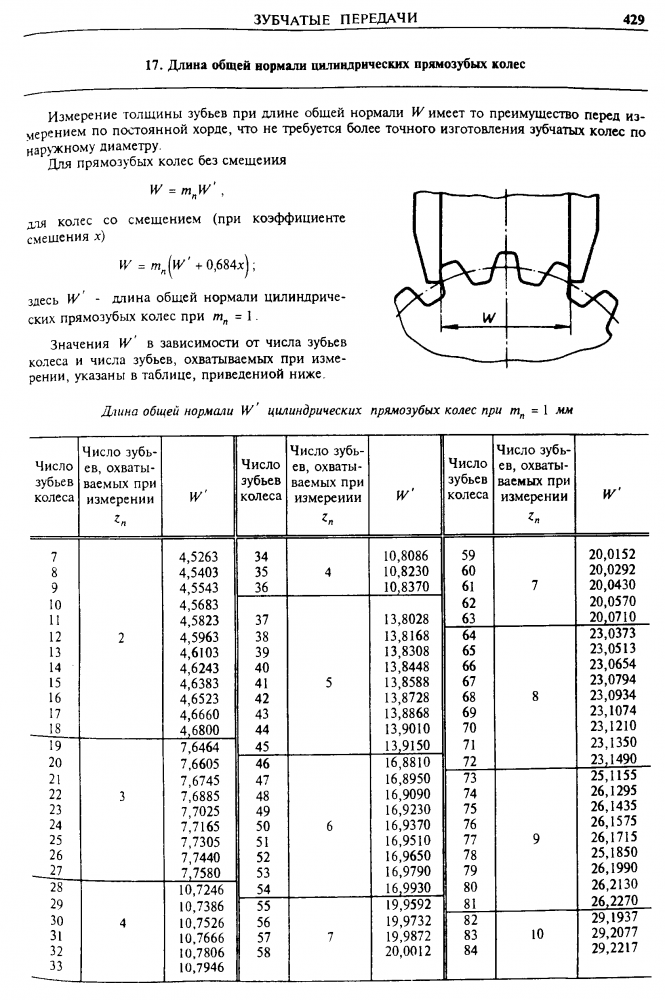
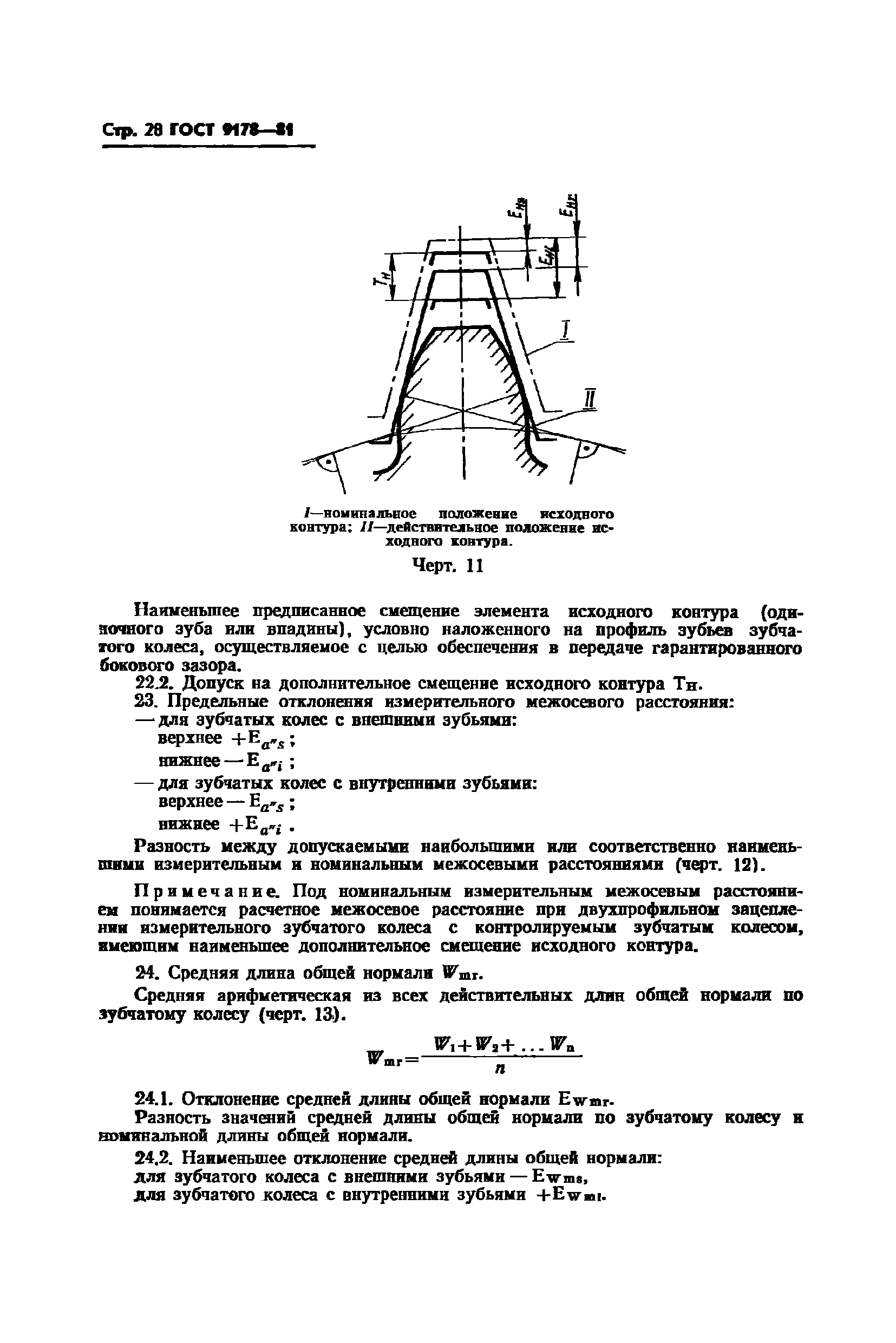
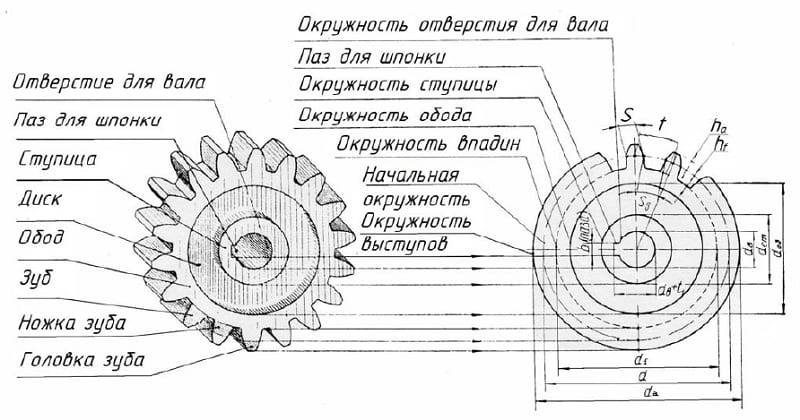
Для выполнения расчетов, чертежей и эскизов зубчатых колёс и других деталей зубчатых передач надо знать основные элементы и параметры зубчатых зацеплений и условности, принятые для изображения зубчатого венца.
Рис. 17. Шестерни с элементами фиксации на валу
Основным элементом зубчатого колеса является зуб. Начальная поверхность делит зуб по его высоте на две неравные части — головку и ножку. Часть зуба, расположенная над делительной поверхностью, называется головкой зуба, а расположенная ниже делительной поверхности — ножкой зуба. Зубья с ободом составляют венец зубчатого колеса, который через диск или спицы соединён со ступицей, имеющей отверстие для вала, зачастую с элементами фиксации колеса на валу, например, при помощи шпоночного (рис. 17, а) или шлицевого (рис. 17, б) соединений.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
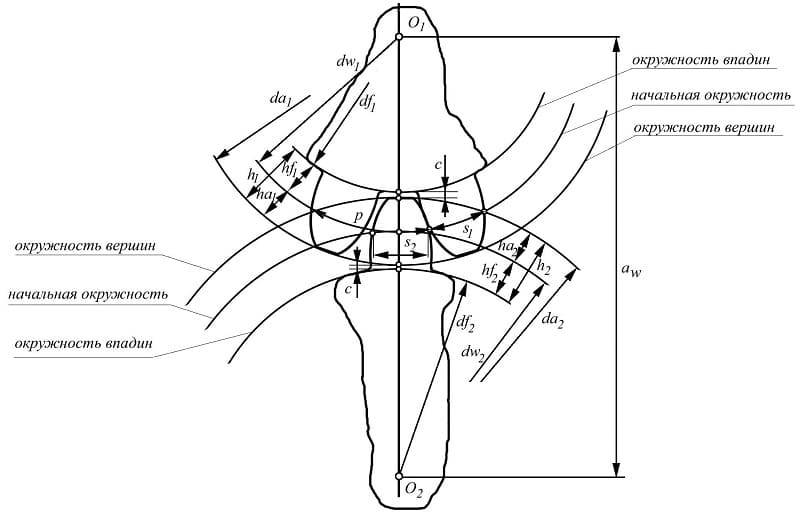
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них
Коэффициент запаса прочности при работе зуба двумя сторонами
например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др. | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
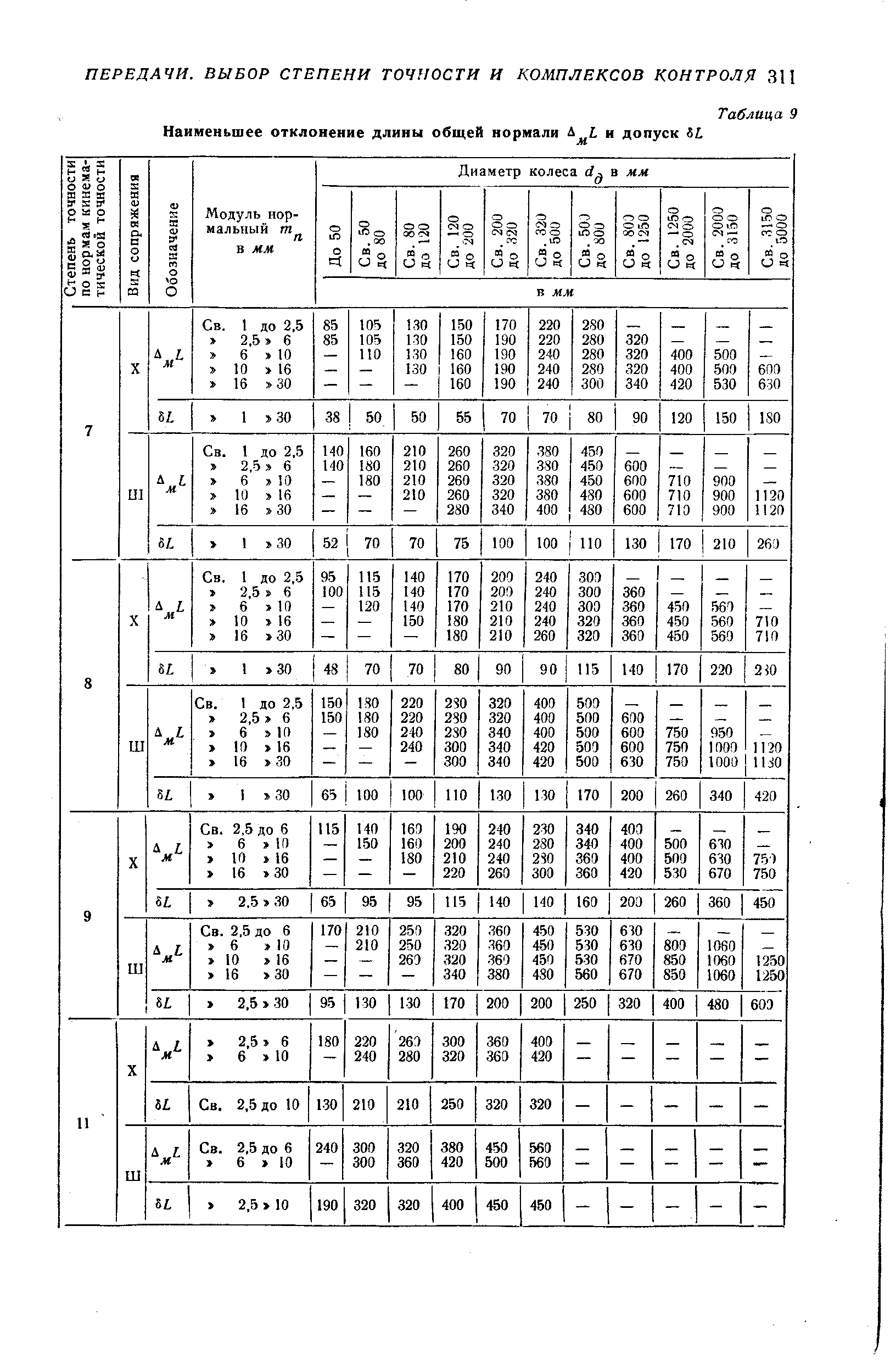
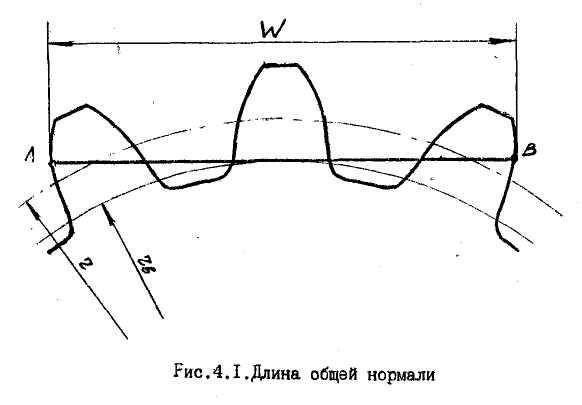
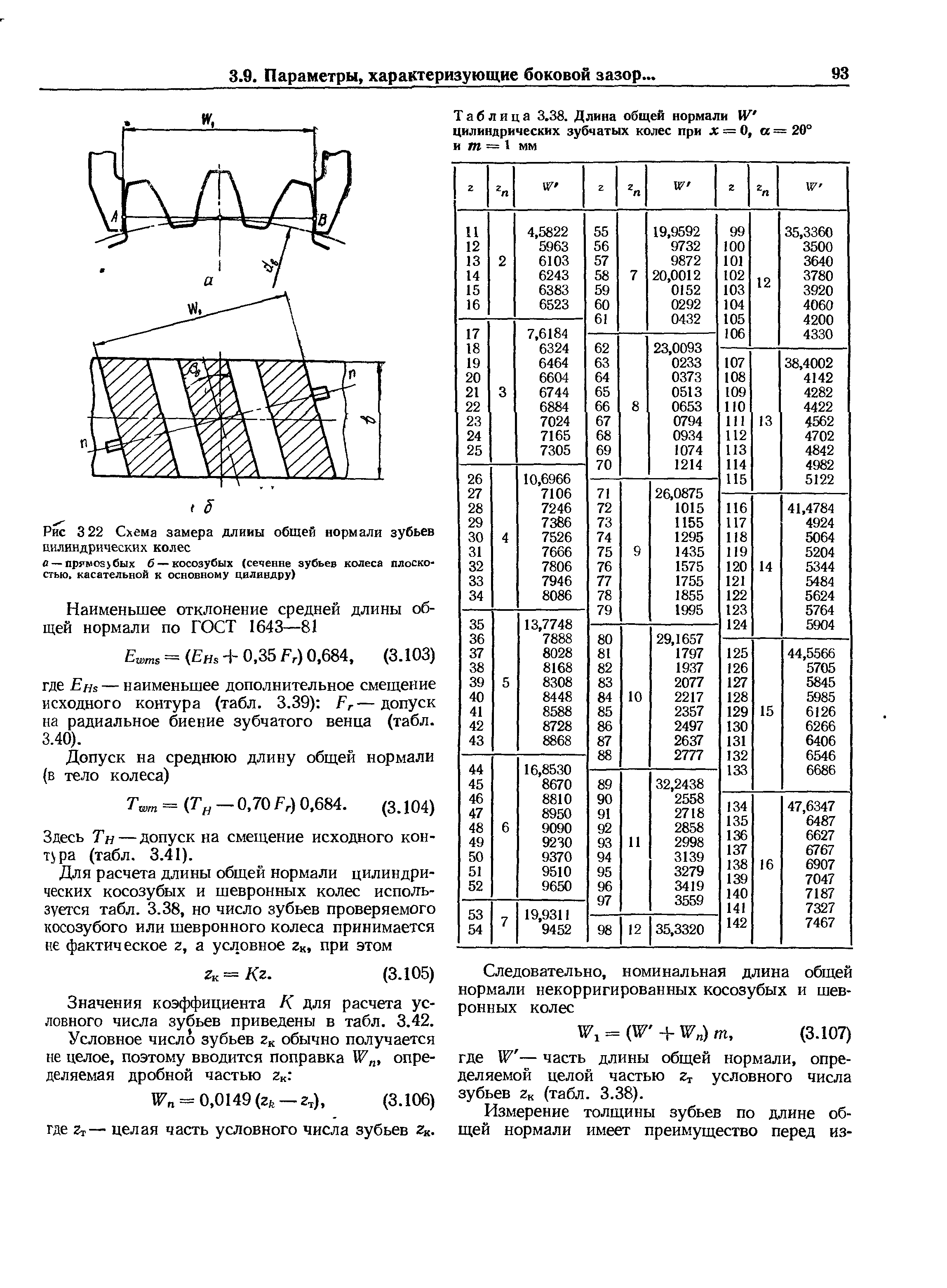
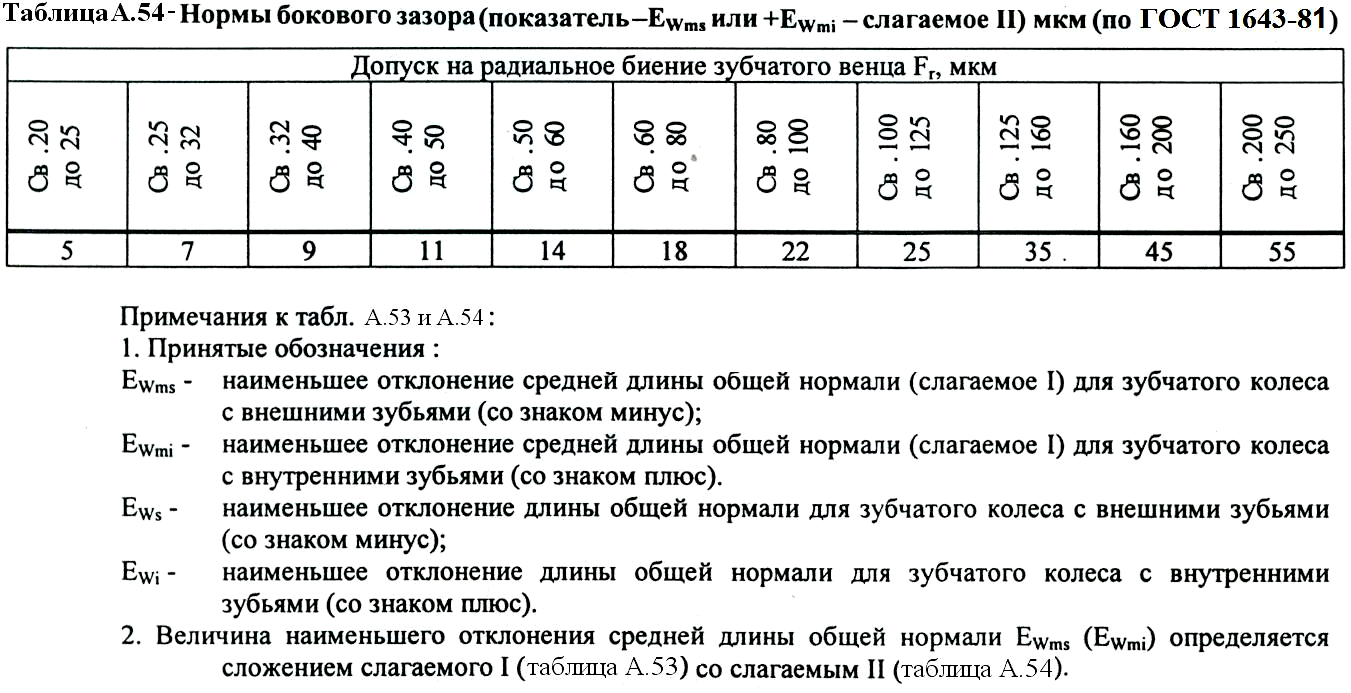
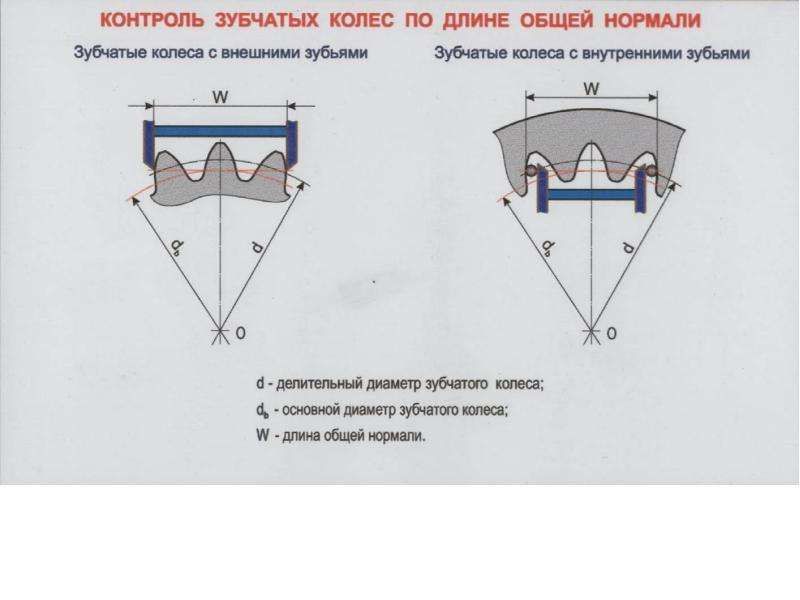
Колебание – длина – общая нормаль
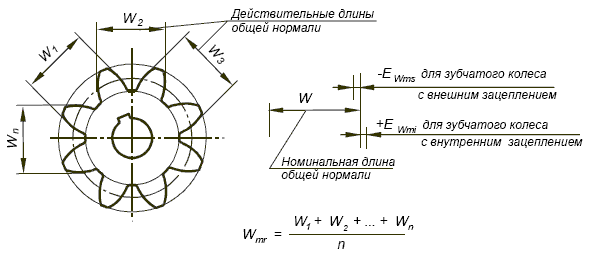
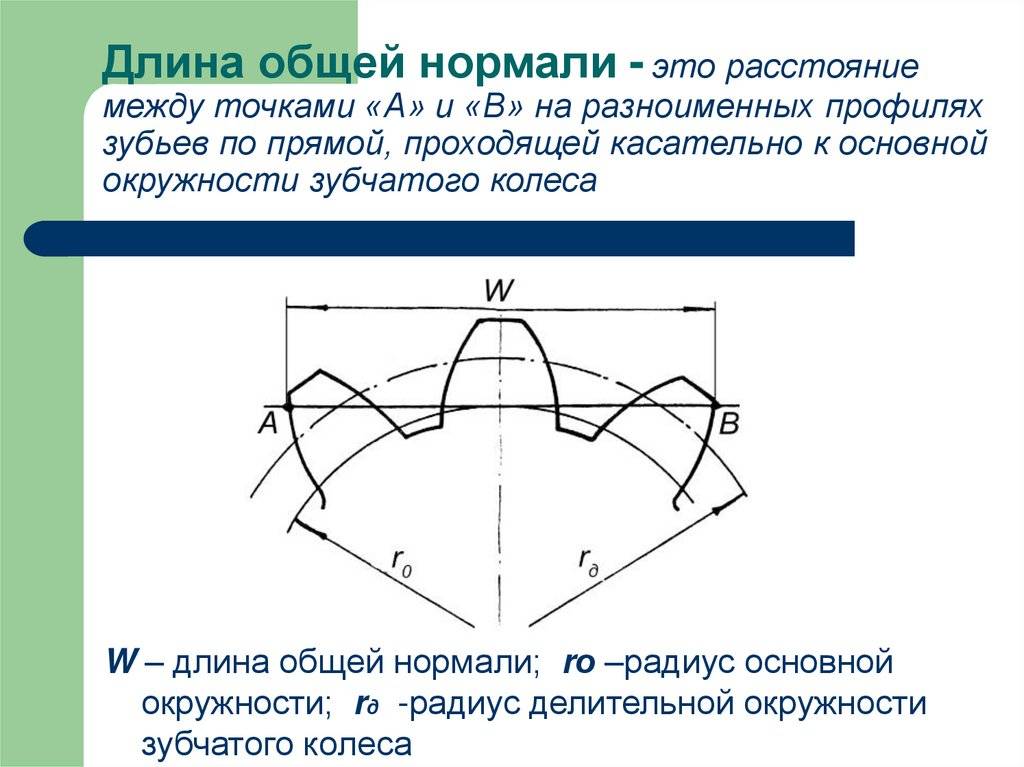
Колебание длины общей нормали ( Д0Ь) определяется разностью между наибольшей и наименьшей длиной общей нормали, полученной при измерении ее по всей окружности проверяемого зубчатого колеса.
Колебание длины общей нормали ( по окружности колеса) определяют как разность между наибольшей и наименьшей длиной нормали (
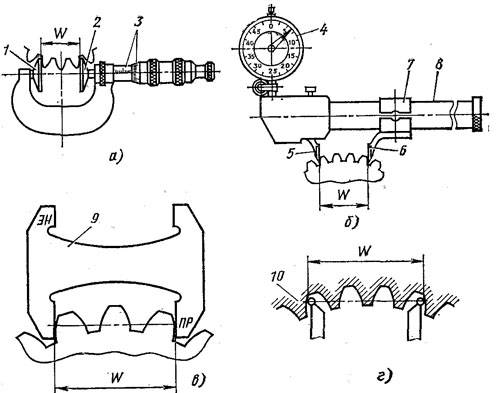
Колебание длины общей нормали L контролируют на приборах, имеющих два наконечника с параллельными плоскостями и в за-ьиеимости от требуемой точности отсчетное нониусное, микрометрическое 2 или индикаторное устройство. Особенностью контроля длины общей нормали является отсутствие необходимости базирования колеса по его оси.
Колебание длины общей нормали L контролируют на приборах, имеющих два наконечника о параллельными плоскостями и в зависимости от требуемой точности отсчетное нониусное, микрометрическое 2 или индикаторное устройство. Особенностью контроля длины общей нормали является отсутствие необходимости базирования колеса по его оси.
Колебание длины общей нормали Va r можно контролировать разным инструментом, у которого имеются две параллельные измерительные плоскости.
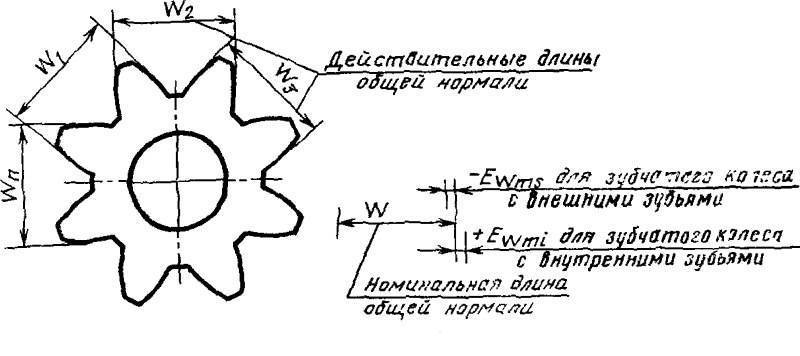
Колебание длины общей нормали F находят как разность между наибольшей и наименьшей действительными длинами общей нормали при последовательном измерении всех групп зубьев проверяемого колеса. Колебание длины общей нормали может быть показателем погрешности обката при зубообразовании.
| Кривая накопленной погрешности шага. |
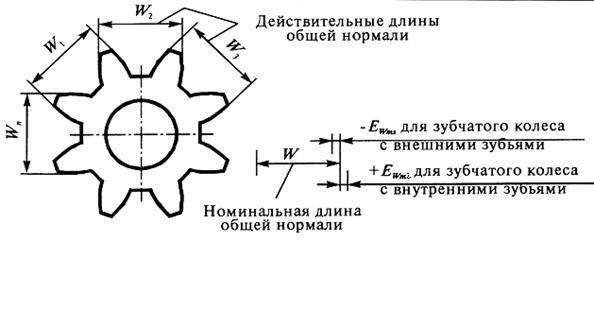
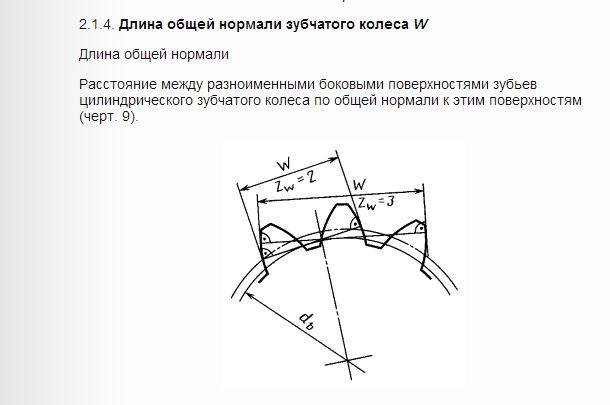
Колебанием длины общей нормали FVWr называется расстояние между двумя параллельными плоскостями касательными к двум разноименным активным боковым поверхностям зубьев зубчатого колеса.
На колебание длины общей нормали влияют лишь тангенциальные составляющие погрешности окружных шагов и не влияют радиальные. Поэтому для полной оценки колеса в отношении кинематической точности необходимо проконтролировать колесо и по одному из параметров, учитывающих радиальные составляющие погрешностей окружных шагов, например измерить радиальное биение.
| Кривая накопленной погрешности шага. |
Измерение колебания длины общей нормали проводится любым прибором, имеющим измерительные поверхности в виде параллельных плоскостей, например штангенциркулями.
Контроль колебания длины общей нормали производится на станковых приборах, имеющих специальные приспособления, или накладными – нормалемерами и микрометрическими скобами для зубчатых колес.
Величина колебания длины общей нормали 1UL определяется как разность наибольшей и наименьшей длины общей нормали при последовательном измерении всех групп зубьев по окружности колеса. В этом случае настройки по блоку плиток не требуется.
Контроль колебания длины общей нормали прост и не требует иметь какой-либо промежуточной измерительной базы. Часто производится измерение длины общей нормали, а не ее колебания. Это осуществляется с целью выяснения толщины зуба и рассматривается ниже.
Контроль колебания длины общей нормали может осуществляться с помощью микрометров ( фиг. Кирове ( КРИН), у которых в отличие от обычного микрометра имеются тарельчатые измерительные поверхности. Недостатком микрометров является то, что одна измерительная поверхность вращается и при соприкосновении с контролируемой поверхностью несколько увлекает весь прибор. Для контроля колебаний длины общей нормали более удобен прибор конструкции завода ЛИЗ ( фиг. Для колес средних размеров контроль колебания длины общей нормали удобно производить с помощью индикаторных скоб ( фиг.