Геометрический расчет зубчатой передачи выполним в программе MS Excel
При отсутствии у вас на компьютере программы MSExcel воспользуйтесь бесплатной программой OOoCalc из пакета OpenOffice.
Целью данного расчета является нахождение ряда размеров (углов и диаметров), необходимых для окончательного оформления рабочих чертежей колеса и шестерни, а так же для выполнения в дальнейшем проверочных расчетов качества зубчатого зацепления по геометрическим показателям.
Ссылка на файл с программой – в конце статьи.
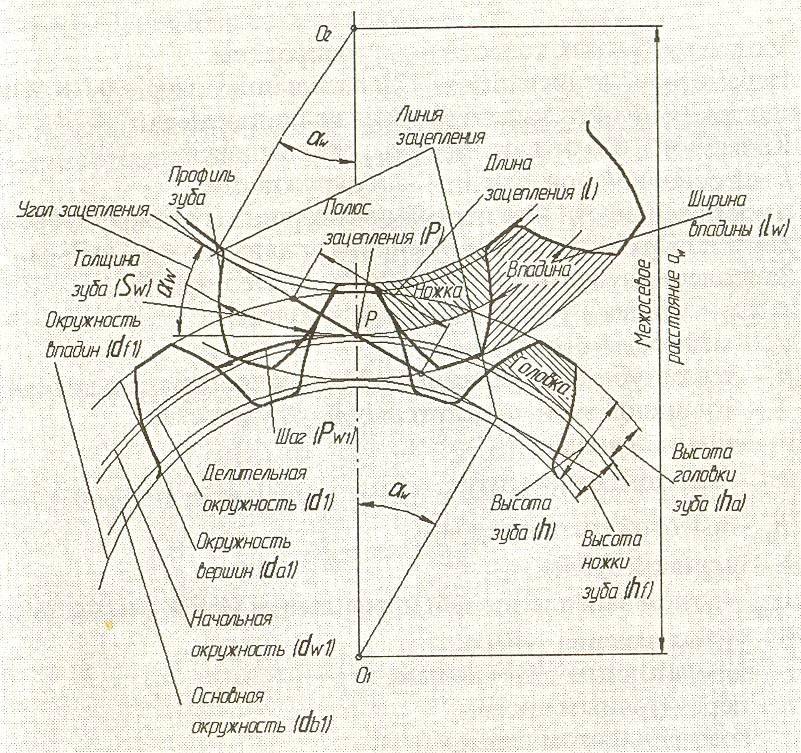
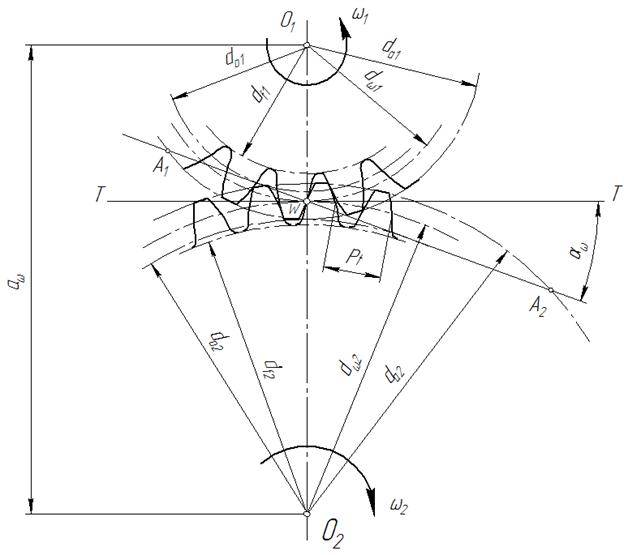
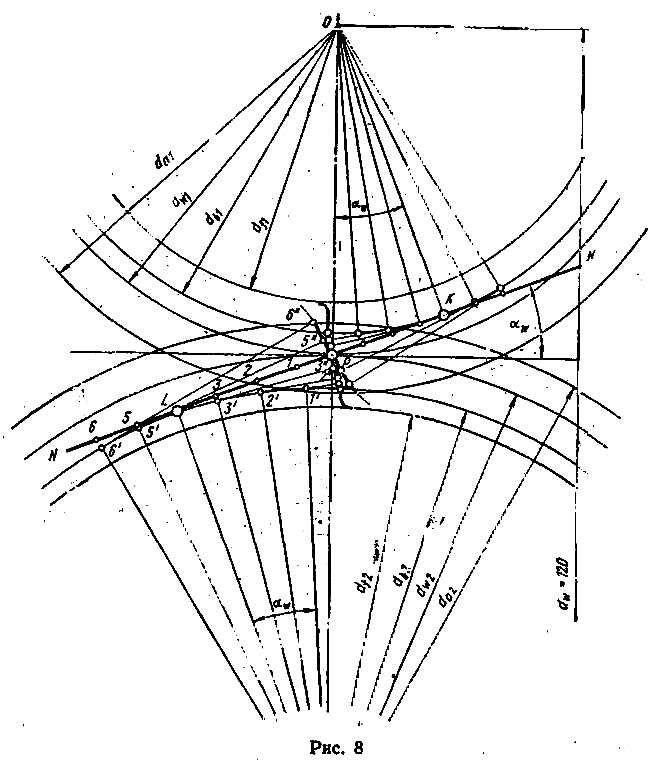
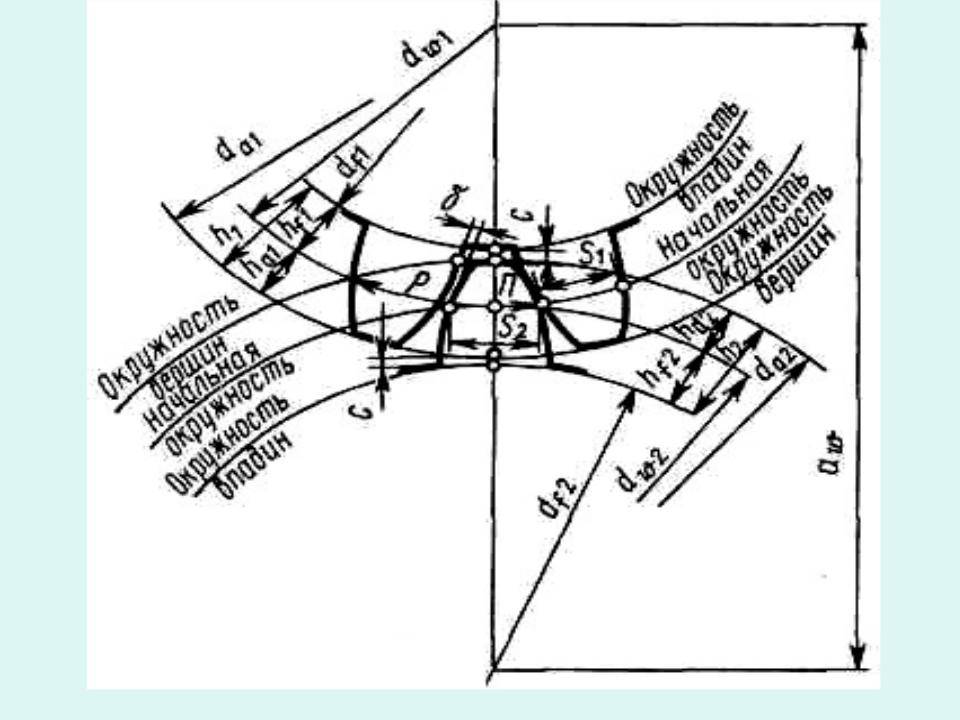
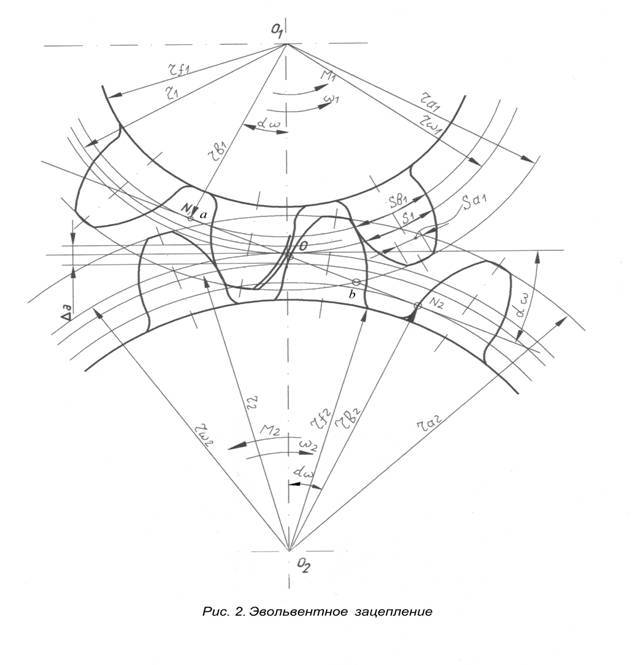
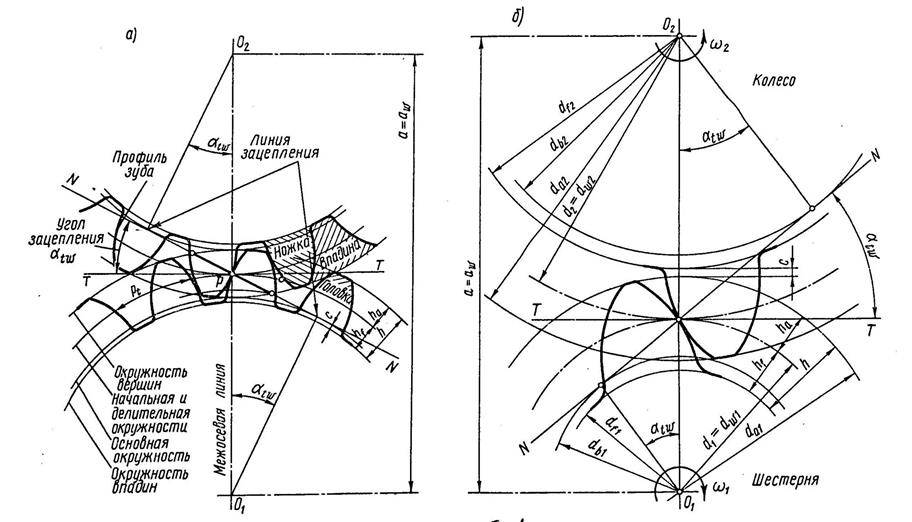
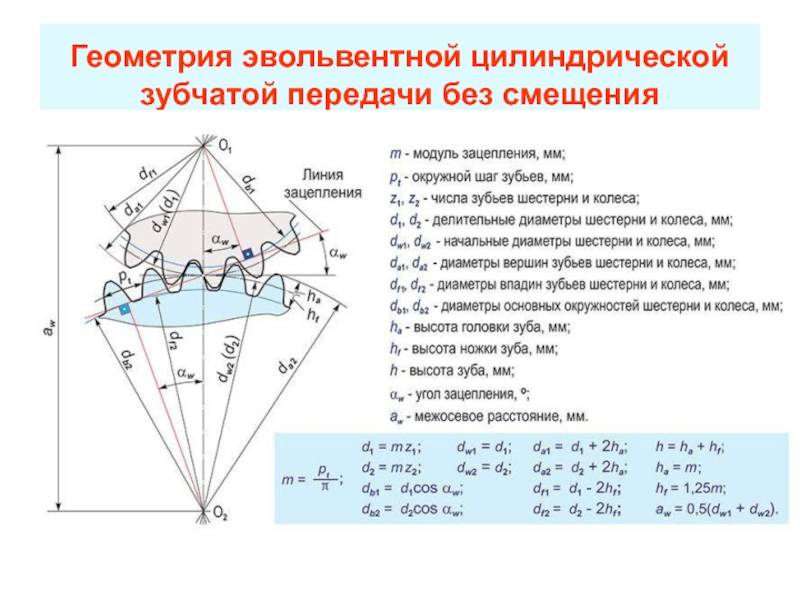
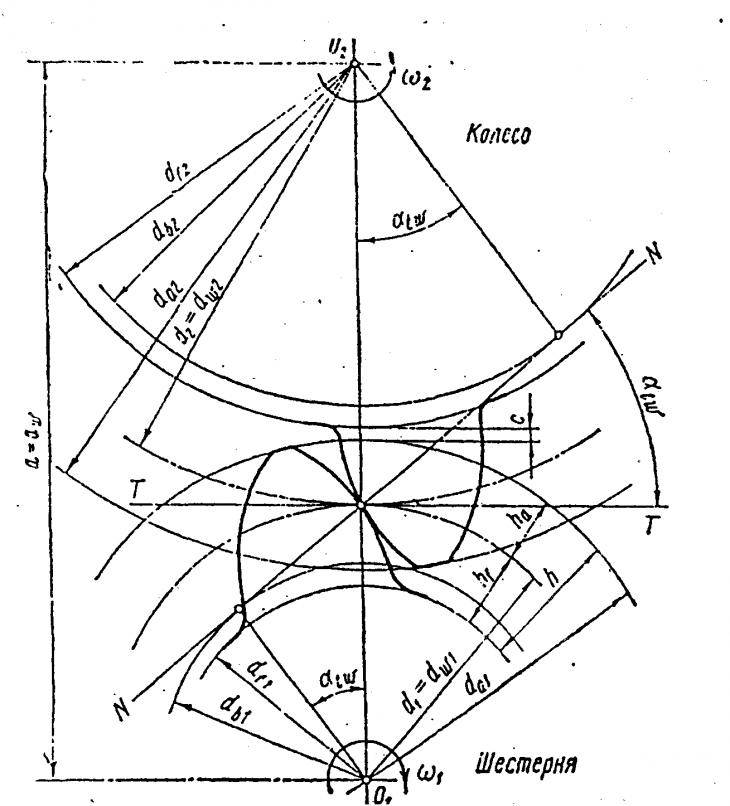
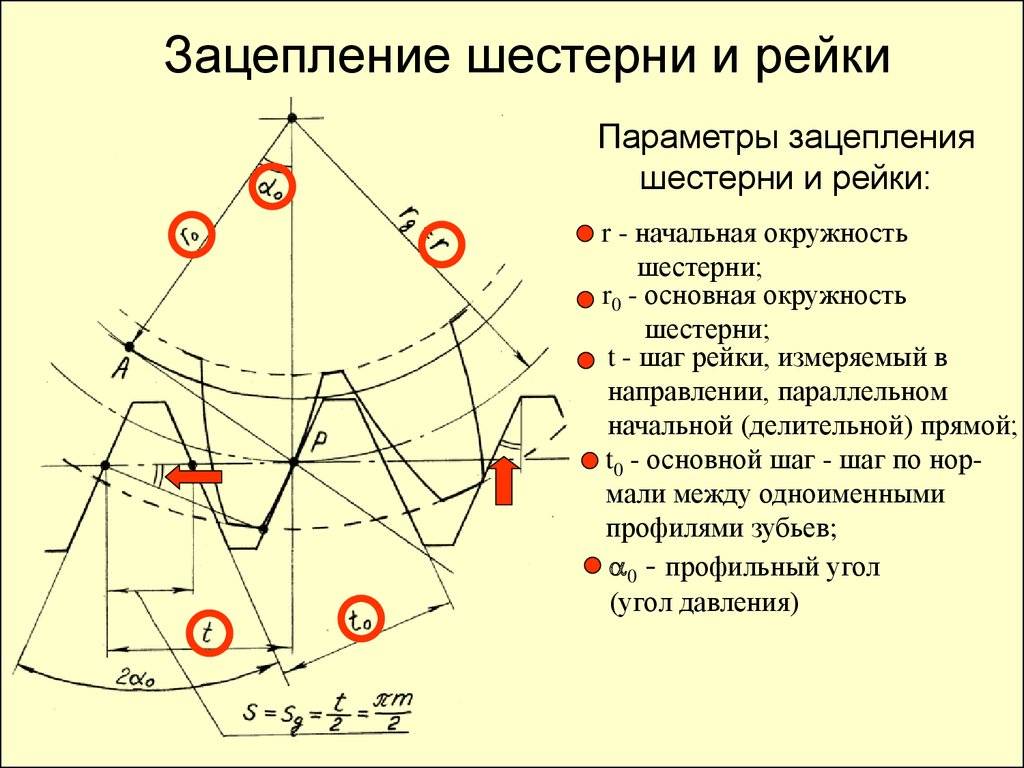
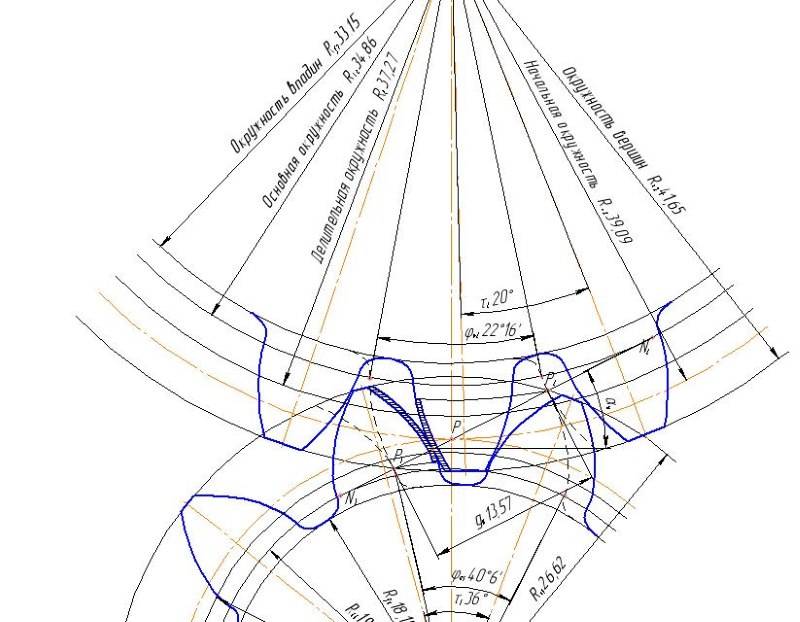
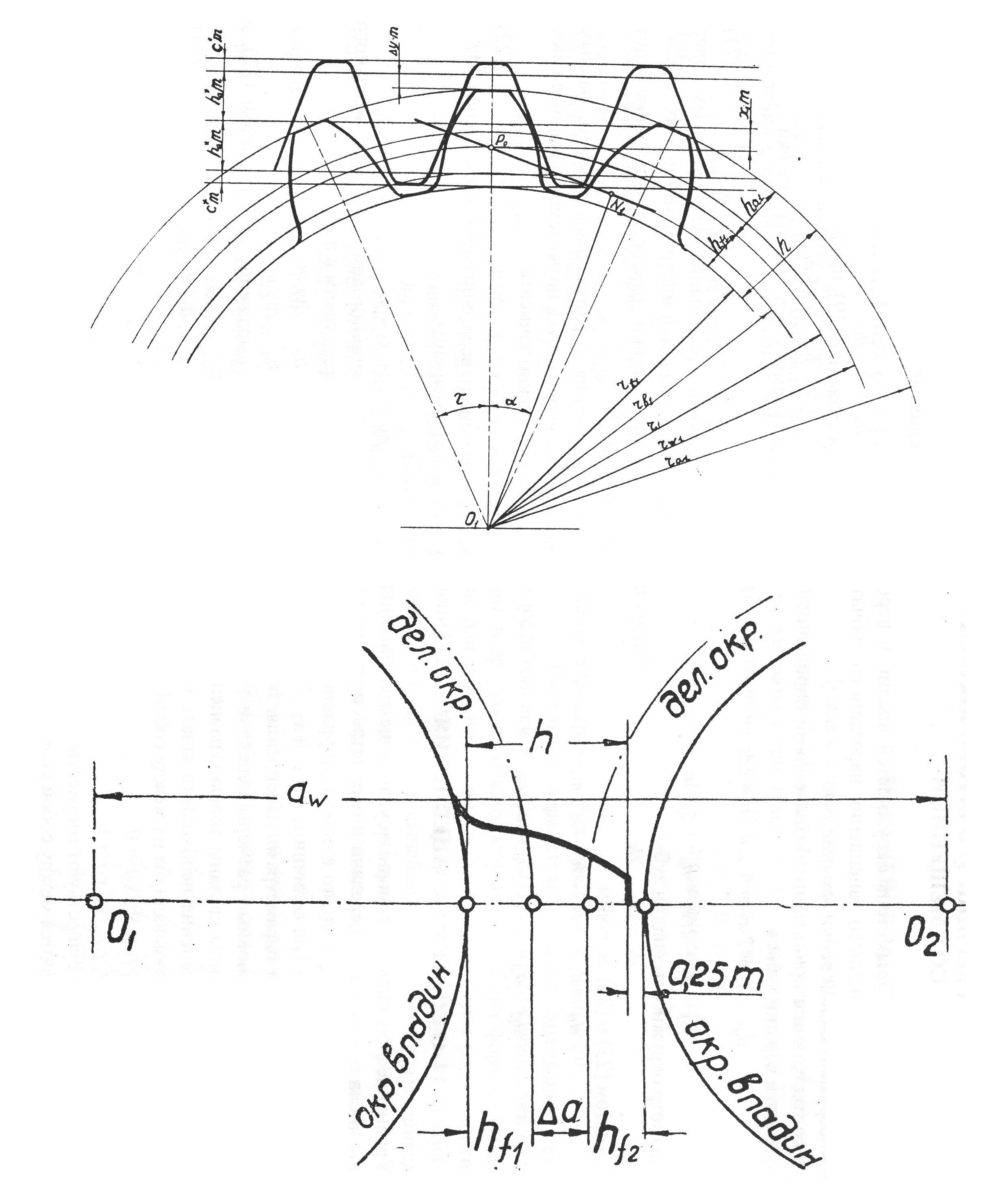
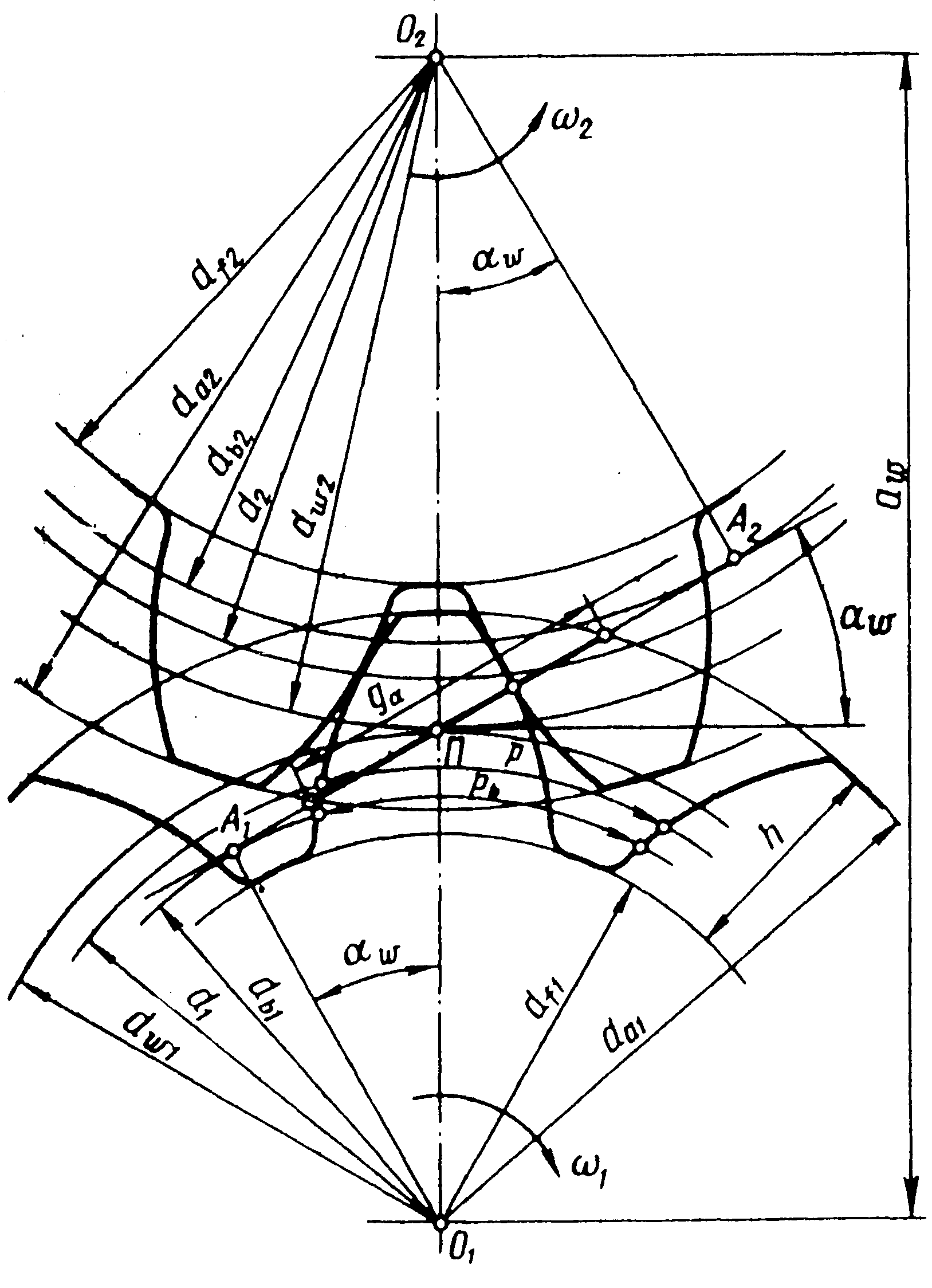
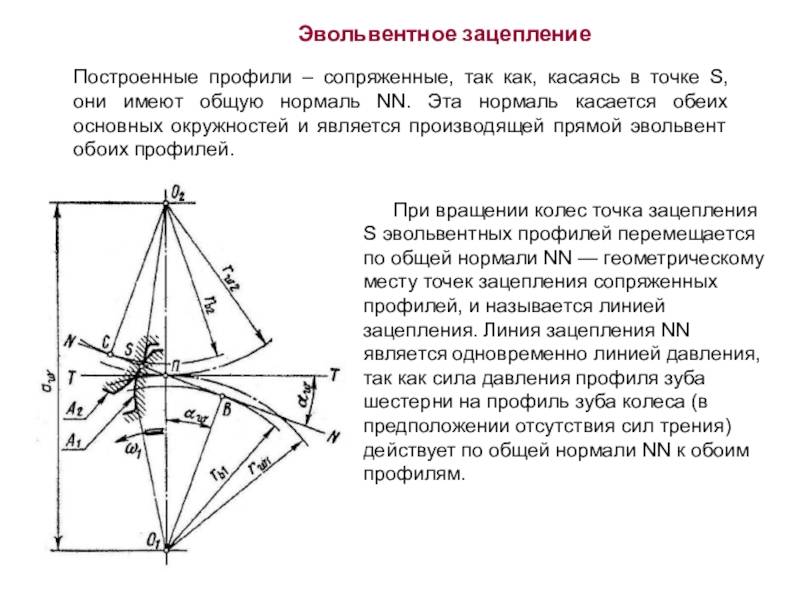
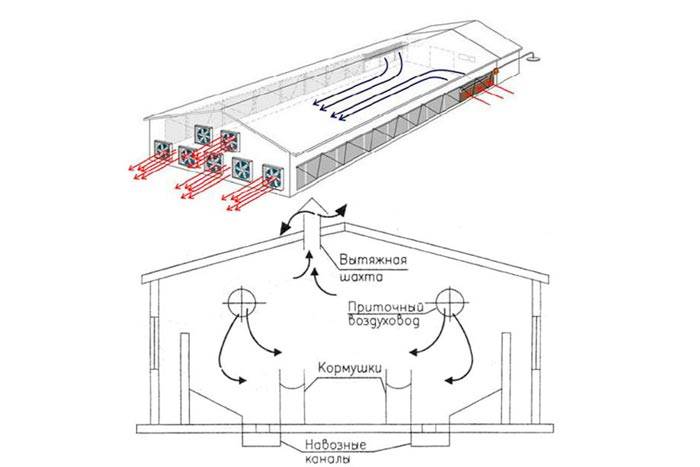
Схема наиболее распространенного наружного зубчатого зацепления в торцевом сечении показана на рисунке, расположенном ниже этого текста.
Исходные данные записываем в ячейки со светло-бирюзовой заливкой. В ячейки с бледно-голубой заливкой вносим исходные данные, внимательно выполнив требования, помещенные в расположенной над ними строке! Результаты расчетов считываем в ячейках со светло-желтой заливкой. В ячейках со светло-зеленой заливкой, как обычно, помещены мало подверженные изменениям исходные данные.
Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Коэффициент запаса прочности при работе зуба двумя сторонами
Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др. | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.
Вопросы для самопроверки
– Что называется зубчатым колесом?
– Назовите основные достоинства и недостатки зубчатых передач?
– Каково взаимное расположение геометрических осей колес в цилиндрических, конических и гиперболоидных передачах?
– Как различаются зубчатые передачи по расположению зубьев относительно образующей тела заготовки колеса?
– Чем отличаются внешнее, внутреннее и реечное зацепления?
– Назовите различие рядовой и планетарной передач?
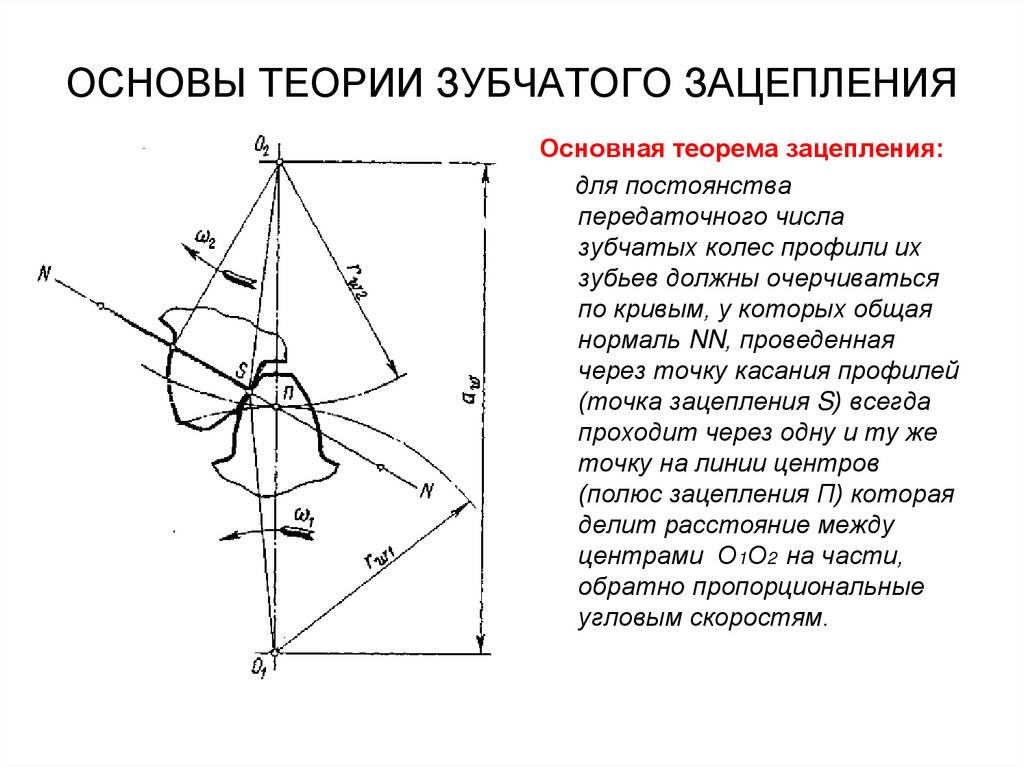
– В чем сущность основной теоремы зубчатого зацепления?
– Назовите элементы зубчатого колеса, какими линиями очерчивается профиль зуба?
– Назовите элементы зацепления пары колес.
– Что называется шагом колеса, модулем, головкой, ножкой зуба?
– Что такое полюс зацепления?
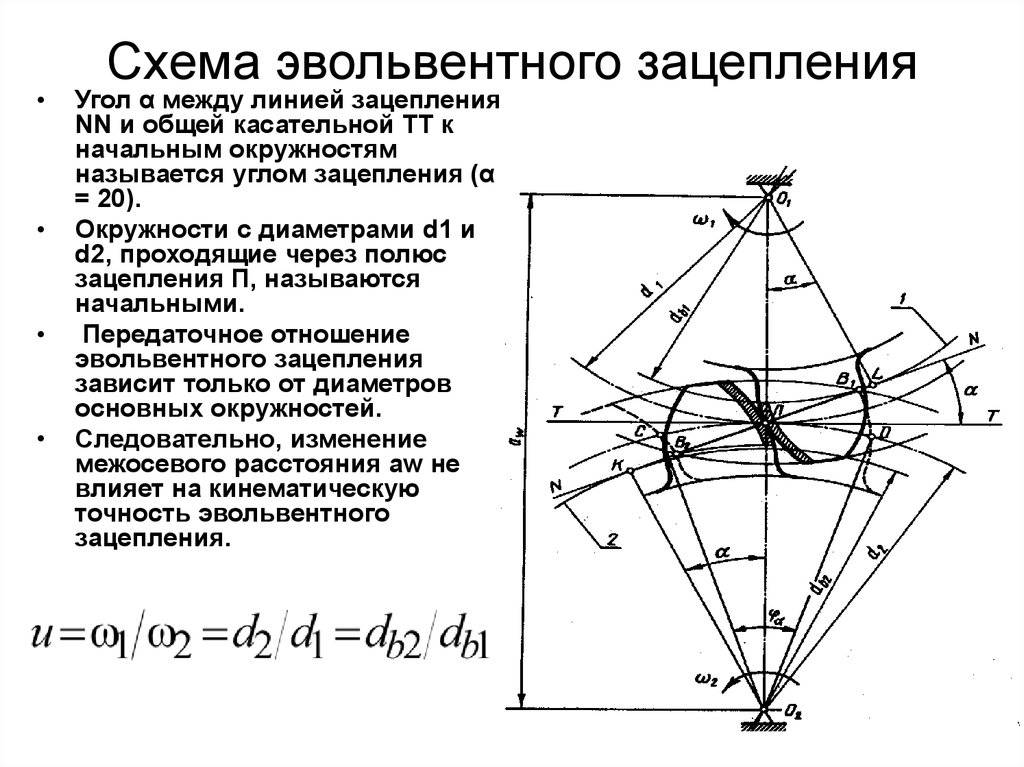
– Какой угол называется углом зацепления?
– Что такое линия зацепления, активная линия зацепления?
– Какая окружность колеса называется начальной окружностью?
– Какая окружность колеса называется основной?
– Какими свойствами обладает делительная окружность?
– Какие зубчатые колеса называются нулевыми, положительными и отрицательными?
– Что является центроидами относительного движения колес при постоянном передаточном отношении?
– Что такое удельное скольжение, почему возникает скольжение в контакте зубъев?
– Почему в полюсе зацепления удельное скольжение равно нулю?
– Происходит ли проскальзывание сопряженных профилей зубьев: в полюсе зацепления, в точках контакта, не совпадающих с полюсом?
– От чего зависит скорость относительного скольжения сопряженных профилей?
– На какой параметр работоспособности передачи влияет величина скорости скольжения?
– Что такое коэффициент удельного давления, где он применяется?
– Какие формы профиля зубьев отвечают основной теореме зубчатого зацепления?
– Дайте определение модуля зацепления.
– Что называется окружным шагом?
– Что такое передаточное число зубчатой передачи?
– Как определить передаточное отношение многоступенчатой зубчатой передачи?
– От чего зависит передаточное отношение рядовой передачи с последовательным соединением колес?
– Какая окружность зубчатого колеса называется делительной?
– Какая часть зуба называется головкой?
– Что такое коэффициент высоты головки зуба, чему он равен?
– Какая часть зуба называется ножкой?
– Могут ли два колеса, находящиеся в зацеплении иметь разный модуль?
– Какая окружность называется окружностью вершин?
– Какая окружность называется окружностью впадин?
– Чему равна высота головки зуба?
– Чему равна высота ножки зуба?
– Каково соотношение между высотой головки и и ножки зуба?
– В каком месте измеряется толщина зуба, ширина впадины колеса?
– Как рассчитать диаметр окружности вершин?
– Как рассчитать диаметр окружности впадин?
– Какая окружность называется эвольвентной?
– Какими свойствами обладает эвольвента окружности?
– Что такое эвольвентная функция?
– Назовите качественные характеристики эвольвентного зацепления?
– Какие профили зубъев колес называются сопряженными?
– Какими методами изготавливают эвольвентные зубъя, в чем заключается существо методов? Каковы основные достоинства и недостатки методов?
– Что такое реечный производящий исходный контур (инструментальная рейка)?
– Что такое коэффициент перекрытия? Каково его минимальное значение, необходимое для нормальной работы передачи?
– Для чего назначаются коэффициенты смещения при нарезании зубчатых колес?
– Какое число зубъев считается минимальным, от чего оно зависит?
– Чем определяется наименьшее число зубьев, обеспечивающее нормальную работу передачи?
– Что такое подрез зубчатого колеса?
– Как предотвратить подрез зубчатого колеса?
– Что такое коэффициент смещения исходного контура?
– Как изменится межосевое расстояние зубчатой передачи, если оба колеса имеют положительную коррекцию?
– Дайте определения окружного и углового шага эвольвентного зацепления.
– Запишите формулу для толщины зуба по окружности произвольного радиуса.
– Какие методы изготовления эвольвентных зубчатых колес Вы знаете ?
– В чем заключается сущность изготовления эвольвентных колес методом огибания ?
– Выведите основные размеры зубчатого колеса (ra, s,h), используя схему станочного зацепления.
– Запишите условие отсутствия подрезания в станочном зацеплении.
– Что такое x min ? Выведите формулу для определения x min.
– Запишите формулу для определения угла зацепления эвольвентной зубчатой передачи.
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Строительная механика
00:00:00
Эскизирование детали типа «колесо зубчатое»
Последовательность выполнения эскизов зубчатого колеса:
1. Внимательно осмотреть зубчатое колесо, изучить его конструкцию, назначение, технологию изготовления.
2. Определить минимальное, но достаточное количество изображений (видов, разрезов, сечений), необходимых для полного представления о конструкции детали. Ознакомиться с правилами изображения зубчатого колеса данного вида согласно требованиям соответствующих стандартов.
3. Избрать согласно ГОСТ 2.301-68 формат чертежа, начертить на нем рамку и основную надпись.
4. Наметить тонкими сплошными линиями габаритные прямоугольники для будущих изображений с учетом равномерного использования площади листа. Провести осевые линии.
5. Обозначить тонкими сплошными линиями видимый контур детали, начиная с основных геометрических форм и сохраняя на всех изображениях проекционную связь и пропорцию элементов детали.
6. Нанести выносные и размерные линии, стрелки, проставить необходимые знаки. Провести замеры зубчатого колеса и вписать размерные числа, причем размерные числа записывать сразу после каждого измерения, не накапливая их в памяти.
7. Заполнить основную надпись и записать технические требования.
8. Внимательно проверить эскиз зубчатого колеса и исправить ошибки.
При эскизировании зубчатого колеса необходимо правильно изобразить и поставить размеры не только на элементах зубчатого зацепления, но и на конструктивных элементах соединения колеса с валом. Для этого необходимо знать не только элементы зубчатого зацепления, но и иметь представления о креплении зубчатого колеса на вале.
Зубчатые передачи используются как самостоятельные агрегаты (редукторы) или входят в другие машин как составные части.
Для передачи вращательного движения с одного вала на другой, оси которых параллельные, применяют цилиндрические передачи (рис. 5.15, а, б, в, г); если оси валов пересекаются, используют конические передачи (рис. 5.15, д, е).
Если оси валов скрещиваются (чаще под прямым углом), применяют червячные передачи (рис. 5.15, з). Для преобразования вращательного движения в поступательное и наоборот применяют реечные передачи, которые состоят из цилиндрического колеса и рейки (рис. 5.15, и). Встречаются передачи с внешним и внутренним зацеплениями (рис. 5.15, г). В первом случае вращение колес происходит в противоположных направлениях, во втором – в одном направлении.
Рисунок 5.15
Зубчатое колесо содержит зубчатый венец и тело колеса. Зубья колеса образовывают зубчатый венец. Тело колеса ограничивается поверхностью впадин зубьев.
При изображении цилиндрических зубчатых колес приняты такие условности:
1. Поверхность вершин и ее образующую изображают сплошной основной линией, а поверхность впадин и ее образующую – сплошной тонкой линией. Делительную окружность изображают штрихпунктирною тонкой линией.
2. Зубья чертят только в осевых разрезах, изображая их не рассеченными. Если надо показать профиль зуба, то оформляют это выносными элементом или изображают его на ограниченном участке детали.
На рис. 5.16 изображены основные элементы зубчатого колеса.
Рисунок 5.16
Согласно ГОСТ 16531-83 основные параметры зубчатого колеса:
1) диаметр делительной окружности d
2) модуль m
– число, которое показывает, сколько миллиметров диаметра делительной окружности приходится на один зуб (количество зубьевz ):
Величины модуля стандартизированы (табл. 5.11).
Таблица 5.11 – Модули, мм ( ГОСТ 9563-60)
| 1-й ряд | 1,25 | 2,5 | |||||
| 2-й ряд | 1,125 | 1,375 | 2,25 | 2,75 | 3,5 | 4,5 | 5,5 |
С помощью параметров, приведенных в табл. 5.12, можно рассчитать величины, которые характеризуют зацепление.
Таблица 5.12 – Параметры цилиндрического зубчатого колеса
| Параметр зубчатого колеса | Обозначение | Величина, мм |
| Высота головки зуба | ha | ha = m |
| Высота ножки зуба | hf | hf = 1.25 m |
| Высота зуба | h | h = 2.25 m |
| Диаметр делительной окружности | d | d = m Z |
| Диаметр окружности выступов | da | da = d + 2 ha |
| Диаметр окружности впадин | df | df = d – 2 hf |
Используя эти соотношения, можно вычислить значение модуля для реального цилиндрического колеса:
В учебных целях добытое значение необходимо округлить к ближайшему по ГОСТ 9563-60.
Расстояние между одноименными профильными поверхностями соседних зубьев, измеренное в миллиметрах по дуге делительной окружности, называют шагом зацепления Pt.
Из рисунка видно, что шаг равняется соотношению длины делительной окружности к числу зубьев:
Параметры зубчатых колес задают на чертежах в специальных таблицах (ГОСТ 2.403-75).
На рис. 5.17 показано расположения и размеры таблицы параметров.
Рисунок 5.17
В случае необходимости отдельные строки из нее можно опускать. Пример выполнения чертежа колеса зубчатого (для учебных целей) приведен на рис. 5.18.
Рисунок 5.18
d3 = cos ? * D
От автора. Я нашел в интернете полезную программку в Excel 2007. Это автоматизированная табличка для расчета всех параметров прямозубого зубчатого колеса.
Скачать Скачать с зеркала
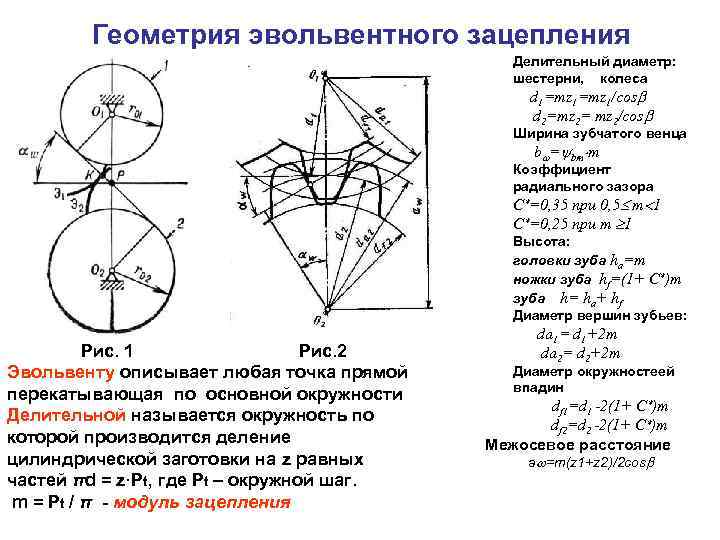
Итак, приступим к графическому построению профиля зубчатого колеса
- Изобразите делительный диаметр с диаметром D, и центром шестерни O. Окружность показана красным цветом.
- Изобразите диаметр вершин зубьев (d1) с центром в точке O с радиусом большим на высоту головки зуба(зелёного цвета).
- Изобразите диаметр впадин зубьев (d2) с центром в точке O с радиусом меньшим на высоту ножки зуба (голубого цвета цвета).
- Проведите касательную к делительному диаметру (желтая).
- В точке касания под углом ? проведите линию зацепления, оранжевого цвета.
- Изобразите окружность касательную к линии зацепления, и центром в точке O. Эта окружность является основной и показана тёмно синего цвета.
- Отметьте точку A на диаметре вершин зубьев.
- На прямой соединяющие точки A и O отметьте точку B находящуюся на основной окружности.
- Разделите расстояние AB на 3 части и отметьте, точкой C, полученное значение от точки A в сторону точки B на отрезке AB.
- От точки C проведите касательную к основной окружности.
- В точке касания отметьте точку D.
- Разделите расстояние DC на четыре части и отметьте, точкой E, полученное значение от точки D в сторону точки C на отрезке DC.
- Изобразите дугу окружности с центром в точке E, что проходит через точку C. Это будет часть одной стороны зуба, показана оранжевым.
- Изобразите дугу окружности с центром в точке H, радиусом, равным толщине зуба (s). Место пересечения с делительным диаметром отметьте точкой F. Эта точка находится на другой стороне зуба.
- Изобразите ось симметрии проходящую через центр О и середину расстояния FH.
- Линия профиля зуба отображенная зеркально относительно этой оси и будет второй стороной зуба.
Вот и готов профиль зуба прямозубого зубчатого колеса. В этом примере использовались следующие параметры:
- Модуль m=5 мм
- Число зубьев z=20
- Угол профиля исходного контура ?=200
Расчетные данные:
- Делительный диаметр D=100 мм
- Диаметр вершин зубьев d1=110 мм
- Диаметр впадин зубьев d2=87.5 мм
- Толщина зубьев по делительной окружности S=7.853975 мм
На этом первая часть урока является завершенной. Во второй части (видео) мы рассмотрим как применить полученный профиль зуба для построения модели зубчатого колеса. Для полного ознакомления с данной темой («зубчатые колеса и зубчатые зацепления», а также «динамические сопряжения в SolidWorks») необходимо вместе с изучением этого урока изучать урок №24.
Еще скажу пару слов о специальной программе, производящей расчет зубчатых колес и генерацию модели зубчатого колеса для SolidWorks. Это программа Camnetics GearTrax.
P.S.(16.03.2010) Скачать Camnetics GearTrax
А теперь переходим с следующей части урока.
Скачать 2-ю часть урока №30 Скачать с зеркала
/strong
Характеристики шлицевых соединений
По своей конструкции и способу передачи вращательного момента, шлицевые соединения можно отнести к многошпоночным. Несколько плоскостей взаимодействия при вращении, только вместо большого количества пазов и шпонок в них, только шлицевый вал и втулка. Шпонки отсутствуют, их заменяют шлицевые пазы и зубья, вырезанные непосредственно на сопрягаемых деталях. Конструкция позволяет значительно сократить погрешность изготовления и дает возможность перемещаться втулке вдоль оси вала, не прекращая радиальное движение.
Размеры шлицов определяются внутренним диаметром вала, их количеством и формой. В шлицевом соединении образуется несколько плоскостей контактов. Возможность передачи большого крутящего момента возрастает по сравнению со шпонками в несколько раз.
Зуб шлица нарезается фрезами на зуборезных станках и протяжкой. Для подвижных узлов делается последующая шлифовка боковых поверхностей. Длина зубьев может быть любой, у неподвижных шлицевых соединений равна высоте ступицы колеса. При скольжении шестерни вдоль оси, длина нарезанных выступов на валу определяется размером перемещения шестерни, ее высотой и технологическим припуском, равным радиусу фрезы для ее выхода при обработке.
Диаметр вала по наружной поверхности равен размеру втулки по впадинам. Втулка со шлицами в точности копирует своим отверстием профиль вала и плотно надевается на него. Шлицевые канавки по отверстию нарезаются на долбежном станке. Технология изготовления длительная, требует большой точности, которую не может обеспечить долбяк, поскольку длина резца большая относительно его сечения. При попытке ускорить обработку, сделать больше заход и подачу, инструмент отжимает, размер получается в минус.
При проектировании узла и подборе пар, основным параметром является внутренний диаметр по шлицам. Его рассчитывают на кручение и изгиб. Шлицевая втулка подвергается меньшим по силе воздействиям. Она выбирается по справочнику. Детали делают из среднеуглеродистых малолегированных сталей: Ст 45, Ст40Х, Ст 40ХН. Они имеют относительно высокую вязкость и низкую хрупкость в нормализованном состоянии и после объемной закалки на воздух при твердости 320–350 HB.
Определить количество зубьев при проектировании можно по таблицам. Они разделены для каждого внутреннего диаметра на 3 группы по нагрузкам:
- легкая;
- средняя;
- тяжелая.
Чем больше крутящий момент нужно передавать, тем выше сам шлиц и больше их количество. За счет этого увеличивается площадь контакта.
Зубчатые соединения рассчитываются с учетом погрешности изготовления. Между поверхностями сопряженных деталей имеется зазор соединения. При повороте ведущей детали он смещается в противоположную сторону от направления действия силы. В идеале все поверхности соприкасаются и нагружены одинаково. По факту зубчатые соединения изготавливаются с погрешностью в 0,01–0,03 мм, в зависимости от размера и способа обработки. Муфта одной плоскостью соприкасается сильнее, другими меньше. При расчете прочности выбирается по таблице поправочный коэффициент, позволяющий рассчитать параметры деталей на прочность с учетом неравномерных сил нагрузок.
Зазор в соединении определяет размер холостого хода. Начиная двигаться, ведущая деталь сначала выбирает просвет между рабочими плоскостями, затем начинается силовое воздействие и вращение ведомой детали и всего узла.
Проектирование цилиндрических зубчатых зацеплений
Перед тем как проектировать зубчатое колесо в Инвенторе, пользователь должен определиться с задачей, которую нужно решить. Генератор компонентов передачи выполняет следующие операции:
- произвести расчет геометрических и прочностных характеристик зубчатых зацеплений;
- вставить в сборку модель только одного или сразу двух зубчатых колес одного зацепления;
- добавить элемент зубчатого венца к существующей детали.
Другими словами, можно использовать генератор как исключительно расчетную систему или как средство для проектирования и построения трехмерных моделей шестерен. Кнопка запуска генератора находится на ленте на вкладке «Проектирование».
В окне генератора на вкладке «Модель» определяются и вычисляются геометрические параметры зацепления:
«Выбор модели». С помощью выпадающего списка определите параметры, по которым будет рассчитываться геометрия зацепления. Для расчета доступны варианты «Модуль и количество зубьев», «Количество зубьев», «Межосевое расстояние», «Общий коэффициент смещения» и «Модуль». Каждый тип расчета дает возможность ввести известные значения и с их учетом вычислить все остальные. Например, если известно межосевое расстояние между колесами, необходимо выбрать соответствующий пункт меню.
Поля «Передаточное отношение», «Модуль» и «Межосевое расстояние» предназначены для ввода соответствующих величин
Обратите внимание, что выбранный ранее вариант расчета определяет доступность определенных параметров для редактирования.
«Угол наклона зуба». Изменение угла наклона зуба позволяет проектировать косозубые цилиндрические колеса
Пользователь может ввести угол наклона в пределах от 0 до 55 градусов с возможностью изменения направления угла.
Определите параметры для зубчатого колеса 1. В выпадающем списке выберите «Компонент», если необходимо вставить модель колеса в сборку, «Элемент», если нужно добавить к существующей детали зубчатый венец, или «Без модели», если построение не требуется. Для точного позиционирования модели укажите цилиндрическую грань, к оси которой она будет привязана, начальную плоскость и ширину шестерни. Также, если необходимо, укажите количество зубьев.
Аналогично определите параметры для зубчатого колеса 2.
После ввода всех требуемых параметров нажмите кнопку «Расчет». Программа вычислит недостающие значения и выдаст отчет о результатах. Если при расчете возникнут ошибки, то область отчета выделится красным цветом, а в самом отчете выведется информация о найденных ошибках. Путем корректировки исходных данных нужно добиться окончательного правильного расчета, а синее выделение области отчета будет сигнализировать о правильных результатах.
При необходимости выполнения расчета на прочность перейдите на вкладку «Расчет» и задайте следующие параметры:
- «Метод расчета прочности». Из списка вариантов выберите необходимую методику. Для выбора доступны расчеты по стандартам ANSI, ISO, DIN и CSN.
- «Нагрузка». Определите величины нагрузок на зубчатые колеса: мощность, скорость вращения, крутящий момент и КПД.
- «Характеристики материалов». Материал колес можно выбрать из предложенных или самостоятельно ввести характеристики.
- «Требуемый срок службы». Введите расчетный срок службы передачи в часах.
После нажатия кнопки «Рассчитать» система вычислит необходимые значения и сформирует отчет. Если в результате вычислений какие-то параметры выйдут за допустимые пределы, то в отчете они выделятся красным цветом. Для устранения ошибок откорректируйте входные данные или измените геометрию элементов зубчатого зацепления.
Если на вкладке «Модель» было определено, что необходимо построить компоненты или элементы колес, то после нажатия кнопки «ОК» в модели появятся компоненты зубчатой передачи, а в браузере модели появится новый элемент «Цилиндрическое зубчатое зацепление».
Важно! Созданные компоненты передачи представляют из себя обычные детали, не связанные сборочными зависимостями с остальными элементами сборки. Чтобы отредактировать параметры элементов передачи необходимо кликнуть правой кнопкой мыши на зацеплении в браузере и в контекстном меню выбрать «Редактировать с помощью генератора»
Чтобы отредактировать параметры элементов передачи необходимо кликнуть правой кнопкой мыши на зацеплении в браузере и в контекстном меню выбрать «Редактировать с помощью генератора».
Построение эвольвентного зацепления
Существует несколько способов построения эвольвентного зацепления, используемого для изготовления зубчатых колес, которые можно выполнять вручную или с помощью систем автоматического построения.
При проектировании зацепления зубчатых колес учитывают не только геометрические параметры, но и технологические процесс изготовления, а также желаемые динамические и прочностные показатели готового механизма.
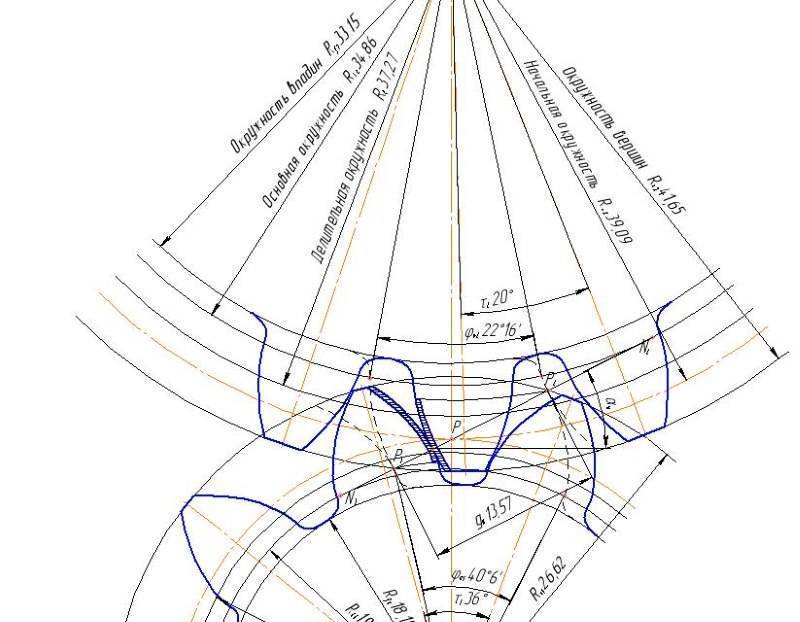
Построение эвольвенты зубчатого колеса состоит из нескольких этапов:
- Графическое построение окружности радиусов (определяется исходя из необходимого количества зубьев и прочностных характеристик готового механизма).
- Через полюс зацепления проводится прямая в токе касания изначальных окружностей (строится под необходимым углом зацепления).
- Окружности колес должны соприкасается по полученной прямой. Обкатывание ее по окружности первого колеса, точка, совпадающая с полюсом, образует первую эвольвенту. Такая же манипуляция с колесом 2, позволяет получить вторую эвольвенту.
При производстве шестерен зубья несколькими методами: копирования и обкатки. Если необходимо изготовить мелкую деталь, прибегают к методу формообразования, другими словами – горячей накатки. Такой способ менее точен, но форма фрезы при копировании не позволяет выполнить миниатюрные вырезы.
Метод копирования предусматривает вращение фрезы вдоль поверхности, образующее зубья. Она прорезает одну впадину за один проход между соседними зубьями. Затем фреза возвращается в базовое положение с одновременным поворотом заготовки на необходимый угол шага. Такой способ изготовления довольно точный, но производительность его низкая.
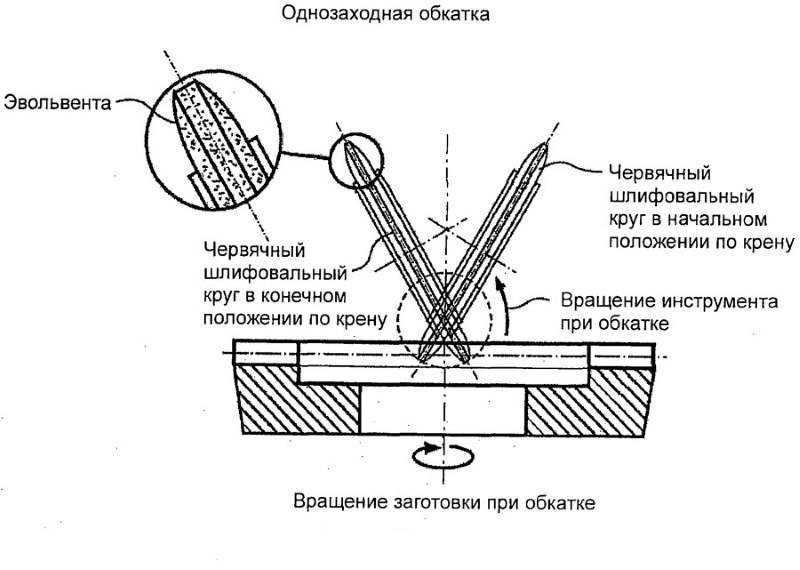
Более совершенным способом является метод обкатки. В его основе лежит огибающее движение, соответствующее желаемому движению зубчатого колеса при зацеплении. Процесс производства похож на движение шестерен в работе. Такое зацепление называется станочным. Рабочий инструмент в таком случае изготавливается в виде круглой, зубчатой фрезы или инструментной рейки.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
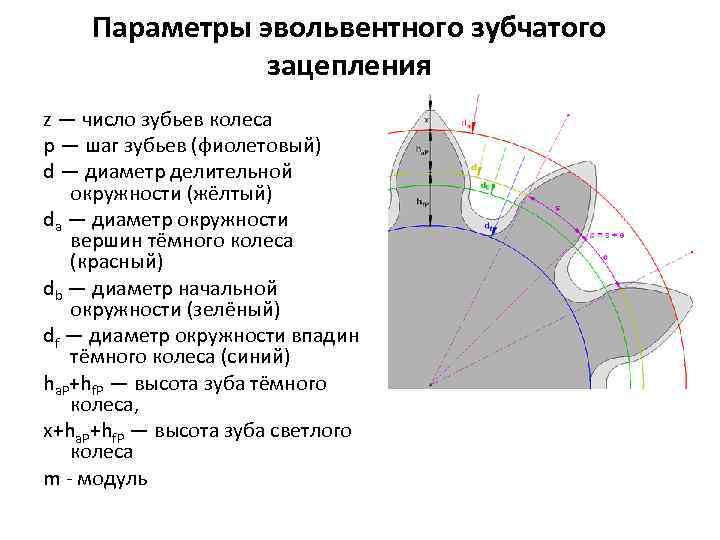
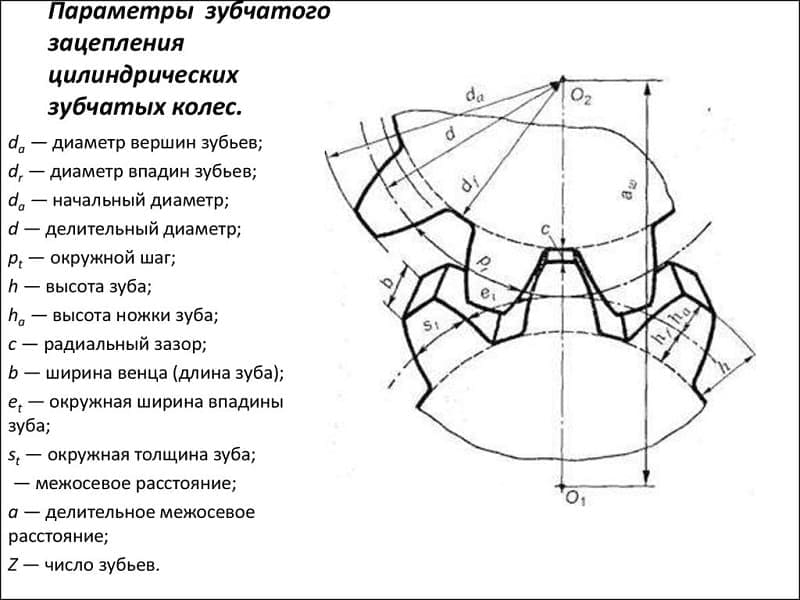
Основные параметры зубчатого колеса
Создавать рассматриваемую конструкцию следует исключительно при заблаговременном создании чертежа, на котором отображаются основные параметры зубчатого колеса. Стоит отметить, что по создаваемой схеме некоторых механизмов также можно определить неправильный выбор основных параметров. В большинстве случае также делается упрощенный чертеж вала, за счет чего можно сразу определить принцип действия механизма.
Основными параметры, которые относятся к зубчатым колесам, являются:
- Делительная окружность пары зубчатых колес. Данный показатель применяется в случае проектирования зубчатой пары самого различного типа. Она определяется соприкасающимися окружностями, которые катаются одна по другой без скольжения. Применяется для обозначения момента зацепления и сопряжения. Для обозначения на чертеже применяется буква d. Стоит учитывать, что само обозначение зачастую не проставляется, а только указывается соответствующий размер.
- Окружный шаг зубьев. Этот параметр применяется для определения расстояния между отдельными профильными поверхностями соседних зубьев. Подобный показатель вычисляется путем разделения значения делительной окружности на число зубьев.
- Число зубьев. Достаточно важным моментом назовем то, что на чертеже не проводится отображение всех зубьев. В некоторых случаях проводится создание эскиза нескольких зубьев. За счет этого существенно упрощается поставленная задача по созданию рассматриваемого документа.
- В создаваемой таблице в обязательном порядке указывается число зубьев. Подобная информация позволяет проводить расчеты и определение других наиболее важных параметров.
- Длина делительной окружности.
- Основные геометрические параметры зуба. Основной частью зубчатых колес является именно зуб. Он применяется
Если не учитывать основные параметры, то есть вероятность быстрого износа поверхности и появления многих других проблем.
Расчет в Excel координат точек профиля зуба.
Для выполнения громоздких и достаточно сложных расчетов запускаем программу MS Excel. Выполнить этот расчет можно и в программе Calc из бесплатных офисных пакетов Apache OpenOffice или LibreOffice.
Представленный далее алгоритм расчета адаптирован для колес с наружными зубьями. Для колес с внутренними зубьями его можно применить после незначительных поправок.
Для косозубых колес профиль строится для торцевого сечения.
Исходные данные:
Профиль зуба будем «нарезать» реечным инструментом – гребенкой или червячной фрезой. Параметры и коэффициенты исходного контура возьмем по ГОСТ13755-81. Посмотреть на чертеж исходной рейки и понять, что это такое можно здесь.
Первые четыре параметра в ячейках D3-D6 характеризуют исходный контур.
Следующие пять исходных данных в ячейках D7-D11 являются «паспортом» зубчатого колеса, представляя о нем исчерпывающую информацию.
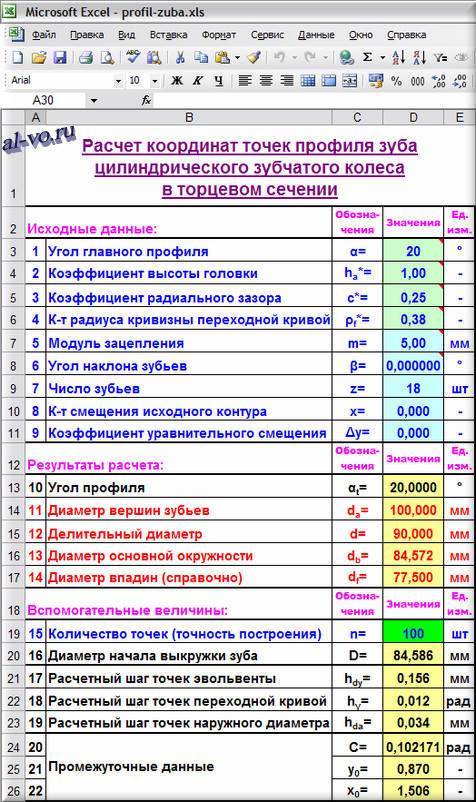
Алгоритм расчетов:
Результаты расчетов угла профиля и всех диаметров получены по следующим формулам:
10. αt=arctg (tg (α)/cos (β))
11. dа=d+2*m*(ha*+x— Δy)
12. d=m*z/cos (β)
13. db=d*cos (αt)
14. df=dа-2*m*(2*ha*+c*— Δy)
Часть профиля зуба – это эвольвента основной окружности диаметром db. Таким образом, эвольвента может существовать в зубчатом колесе от диаметра основной окружности до диаметра вершин зубьев!
Вторая часть профиля зуба – переходная кривая от эвольвенты до диаметра впадин.
Я выбрал количество точек n каждой из кривых для своего примера равное 100, посчитав его достаточным для требующейся точности построения. Если вы захотите его изменить, то вам нужно будет соответственно расширить или сузить таблицу «Координаты точек профиля зуба», которая сдержит 100 строк (imax=n).
Результаты вспомогательных констант определены по формулам:
16. D=2*m*((z/(2*cos (β)) — (1-x))2+((1-x)/tg (αt))2)0,5
17. hdy=(da–db)/(n-1)
18. hγ=γ1/(n-1)
19. hda=2*Xэ1/(n-1)
20. C=(π/2+2*x*tg (α))/z+tg (αt) — αt
21. y0=1- (ρf*)*sin (αt) –x
22. x0=π/(4*cos (β))+(ρf*)*cos (αt)+tg (αt)
Подготовка завершена, можно выполнить расчет в Excel промежуточных данных и непосредственно координат точек профиля зуба.
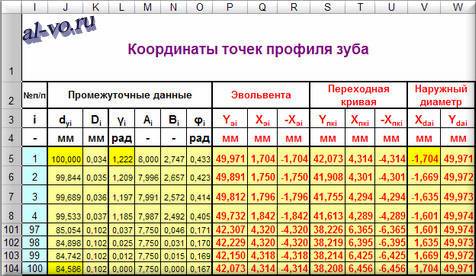
Значения в таблице рассчитаны по формулам:
dy1=da
dy (i+1)=dyi–hdy
dy (n)=db
Di=arccos (db/dyi) -tg (arccos (db/dyi))+C
γ1=π/2- αt
γ (i+1)=γ i–hγ
Ai=z/(2*cos(β)) – y0— (ρf*)*cos (γ i)
Bi=y0*tg(γ i))+(ρf*)*sin (γ i)
φi=(2*cos(β)/z)*(x+y0*tg (γ i))
Yэi=(dyi/2)*cos (Di)
Xэi=Yэi*tg (Di)
Yпкi=(Ai*cos (φi)+Bi*sin (φi))*m
Xпкi=(Ai*sin (φi) -Bi*cos (φi))*m
Xda1=-Xэ1
Xda (i+1)=Xdai+hda
Ydai=((dа/2)2— Xdai2)0,5
После того, как расчет в Excel выполнен, запускаем мастера диаграмм и строим точечные графики по полученным координатам. О том, как это делается подробно описано тут.
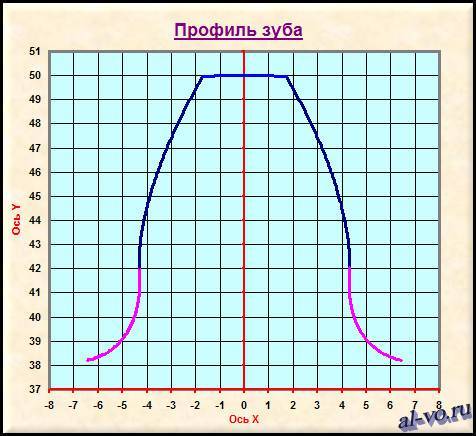
На скриншоте выше синим цветом показан наружный диаметр, темно-синим изображены эвольвенты, лиловым – переходные кривые.
Оси X и Y пересекаются в центре колеса — это точка начала координат.
Excel построил профиль зуба! Задача решена.
Изменяя исходные данные можно мгновенно оценить визуально изменения профиля зуба и увидеть подрезку ножки или заострение вершины при применении смещения контура.
Итоги.
Для того чтобы начертить полный реальный контур зубчатого колеса следует взять координаты точек профиля одного зуба и в любой доступной CAD-программе по этим точкам построить сплайн. Затем нужно размножить его по окружности на количество зубьев, достроить диаметр впадин и получить DXF-чертеж. Имея чертеж, легко написать управляющую программу для станка с ЧПУ и изготовить деталь.
Многие CAD-программы могут выдать чертеж контура зубчатого колеса и без описанных действий, но контур, к сожалению, в большинстве случаев не будет реальным!
Есть интересная программа Gear Template Generator, которая генерирует DXF-файлы контуров зубчатых колес (http://woodgears.ca/gear/index.html). Однако исходные данные для построений какие-то нетрадиционные… да и впадины зубьев — без радиального зазора.
Хочу отметить, что предлагаемый к скачиванию файл Excel с расчетами профиля зуба в данном случае не является полноценной программой и требует от пользователя при работе основополагающих знаний MS Excel и понимания геометрии задачи.
В частности, меняя исходные данные, придется вручную подстраивать шкалы осей и следить за тем, чтобы масштаб по оси X был равен масштабу по оси Y (сетка линий должна образовывать квадратики, а не прямоугольники). Точку сопряжения эвольвенты и переходной кривой при переносе координат в CAD-программу придется корректировать вручную, обрезая ненужные части кривых.
Представленный алгоритм был написан (страшно подумать) в 1992 году для программируемого калькулятора и предназначался для вычерчивания на кульмане чертежей контрольных экранов для оптико-шлифовальных станков.
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
Ссылка на скачивание файла с расчетами: profil-zuba (xls 107KB).